Bahupado Par Sankriyaen
बहुपदों पर संक्रियाएँ (Operation on Polynomial), बहुपदों का योग, बहुपदों का घटाव, बहुपदों का गुणा, और बहुपदों का भाग होती है।
- बहुपदों का योग
- बहुपदों का घटाव
- बहुपदों का गुणा
- बहुपदों का भाग
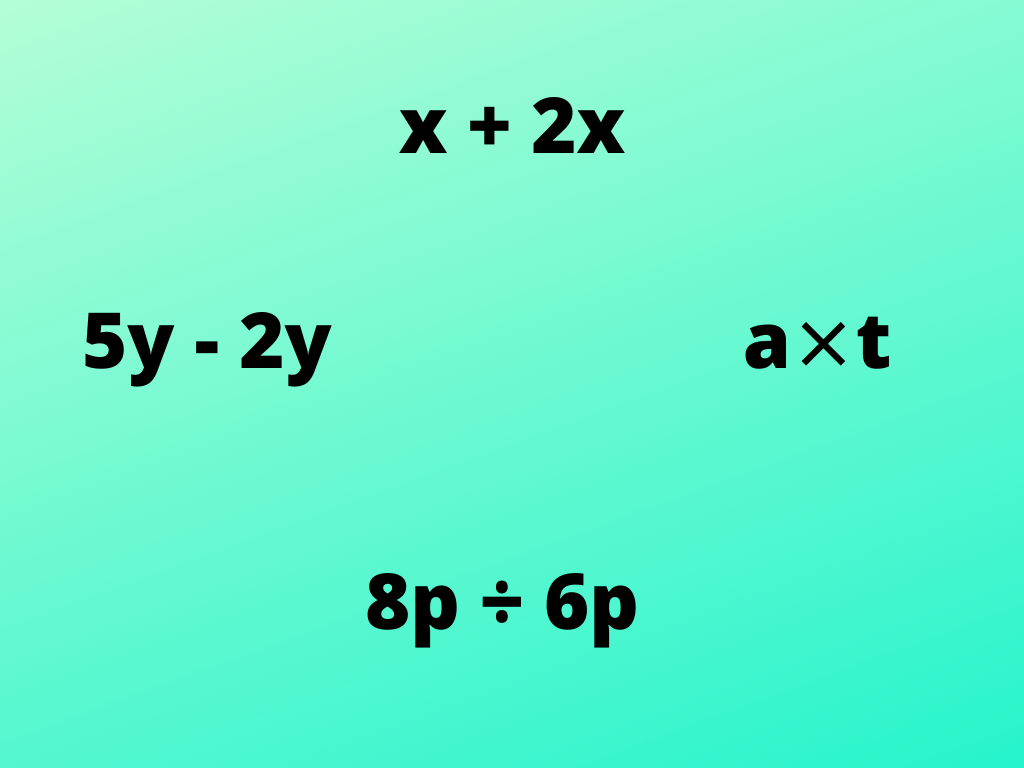
बहुपदों का योग
बहुपदो पर संक्रियाओं (Operation on Polynomial) में, जब हम दो या दो से अधिक बहुपदो को जोड़ते हैं तो केवल समान पद जोड़े जाते हैं इसका अर्थ है कि समान चर और समान घात वाले पद जोड़े जाते हैं। असमान पदों को नहीं जोड़ा जाएगा, वो अपरिवर्तित रहेंगे। जोड़ में, परिणामी बहुपद की घात समान रहती है।
उदाहरण – बहुपदो 3x2 + 4xy + 2y2 और 5y2 – xy + 7x2 को जोड़ें।
हल – 3x2 + 4xy + 2y2 + 5y2 – xy + 7x2
(3x2 + 7x2) + (4xy – xy) + (2y2 + 5y2)
10x2 + 3xy + 7y2 उत्तर
बहुपदो का घटाव
बहुपदों का घटाव बहुपदों के योग के समान ही होता है। इसमें समान पदों को घटाया जाता है और असमान पदों में कोई परिवर्तन नहीं होता है। इसमें भी परिणामी बहुपद की घात वही रहेगी।
उदाहरण – बहुपद 3xy2 + 4xy – 6x2y + y3 को 8xy2 + 7xy + x2y में से घटाएं।
हल – 8xy2 + 7xy + x2y – (3xy2 + 4xy – 6x2y + y3)
8xy2 + 7xy + x2y – 3xy2 – 4xy + 6x2y – y3
(8xy2 – 3xy2) + (7xy – 4xy) + (x2y + 6x2y) – y3
5xy2 + 3xy + 7x2y – y3 उत्तर
बहुपदों का गुणा
जब दो या दो से अधिक बहुपदों को गुणा किया जाता है तो परिणाम हमेशा उच्च घात वाला बहुपद होता है। लेकिन दो बहुपदों में, यदि एक या दोनों बहुपद अचर बहुपद हों तो घात वही रहेगी। बहुपदों के गुणा में, समान चरों की घातो को घातांक के नियमों द्वारा जोड़ा जाता है।
एकपदी को एकपदी से गुणा करना
दो एकपदी का गुणा करना
उदाहरण – 1) 4x⨯6y = (4⨯6)⨯(x⨯y) = 24xy
2) 3a⨯(-2b) = {3⨯(-2)}⨯(a⨯b) = -6ab
3) 6p2⨯8p = (6⨯8)⨯(p2⨯p) = 48p3
4) x4yz2⨯2xy3z = (1⨯2)⨯(x4⨯x⨯y⨯y3⨯z2⨯z) = 2x5y4z3 उत्तर
तीन या अधिक एकपदी का गुणा करना
उदाहरण – 1) 7t⨯2s⨯3r = (7⨯2⨯3)⨯(t⨯s⨯r) = 42tsr उत्तर
2) 4pq⨯5p2q2⨯6p3q3
= (4⨯5⨯6)⨯(p⨯p2⨯p3⨯q⨯q2⨯q3)
= 120p6q6 उत्तर
3) 2x2y⨯(-4y2z)⨯(-7z2x)⨯2x2yz
= [2x2y⨯(-4y2z)]⨯[(-7z2x)⨯2x2yz]
= (-8x2y3z)⨯(-14x3yz3)
= 112x5y4z4 उत्तर
एकपदी को बहुपद से गुणा करना
एकपदी को द्विपद से गुणा करना
उदाहरण – 1) 2a⨯(3b+4)
वितरण नियम का उपयोग करने पर,
= 2a⨯3b + 2a⨯4
= 6ab + 8a उत्तर
2) 7xy⨯(y2+5)
= 7xy⨯y2 + 7xy⨯5
= 7xy3 + 35xy उत्तर
एकपदी को त्रिपद से गुणा करना
उदाहरण – 1) 3v⨯(4v2+5v+7)
वितरण नियम का उपयोग करने पर,
= 3v⨯4v2 + 3v⨯5v + 3v⨯7
= 12v3 + 15v2 + 21v उत्तर
2) x2⨯(9xz+6y2-xyz)
= x2⨯9xz + x2⨯6y2 – x2⨯xyz
= 9x3z + 6x2y2 – x3yz उत्तर
बहुपद को बहुपद से गुणा करना
द्विपद को द्विपद से गुणा करना
उदाहरण – 1) (2x+3y)⨯(3x+2y)
= 2x⨯(3x+2y) + 3y⨯(3x+2y)
= 2x⨯3x + 2x⨯2y + 3y⨯3x + 3y⨯2y
= 6x2 + 4xy + 9xy + 6y2
= 6x2 + 13xy + 6y2 उत्तर
2) (p2-6qr)⨯(9q2+7r)
= p2⨯(9q2+7r) – 6qr⨯(9q2+7r)
= p2⨯9q2 + p2⨯7r – 6qr⨯9q2 – 6qr⨯7r
= 9p2q2 + 7p2r – 54q3r – 42qr2 उत्तर
द्विपद को त्रिपद से गुणा करना
उदाहरण – 1) (a+5)⨯(a2+2a-7)
= a⨯(a2+2a-7) + 5⨯(a2+2a-7)
= a⨯a2+a⨯2a-a⨯7 + 5⨯a2+5⨯2a-5⨯7
= a3+2a2-7a + 5a2+10a-35
= a3+7a2+3a-35 उत्तर
2) (x2-3)⨯(xy+yz+zx)
= x2⨯(xy+yz+zx) – 3⨯(xy+yz+zx)
= x2⨯xy+x2⨯yz+x2⨯zx – 3⨯xy – 3⨯yz – 3⨯zx
= x3y + x2yz + x3z – 3xy – 3yz – 3zx उत्तर
बहुपदों का भाग
बहुपद के विभाजन में, परिणाम कम घात वाला बहुपद होता है और यदि बहुपदों में से एक अचर बहुपद है तो घात वही रहेगी।
एकपदी को एकपदी से विभाजित करना
आसान विभाजन के लिए, हम इस प्रकार के विभाजन में भाज्य और भाजक दोनों का गुणनखंड करते हैं।
उदाहरण – 1) 6x4 ÷ 3x
= 2⨯3⨯x⨯x⨯x⨯x/3⨯x = 2⨯x⨯x⨯x = 2x3 उत्तर
2) 72p2q3r ÷ (- 6p4q)
= 2⨯2⨯2⨯3⨯3⨯p⨯p⨯q⨯q⨯q⨯r/-2⨯3⨯p⨯p⨯p⨯p⨯q
= 2⨯2⨯3⨯q⨯q⨯r/-p⨯p = 12q2r/-p2 उत्तर
बहुपद को एकपदी से विभाजित करना
उदाहरण – 1) (2xy + 6x) ÷ 2x
= (2xy + 6x)/2x = 2x(y + 3)/2x = (y+3) उत्तर
2) (8y3 + 6y2 + 12y) ÷ 2y
= (8y3 + 6y2 + 12y)/2y = 2y(4y2 + 3y+ 6)/2y
= 4y2 + 3y+ 6 उत्तर
इसे इस प्रकार भी हल किया जा सकता है = 8y3/2y + 6y2/2y + 12y/2y = 4y2 + 3y+ 6
बहुपद को बहुपद से विभाजित करना
उदाहरण – 1) (7a2 + 14a) ÷ (a + 2)
= (7a2 + 14a)/(a + 2) = 7a(a + 2)/(a + 2) = 7a उत्तर
2) (x4 – 5x3 – 24x2) ÷ x(x – 8)
= (x4 – 5x3 – 24x2)/x(x – 8) = x2(x2 – 5x – 24)/x(x – 8)
= x(x2 – 8x + 3x – 24)/(x – 8) [(x2 – 5x – 24) का गुणनखंड]
= x{x(x – 8) + 3(x – 8)}/(x – 8)
= x(x – 8)(x + 3)/(x – 8) = x(x + 3) उत्तर
यदि उपरोक्त विधि बहुपद को बहुपद से विभाजित करने में आपकी सहायता नहीं करती है, तो विभाजित करने की एक अन्य विधि भी है जिसे विभाजन एल्गोरिथ्म कहा जाता है।
बहुपदो पर संक्रियाएँ (Operation on Polynomial) कक्षा 10 अँग्रेजी में
बहुपदो पर संक्रियाएँ (Operation on Polynomial) के बारे में अधिक जानकारी






























































































































































![बहुपद के शून्यकों का ज्यामितीय (आलेखीय) अर्थ कक्षा 10 [Geometrical (Graphical) Meaning of the Zeroes of the Polynomial Class 10th]](https://mitacademys.com/wp-content/uploads/2022/07/बहुपद-के-शून्यकों-का-ज्यामितीय-आलेखीय-अर्थ.png)


