Introduction
A polynomial word is made up of two Greek terms “poly” which means many and “nominal” which means terms So, a polynomial means many terms. Polynomials are the combined expression of variables, constants, and exponents (only whole numbers) with arithmetic expressions like addition, subtraction, multiplication, and division (division by only constant terms).

Polynomials can have one variable and more than one variable with a finite number of terms.
Examples –
| (1) 3x | (6) 6zt – 7x + 8 |
| (2) 5x2 + 6x – 4 | (7) s3 + t5 – xy – 3 |
| (3) x4 – 9x + 8 | (8) 7x3 |
| (4) 7x3 + x2 – 2x + 1 | (9) 8xyz + y3 – t |
| (5) 9 | (10) x + y |
All the above examples are polynomials. A polynomial in one variable is denoted by p(x), g(x), f(a), q(y)…. etc. where the letter written in the bracket shows the variable of the polynomial.
If we take the example p(x) = 5x2 + 6x – 4, there are three terms in it.
Variable = x, Exponent term = x2, constant = 4, coefficient of x2 and x = 5 & 6
Terms – In the polynomial, terms are connected with the arithmetic operations of addition and subtraction.
Examples –
| Polynomials | Number of Terms |
|---|---|
| 7x3 + x2 – 2x + 1 | Four Terms |
| 8xyz + y3 – t | Three Terms |
| 3x | One Term |
| 9 | One Term |
Variable – Variables are unknown values that are denoted by the English alphabet. Like x, y, z, a, t….. etc.
Constants – Constants are the known numbers used in polynomials. It is real numbers. Like 5, 6, -8, -3, 1.4, 6.2, 1/3.…. etc.
Exponent – The number or alphabet which is continuously multiplied by itself can be written in the exponent form. Like x3, y5, z6…… etc.
Coefficient – The multiplication factor of any term is called the coefficient. Like coefficient of x2 in 5x2 is 5.
Types of Polynomials
Constant Polynomial – The polynomial which contains only a single constant value is called a constant polynomial.
Examples – 3, -8, 2, -9…..etc. 0 is called a zero polynomial.
Monomials – Polynomials having only one term are called monomials.
Examples – 3x, 7x4, 5, t7, – 9z2……etc.
Binomials – Polynomials having two terms are called binomials.
Examples – x + 8, y9 – z21, t8 + 9…….etc.
Trinomials – Polynomials having three terms are called trinomials.
Examples – 6zt – 7x + 8, 8xyz + y3 – t, x4 – 9x + 8……etc.
Degree of the Polynomials
When the polynomial is in one variable, then the highest power of the variable in the polynomial is called the degree of polynomials.
| POLYNOMIALS EXAMPLES | DEGREE | TYPE |
| 2(2x0), 4, 5, 9, | 0 | Constant polynomial |
| 5x, x + 7, 2x – 8 | 1 | Linear polynomial, General form p(x) = ax+b, a ≠ 0 |
| x2 – 3x + 2, 7y2 + y – 9, z2 + 6 | 2 | Quadratic polynomial, General form p(x) = ax2+bx+c, a ≠ 0 |
| t3 + t2 – t + 1, a3 – 2a, s3 + 7s2 + 8s + 9 | 3 | Cubic polynomial, General form p(x) = ax3+bx2+cx+d, a ≠ 0 |
What to do when more than one variable is present in the polynomial. Here is the example – Find the Degree of 7x2y + x2 + xy + 2
To find the degree, we add the powers (exponents) of variables of each term, then the highest power will be the degree of that polynomial.
In the above example, first term x2y = 2+1 = 3 there is power 1 on y, generally do not write.
Second term x2 = 2
Third term xy = 1+1 = 2
Fourth term 2 = 0 (no variable)
The highest power is 3 so the degree is 3.
- The Degree of a non-zero constant polynomial is zero.
- The degree of a zero polynomial is not defined.
- Polynomials having degree 1 are called linear polynomials. the maximum terms in a linear polynomial are two so the linear polynomial is either a binomial or a monomial.
- Polynomials having degree 2 are called quadratic polynomials. The maximum terms in a quadratic polynomial in one variable are three so the quadratic polynomial can be monomial, binomial, or trinomial.
- Polynomials having degree 3 are called cubic polynomials. The maximum terms in a cubic polynomial in one variable are four so the cubic polynomial can be monomial, binomial, or trinomial.
A polynomial in one variable x of degree n is expressed by the form –
P(x) = anxn + an-1xn-1 +…………+ a1x + a0
Where an ≠ 0, and an, an-1, a1, a0 = constants
Examples of Non-polynomials
- x + ⅟x
- √y + 5
- z-4 – z
Like Terms and Unlike Terms
Like Terms – In polynomials, if terms have the same algebraic factors, they are called like terms.
Examples –
- 4xy and 7xy
- 2x2z, x2z, and 9zx2
- 3abc, 8acb and 5cba
Unlike Terms – In polynomials, if terms have different algebraic factors, they are called, Unlike terms.
Examples –
- 7st and 6st2
- 3pqr, pqrs and 9p2
- 6sr, s3r, and rst
Operations on Polynomials
➤ Addition of polynomials
➤ Subtraction of polynomials
➤ Multiplication of polynomials
➤ Division of polynomials
Addition of Polynomials
When we add two or more polynomials then only like terms are added. it means terms with the same variables and the same powers are added. unlike terms will not be added, they will remain unchanged. In addition, the degree of the resultant polynomial remains the same.
Example – Add polynomials 3x2 + 4xy + 2y2 and 5y2 – xy + 7x2
Solution – 3x2 + 4xy + 2y2 + 5y2 – xy + 7x2
(3x2 + 7x2) + (4xy – xy) + (2y2 + 5y2)
10x2 + 3xy + 7y2 Ans.
Subtraction of Polynomials
Subtraction of the polynomials is the same as the addition of the polynomials. In this, like terms are subtracted and the unlike terms will be unchanged. In this also, the degree of the resultant polynomial will remain the same.
Example – Subtract the polynomial 3xy2 + 4xy – 6x2y + y3 from 8xy2 + 7xy + x2y.
Solution – 8xy2 + 7xy + x2y – (3xy2 + 4xy – 6x2y + y3)
8xy2 + 7xy + x2y – 3xy2 – 4xy + 6x2y – y3
(8xy2 – 3xy2) + (7xy – 4xy) + (x2y + 6x2y) – y3
5xy2 + 3xy + 7x2y – y3 Ans.
Multiplication of Polynomials
When two or more polynomials are multiplied then the result is always of a higher degree polynomial. But in two polynomials, if one or both of the polynomials are constant polynomials then the degree will remain the same. In the multiplication of polynomials, powers of the same variables are added by the laws of exponents.
Multiplying a Monomial by a Monomial
Multiplying two monomials
Examples – 1) 4x⨯6y = (4⨯6)⨯(x⨯y) = 24xy
2) 3a⨯(-2b) = {3⨯(-2)}⨯(a⨯b) = -6ab
3) 6p2⨯8p = (6⨯8)⨯(p2⨯p) = 48p3
4) x4yz2⨯2xy3z = (1⨯2)⨯(x4⨯x⨯y⨯y3⨯z2⨯z) = 2x5y4z3 Ans.
Multiplying three or more monomials
Examples – 1) 7t⨯2s⨯3r = (7⨯2⨯3)⨯(t⨯s⨯r) = 42tsr Ans.
2) 4pq⨯5p2q2⨯6p3q3
= (4⨯5⨯6)⨯(p⨯p2⨯p3⨯q⨯q2⨯q3)
= 120p6q6 Ans.
3) 2x2y⨯(-4y2z)⨯(-7z2x)⨯2x2yz
= [2x2y⨯(-4y2z)]⨯[(-7z2x)⨯2x2yz]
= (-8x2y3z)⨯(-14x3yz3)
= 112x5y4z4 Ans.
Multiplying a Monomial by a Polynomial
Multiplying a monomial by a binomial
Examples – 1) 2a⨯(3b+4)
Using Distributive law,
= 2a⨯3b + 2a⨯4
= 6ab + 8a Ans.
2) 7xy⨯(y2+5)
= 7xy⨯y2 + 7xy⨯5
= 7xy3 + 35xy Ans.
Multiplying a monomial by a trinomial
Examples – 1) 3v⨯(4v2+5v+7)
Using Distributive law,
= 3v⨯4v2 + 3v⨯5v + 3v⨯7
= 12v3 + 15v2 + 21v Ans.
2) x2⨯(9xz+6y2-xyz)
= x2⨯9xz + x2⨯6y2 – x2⨯xyz
= 9x3z + 6x2y2 – x3yz Ans.
Multiplying a Polynomial by a Polynomial
Multiplying a binomial by a binomial
Examples – 1) (2x+3y)⨯(3x+2y)
= 2x⨯(3x+2y) + 3y⨯(3x+2y)
= 2x⨯3x + 2x⨯2y + 3y⨯3x + 3y⨯2y
= 6x2 + 4xy + 9xy + 6y2
= 6x2 + 13xy + 6y2 Ans.
2) (p2-6qr)⨯(9q2+7r)
= p2⨯(9q2+7r) – 6qr⨯(9q2+7r)
= p2⨯9q2 + p2⨯7r – 6qr⨯9q2 – 6qr⨯7r
= 9p2q2 + 7p2r – 54q3r – 42qr2 Ans.
Multiplying a binomial by a trinomial
Examples – 1) (a+5)⨯(a2+2a-7)
= a⨯(a2+2a-7) + 5⨯(a2+2a-7)
= a⨯a2+a⨯2a-a⨯7 + 5⨯a2+5⨯2a-5⨯7
= a3+2a2-7a + 5a2+10a-35
= a3+7a2+3a-35 Ans.
2) (x2-3)⨯(xy+yz+zx)
= x2⨯(xy+yz+zx) – 3⨯(xy+yz+zx)
= x2⨯xy+x2⨯yz+x2⨯zx – 3⨯xy – 3⨯yz – 3⨯zx
= x3y + x2yz + x3z – 3xy – 3yz – 3zx Ans.
Division of Polynomials
In the division of polynomials, the result is a lesser degree polynomial and if one of the polynomials is a constant polynomial then the degree will remain the same.
Dividing a Monomial by a Monomial
For easy Division, we factorize both Dividend and Divisor in this type of Division.
Examples – 1) 6x4 ÷ 3x
= 2⨯3⨯x⨯x⨯x⨯x/3⨯x = 2⨯x⨯x⨯x = 2x3 Ans.
2) 72p2q3r ÷ (- 6p4q)
= 2⨯2⨯2⨯3⨯3⨯p⨯p⨯q⨯q⨯q⨯r/-2⨯3⨯p⨯p⨯p⨯p⨯q
= 2⨯2⨯3⨯q⨯q⨯r/-p⨯p = 12q2r/-p2 Ans.
Dividing a Polynomial by a Monomial
Examples – 1) (2xy + 6x) ÷ 2x
= (2xy + 6x)/2x = 2x(y + 3)/2x = (y+3) Ans.
2) (8y3 + 6y2 + 12y) ÷ 2y
= (8y3 + 6y2 + 12y)/2y = 2y(4y2 + 3y+ 6)/2y
= 4y2 + 3y+ 6 Ans.
This can be also solved as = 8y3/2y + 6y2/2y + 12y/2y = 4y2 + 3y+ 6
Dividing a Polynomial by a Polynomial
Examples – 1) (7a2 + 14a) ÷ (a + 2)
= (7a2 + 14a)/(a + 2) = 7a(a + 2)/(a + 2) = 7a Ans.
2) (x4 – 5x3 – 24x2) ÷ x(x – 8)
= (x4 – 5x3 – 24x2)/x(x – 8) = x2(x2 – 5x – 24)/x(x – 8)
= x(x2 – 8x + 3x – 24)/(x – 8) [factorization of (x2 – 5x – 24)]
= x{x(x – 8) + 3(x – 8)}/(x – 8)
= x(x – 8)(x + 3)/(x – 8) = x(x + 3) Ans.
If the above method does not help you to divide a polynomial by a polynomial, then there is also another method to divide which is called the Division Algorithm.
Solving Polynomials
To solve a polynomial, we put that polynomial equals zero (0) and find the value of the variable in it. Values of the variable are called zeroes or roots of the polynomial which depend on the degree of the polynomial. if the degree of the polynomial is 1 then there will be one zero or root and if the degree is 2 then there will be two zeroes or roots.
- Solving a linear polynomial
- Solving a quadratic polynomial
- Solving a cubic polynomial
Solving a Linear Polynomial
In the linear polynomial, the degree is always 1 so there will be one and only one zero. if the linear polynomial is p(x) then to find the zero of the polynomial p(x) we have to solve the equation p(x) = 0.
Example – 1) find the zero of the polynomial p(x) = 3x + 2.
Solution – let p(x) = 0
3x + 2 = 0
3x = – 2
x = -2/3
So, x = -2/3 is the zero of the polynomial p(x) = 3x + 2. Ans.
Example – 2) find the zero of the polynomial p(y) = 2y – 6.
Solution – let p(y) = 0
2y – 6 = 0
2y = 6
y = 6/2
y = 3
So, Zero of the polynomial p(y) = 2y – 6 is y = 3. Ans.
Note – Standard form of the linear polynomial is ax + b = 0 where a ≠ 0 so the zero will be x = -b/a. we can also find the zero by comparing it.
Solving a Quadratic Polynomial
In the quadratic polynomial, the degree is 2 so there will be two zeroes.
Example – 1) find the zeroes of the polynomial x2 – 3x.
Solution – let p(x) = x2 – 3x
Now P(x) = 0
x2 – 3x = 0
x(x – 3) = 0
x = 0 and x – 3 = 0
x = 0 and x = 3
Therefore, The two zeroes are x = 0 and x = 3. Ans.
Example – 2) find the zeroes of the polynomial 6x2 + 5x – 6.
Solution – let p(x) = 6x2 + 5x – 6
Now p(x) = 0
6x2 + 5x – 6 = 0
6x2 + 9x – 4x – 6 = 0 (By factorization method) [9−4 = 5 and 9⨯(-4) = -36]
3x(2x+3) – 2(2x+3) = 0
(2x + 3)(3x – 2) = 0
2x + 3 = 0 and 3x – 2 = 0
2x = -3 and 3x = 2
x = -3/2 and x = 2/3
These are the zeroes of the given polynomial. Ans.
Solving a Cubic Polynomial
In the cubic polynomial, the degree is 3 so there will be three zeroes. To solve the cubic polynomial first we have to arrange the polynomial in descending order then we solve it by taking common terms or by factorization.
Example – 1) find the zeroes of the polynomial x3 + 2x2 – x – 2.
Solution – let p(x) = x3 + 2x2 – x – 2
Now p(x) = 0
x3 + 2x2 – x – 2 = 0
x2(x + 2) – 1(x + 2) = 0
(x + 2)(x2 – 1) = 0
x + 2 = 0 and x2 – 1 = 0
x = -2 and x2 = 1
x = ±√1
x = ±1
So, the zeroes are x = -2, x = +1, and x = -1. Ans.
Note – We can check the answer by putting the value of each zero in the given polynomial because, at each value of zero, the value of the polynomial is 0.
Example – 2) find the zeroes of the polynomial x3 + 6x2 + 11x + 6.
Solution – let p(x) = x3 + 6x2 + 11x + 6
There is not any common term in it.
So, the factors of the constant term 6 = ±1, ±2, ±3 and ±6
Now at x = +1
p(1) = (1)3 + 6(1)2 + 11(1) + 6
p(1) = 1 + 6 + 11 + 6
p(1) = 24
∵ p(1) ≠ 0 so x = +1 is not the zero of this polynomial.
Here, all the terms in the polynomial are positive so we shall take only negative factors.
Now at x = – 1
p(-1) = (-1)3 + 6(-1)2 + 11(-1) + 6
p(-1) = -1 + 6 – 11 + 6
p(-1) = 0
∵ p(-1) = 0 so x = -1 is the zero of this polynomial.
Now at x = -2
p(-2) = (-2)3 + 6(-2)2 + 11(-2) + 6
p(-2) = – 8 + 6(4) – 22 + 6
p(-2) = – 8 + 24 – 22 + 6
p(-2) = 0
∵ p(-2) = 0 so x = -2 is the zero of this polynomial.
Now at x = -3
p(-3) = (-3)3 + 6(-3)2 + 11(-3) + 6
p(-3) = -27 + 6(9) – 33 + 6
p(-3) = -27 + 54 – 33 + 6
p(-3) = 0
∵ p(-3) = 0 so, x = -3 is the zero of this polynomial.
∵ The degree of the given polynomial is 3 so there will be only three zeroes.
So, the zeroes of the given polynomial are x = -1, x = -2, and x = -3. Ans.
Division Algorithm
If p(x) and g(x) are two such polynomials that the degree of p(x) is greater than g(x) and g(x) ≠ 0, and we divide p(x) by g(x) then we get two polynomials as quotient q(x) and remainder r(x) such that
p(x) = g(x).q(x) + r(x)
Where r(x) = 0 or the degree of the r(x) is smaller than g(x).
Example – Divide the polynomial p(x) = 2x4 – 3x3 + 3x + 1 by x + 1.
Solution –
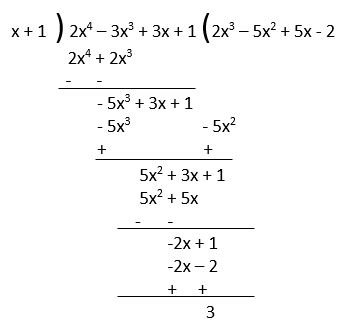
Quotient = 2x3 – 5x2 + 5x – 2 Remainder = 3
Steps –
- First of all, we arrange the dividend and divisor in descending order if they are not arranged.in this question, both are arranged in descending order.
- Then we divide the first term of the dividend by the first term of the divisor. We divide 2x4 by x and get 2x3. This is the first term of quotient.
- We multiply the divisor (x+1) by the first term of the quotient 2x3 and subtract the product 2x4 + 2x3 from the dividend. this gives the remainder -5x3 +3x + 1.
- This remainder -5x3 + 3x + 1 is our new dividend. we repeat step (2) to get the second term of the quotient as – 5x2.
- Similarly, like step (3) we multiply the second term of the quotient – 5x2 by the divisor (x+1) and subtract the product – 5x3 – 5x2 from the new dividend. We write the like term below the like term and if there is any unlike term then we write that term separately.
This process continues till the remainder is 0 or the degree of the new dividend is less than the degree of the divisor. At the last, the new dividend will be the remainder.
Here, zero of divisor x + 1 is x + 1 = 0 ⇒ x = -1
So, p(x) at x = -1, p(-1) = 2(-1)4 – 3(-1)3 + 3(-1) + 1
p(-1) = 2 – 3(-1) – 3 + 1
p(-1) = 2 + 3 – 3 + 1 = 3 (Remainder)
It means we can find the remainder r(x) of any division by putting the value of the zero of divisor g(x) in dividend p(x).
Remainder Theorem
Let p(x) be any polynomial of degree one or greater than one and let a be any real number. If p(x) is divided by the linear polynomial (x – a), then the remainder is p(a).
Example – find the remainder when x4 – 4x2 + x3 + 2x + 1 is divided by x – 1.
Solution – let p(x) = x4 – 4x2 + x3 + 2x + 1
Zero of x – 1 is x – 1 = 0 ⇒ x = 1
So, p(x) at x = 1, p(1) = (1)4 – 4(1)2 + (1)3 + 2(1) + 1
p(1) = 1 – 4 + 1 + 2 + 1 = 1
Therefore, Remainder is 1. Ans.
Factor Theorem
If polynomial p(x) is divided by polynomial g(x) with remainder r(x) = 0 then the polynomial g(x) will be one factor of polynomial p(x) or we can say if g(x) is one factor of p(x) then the remainder r(x) will be zero.
Example – examine whether x – 3 is a factor of polynomial x3 – 3x2 + 4x – 12.
Solution – let p(x) = x3 – 3x2 + 4x – 12
We know if (x – 3) is a factor of p(x) then the remainder will be 0.
the zero of x – 3 is x – 3 = 0 ⇒ x = 3
Now p(x) at x = 3, p(3) = (3)3 – 3(3)2 + 4(3) – 12
p(3) = 27 – 3(9) + 12 – 12
p(3) = 27 – 27 + 12 – 12 = 0
∵ The remainder is 0 so (x – 3) is the factor of polynomial p(x). Ans.
Note – Here, zero is x = 3 so the factor is x – 3. We can find the factor if we know the zero and we can find the zero if we know the factor of any polynomial.
Relationship Between Zeroes and Coefficients of a Quadratic Polynomial
We know the standard form of a quadratic polynomial is f(x) = ax2 + bx + c.
Let α and β be two zeroes of this polynomial. Then (x – α) and (x – β) will be factors of f(x).
So, for constant k we can write,
f(x) = k(x – α) (x – β)
ax2 + bx + c = k{x2 – (α + β)x + αβ}
ax2 + bx + c = kx2 – k(α + β)x + kαβ
by comparing, a = k, b= – k(α + β), c = kαβ
∵ b= – k(α + β) and c = kαβ
α + β = b/-k and αβ = c/k
∵ a = k
α + β = b/-a or -b/a and αβ = c/a
So, for quadratic polynomial f(x) = ax2 + bx + c
Sum of zeroes (α + β) = -b/a = -(coefficient of x)/(coefficient of x2)
Product of zeroes (αβ) = c/a = (constant term)/(coefficient of x2)
Some Examples
Example – 1) find the zeroes of the quadratic polynomial 3x2 + 5x – 2 and verify the relationship between the zeroes and the coefficients.
Solution – let f(x) = 3x2 + 5x – 2
Now f(x) = 0
3x2 + 5x – 2 = 0
3x2 + 6x – x – 2 = 0
3x(x + 2) – 1(x + 2) = 0
(x + 2)(3x – 1) = 0
x + 2 = 0 and 3x – 1 = 0
x = – 2 and x = ⅓
So, the zeroes of polynomial f(x) are x = – 2 and x = ⅓
Now, sum of the zeroes = – 2 + ⅓ = (-6 + 1)/3 = -5/3 = -(coefficient of x)/(coefficient of x2)
Product of zeroes = – 2⨯⅓ = -2/3 = (constant term)/(coefficient of x2)
So, the relationship between the zeroes and the coefficients of the quadratic polynomial is verified.
Example – 2) find a quadratic polynomial, whose sum and product of zeroes are -6 and 5 respectively.
Solution – let α and β be the zeroes of a quadratic polynomial.
For any constant k, the quadratic polynomial will be
k{x2 – (α + β)x + αβ}
In question, the sum of zeroes (α + β) = – 6
Product of zeroes (αβ) = 5
Putting the values,
k{x2 – (- 6)x + 5}
k{x2 + 6x + 5} [Where k = Constant]
So, the required quadratic polynomial is x2 + 6x + 5. Ans.
Example – 3) find all the zeroes of polynomial f(x) = x3 + 13x2 + 32x + 20, if it’s one zero is – 2.
Solution – Here, – 2 is zero so the factor will be (x + 2). It is one factor of f(x).
To find other zeroes we will divide polynomial f(x) by factor (x + 2).
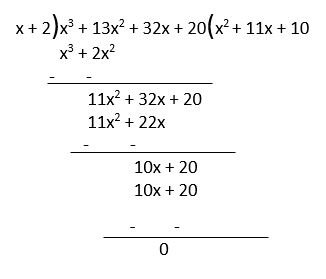
From the division algorithm, quotient x2 + 11x + 10 will be its factor because the remainder is 0.
Now Dividend = Divisor ⨯ Quotient + Remainder
x3 + 13x2 + 32x + 20 = (x + 2)⨯(x2 + 11x + 10) + 0
x3 + 13x2 + 32x + 20 = (x + 2)⨯{ x2 + 10x + x + 10}
x3 + 13x2 + 32x + 20 = (x + 2)⨯{ x(x + 10) + 1(x + 10)}
x3 + 13x2 + 32x + 20 = (x + 2)⨯(x + 10)(x + 1)
To find zeroes, f(x) = 0
(x + 2)(x + 10)(x + 1) = 0
x = -2, x = -10 and x = -1
So, all the zeroes of polynomial f(x) are -2, -10, and -1. Ans.


























































































































































I love it when folks get together and share views. Great blog, keep it up!
Thanks for sharing. I read many of your blog posts, cool, your blog is very good. https://accounts.binance.com/vi/register?ref=UM6SMJM3
whoah this blog is magnificent i love reading your articles.
Keep up the great work! You understand, many persons are looking
around for this information, you can aid them greatly.
Thank You.