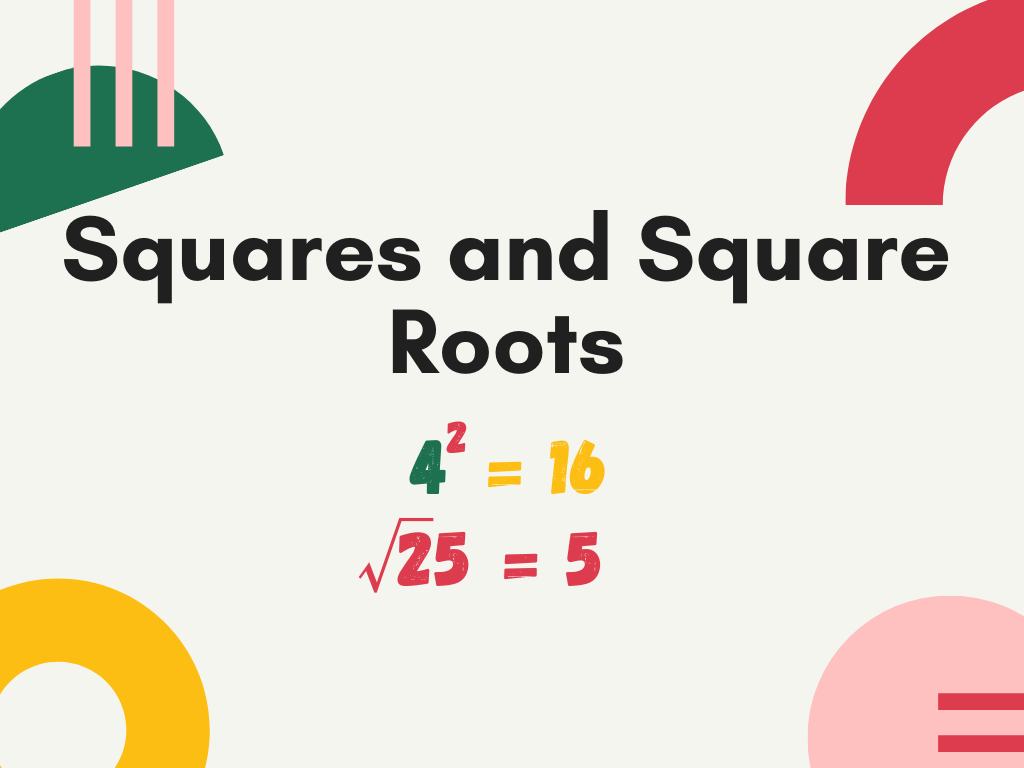Real Numbers Class 8th

Introduction

As the name suggests, these numbers are real for mathematical calculations. There are different types of real numbers. In class 8^th, we will get into the definition, types with examples, and properties of Real Numbers.

Definition

All rational numbers and irrational numbers are called Real Numbers. Real numbers are denoted by R.

Examples – 0, 2, −1, 3.6, 5/6, 8.567567……., π(3.1415……), etc.

Types of Real Numbers

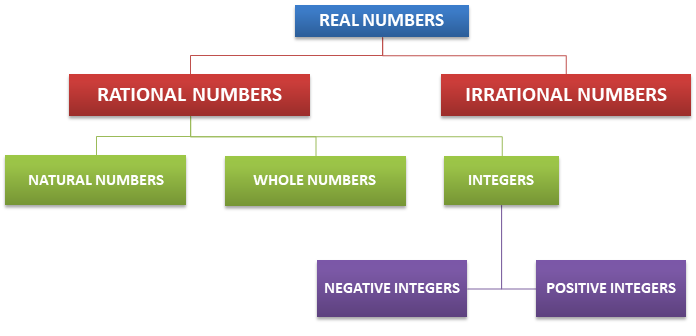
Rational Numbers – The numbers that can be written in the form of p/q, are called Rational Numbers. Where p and q are integers and q ≠ 0. Rational numbers are denoted by Q.

Examples – 1/2, 3/5, −7/2, 1/−3, etc.

Natural Numbers – All the counting numbers starting from 1 are called Natural Numbers. Natural numbers are denoted by N.

Examples – 1, 2, 3, 4, 5, 6………∞ (infinity).

Whole Numbers – All the natural numbers including 0 are called Whole Numbers. Whole numbers are denoted by W.

Examples – 0, 1, 2, 3, 4, 5, 6……….∞ (infinity).

Integers – All the positive and negative numbers including 0 are called Integers. Integers are denoted by Z.

Examples – −∞………..−4, −3, −2, −1, 0, 1, 2, 3, 4………..∞.

There are two types of Integers –

1. Positive integers – Positive numbers are called Positive Integers. They are denoted by Z⁺. Examples – 1, 2, 3, 4, 5……∞
2. Negative integers – Negative numbers are called Negative Integers. They are denoted by Z^–. Examples – −1, −2, −3, −4…….−∞

Note – Positive integers including 0 are called whole numbers.

Irrational Numbers – The numbers that cannot be written in the form of p/q, are called Irrational Numbers. Where p and q are integers and q ≠ 0. Irrational numbers are denoted by T. They can also be represented by R\Q, Where R shows the Real numbers and Q shows the Rational numbers. The meaning of R\Q is the group of numbers except Rational numbers in Real numbers which are Irrational numbers.

Examples– √2, √3, √5, √7, 1.2345728904……, π(3.1415926535897932…….), etc.

Properties of Real Numbers

There are four types of properties of real numbers –

1. Commutative Property
2. Associative Property
3. Distributive Property
4. Identity Property

(1) Commutative Property – For real numbers, the Commutative property is used only in addition and multiplication. If A and B are two real numbers then

For addition – A+B = B+A

Examples – 1) 2 + 3 = 3 + 2 = 5     Here, A = 2 & B = 3

2) −4 + 5 = 5 + (−4) = 1   Here, A = −4 & B = 5

For multiplication – A×B = B×A

Examples –1) 3×4 = 4×3 = 12    Here, A = 3 & B = 4

2) 1×(−6) = −6×1 = −6    Here, A = 1 & B = −6

Note – The Commutative property is not used in subtraction and division for real numbers.

(2) Associative Property – Associative property is also used in addition and multiplication only. If A, B, and C are three real numbers then

For addition – A + (B+C) = (A+B) + C

Examples – 1) 3 + (4+5) = (3+4) + 5 =12   Here, A = 3, B = 4 & C = 5

2) 3 + {4+(−5)} = (3+4) + (−5) = 2      Here, A = 3, B = 4 & C = −5

For multiplication – A×(B×C) = (A×B)×C

Examples – 1) −1×(−4×5) = {−1×(−4)}×5 = 20     Here, A = −1, B = −4 & C = 5

2) −2×(1×5) = (−2×1)×5 = −10      Here, A = −2, B = 1 & C = 5

Note – The associative property is not used in subtraction and division for real numbers.

(3) Distributive Property – If A, B & C are three real numbers then the distributive property is as follows –

A×(B+C) = A×B + A×C

Examples – 1) 5×(6+7) = 5×6 + 5×7    Here, A = 5, B = 6 & C = 7

5×(13) = 30+35

65 = 65

2) 2×(−3+7) = 2×(−3) + 2×7    Here, A = 2, B = −3 & C = 7

2×(4) = −6 + 14

8 = 8

(4) Identity Property – There are two types of identity property

1. Additive identity
2. Multiplicative identity

(1) Additive identity – When 0 is added to any real number then the result is always the same real number. 0 is the additive identity for real numbers. If A is a real number, then its additive identity will be

A+0 = 0+A = A

Examples – 1) 5+0 = 0+5 = 5   Here, A = 5

2) −9+0 = 0+(−9) = −9     Here, A = −9

(2) Multiplicative identity – When 1 is multiplied by any real number then the result is always the same real number. 1 is the multiplicative identity for real numbers. If A is a real number, then its multiplicative identity will be

A×1 = 1×A = A

Examples – 1) 7×1 = 1×7 = 7     Here, A= 7

2) −5×1 = 1×(−5) = −5    Here, A= −5

Real Numbers Class 8^th in Hindi

More About Real Numbers