Introduction
In the number system, we have already studied whole numbers, natural numbers, integers, fractions, decimal numbers, etc. All of these types of numbers have different properties. In class 8th, we shall study Rational numbers, their definition and properties, the representation of rational numbers on the number lines, etc.
Definition of Rational Number
A number that can be expressed in the form of p/q, is called a Rational Number. Where p and q are integers and q ≠ 0.
Examples – 1/3, ½, 3/5, -5/2, 7/-8, ¼, etc.
How to Represent Rational Numbers on the Number Line
In the previous class, we learned the representation of natural numbers, whole numbers, integers, fractions, and rational numbers on the number line. There is a method to represent a rational number on the number line. Let us recall the method again with the help of some examples.
Method –
Example 1) Represent rational number ¾ on the number line.
Solution – 1) First of all, we draw the number line with 0 and only positive numbers 1, 2, 3, 4, and 5…. because the given rational number is positive.

2) In the given rational number denominator is 4 so we divide each of the numbers on the number line by 4.

3) In the above number line, we can see the rational number ¾. We mark the rational number ¾ with the help of a circle and arrow.
4) This is the required method to represent a rational number on the number line.
Example 2) Represent rational number -6/5 on the number line.
Solution – 1) First, we draw the number line with 0 and only negative numbers -1, -2, -3, -4, -5…. because the given rational number is negative.

2) We can see the denominator of the given rational number is 5. So, we divide each of the numbers on the number line by 5.
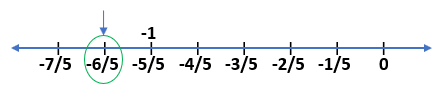
3) Our required rational number is -6/5 and we can see that on the above number line.
4) We mark the rational number -6/5 with the help of a circle and arrow.
5) Thus, we represent the rational number -6/5 on the number line.
Example 3) Represent the rational number 4/9 on the number line.
Solution – 1) First of all, we draw the number line with 0 and only positive numbers 1, 2, 3, 4, 5…. because the given rational number is positive.

2) In the given rational number denominator is 9 so we divide each of the numbers on the number line by 9.
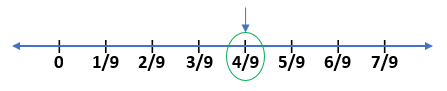
3) Our required rational number is 4/9 and we can see that on the above number line.
4) We mark the rational number 4/9 with the help of a circle and an arrow.
5) Thus, we represent the rational number 4/9 on the number line.