Surface Areas and Volumes Class 10th

Introduction

We are familiar with solid shapes or 3D (three-dimensional) shapes like cubes, cuboids, cylinders, cones, spheres, etc. We have studied these shapes and their properties in the previous classes. In class 9^th, we studied the basics of surface areas and volumes of solid shapes. We know all the formulae related to surface areas and volumes of solid shapes. In this class, we shall explore more and will find the surface area and volume of the combination of solids, conversion of a solid from one shape to another shape, frustum of a cone, etc. Before starting the main part of this chapter, we recall the solid shapes one by one and their formulae that we have already studied.

What are Surface Area and Volume?

The area of the total surface of the solid shapes is known as surface area. The measure of the space occupied by the solid shapes is called volume.

Cube

The cube is a solid shape that has 6 faces, 8 vertices, and 12 edges. All the faces and edges are of equal measurement. Each face of a cube is the shape of a square.

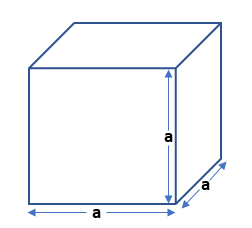
Surface Area and Volume of a Cube

The surface area of a cube = 6a²

The volume of a cube = a³

Where a = each edge of the cube.

Note – Sometimes the surface area of a cube is also named as Total surface area (TSA).

Lateral Surface Area of a Cube

Apart from the top and bottom surfaces of a cube, the rest of the surfaces are lateral surfaces. It means there will be only four surfaces in the lateral surface. The area of these four surfaces is called the lateral surface area of the cube.

Lateral Surface Area of a Cube = 4a²

The Diagonal of a Cube

The distance between opposite vertices in the cube is known as the Diagonal of a cube. This distance is the maximum distance inside the cube.

The diagonal of a cube = a√3

Note – The diagonal of the cube is measured in the distance unit.

Cuboid

The cuboid is a solid shape that has 6 faces, 8 vertices, and 12 edges. Opposite faces of the cuboid are of equal measurements. Each face of a cuboid is the shape of a rectangle.

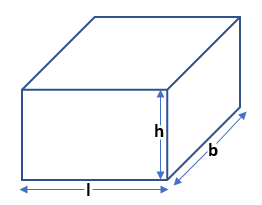
Surface Area and Volume of a Cuboid

Surface area of a cuboid = 2lb + 2bh + 2hl = 2(lb + bh + hl)

The volume of a cuboid = l×b×h

Where l, b, and h = three edges of the cuboid (length, breadth, and height).

Lateral Surface Area of a Cuboid

Apart from the top and bottom surfaces of a cuboid, the rest of the surfaces are lateral surfaces. It means there will be only four surfaces in the lateral surface. The area of these four surfaces is called the lateral surface area of the cuboid. In the bottom and top surfaces, length (l) and breadth (b) are the measurements of the edges so we will not use the term 2lb in the lateral surface area.

Lateral Surface Area of a Cuboid = 2lh + 2bh = 2(lh + bh)

The Diagonal of a Cuboid

The distance between opposite vertices in the cuboid is known as the Diagonal of a cuboid. This distance is the maximum distance inside the cuboid.

Diagonal of a cube = √(l² + b² + h²)

Note – The diagonal of the cuboid is measured in the distance unit.

Cylinder

The cylinder is also known as a right circular cylinder because it is made of many circular parts and these parts are kept vertically at the right angle.

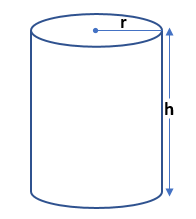
Surface Area and Volume of a Cylinder

Curved surface area (CSA) of a cylinder = 2πrh

Total surface area (TSA) of a cylinder = 2πrh + 2πr² = 2πr(h + r)

The volume of a cylinder = πr²h

Where, r = radius of the circular part

h = height of the cylinder

Note – In the place of the right circular cylinder, generally we use the word cylinder.

Cone

The cone is also known as the right circular cone because its base is a circular part and the line joining its vertex to the Centre of its base lies at the right angle.

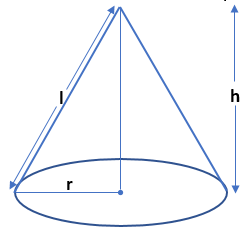
Surface Area and Volume of a Cone

Curved surface area (CSA) of a cone = πrl

Total surface area (TSA) of a cone = πrl + πr² = πr(l + r)

Volume of a cone = 1/3 (πr²h) = πr²h/3

Where, r = radius of the circular base

l = slant height of the cone

h = height of the cone

Slant Height of a Cone

When we draw the radius of the circular base of a cone and join the Centre of this circular base to the vertex of the cone then we get a right-angled triangle. The hypotenuse side of this right-angled triangle is called the slant height of the cone. We can find slant height by applying the Pythagoras theorem in the right-angled triangle.

The slant height of a cone (l) = √(h² + r²)

Sphere

A sphere is a 3D form of a circle. If we establish an axis through the center of a circle and rotate the circle with respect to that axis then we get a solid shape. That solid shape is called a sphere. A sphere is similar to a ball.

Surface Area and Volume of a Sphere

The surface area of a sphere = 4πr²

Volume of a sphere = 4/3 (πr³) = 4πr³/3

Where, r = radius of the sphere

Surface Area and Volume of a Hemisphere

If we divide a sphere into two equal parts then each part is half of the sphere. Each equal part is called a hemisphere.

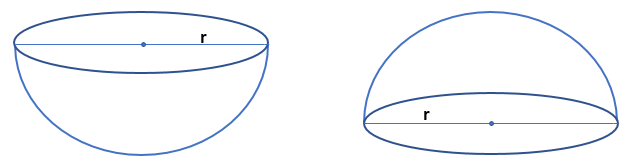
Curved surface area (CSA) of a hemisphere = half of the surface area of a sphere

CSA of a hemisphere = ½ (4πr²) = 2πr²

Total surface area (TSA) of a hemisphere = half of the surface area of a sphere + the area of a circle

TSA of a hemisphere = 2πr² + πr² = 3πr²

The volume of a hemisphere = half of the volume of a sphere

Volume of a hemisphere = ½ (4πr³/3) = 2/3 (πr³) = 2πr³/3

Where, r = radius of the hemisphere

Note – The surface area is measured in the square unit and volume is measured in the cubic unit.

Surface Area and Volume of Spherical Shell

Surface Area and Volume of a Combination of Solids

Conversion of a Solid from One Shape to Another Shape

Frustum of a Cone

Surface Areas and Volumes Class 10th in Hindi

More About Surface Areas and Volumes