Introduction
The Fundamental Theorem of Arithmetic is related to Number System. We have already studied prime numbers and composite numbers. The numbers which are divisible by 1 or the number itself are called Prime Numbers and the numbers which are divisible by other numbers also are called Composite Numbers. The factors of a prime number are 1 and the number itself (1×P). There is a relation between composite numbers and prime numbers that if we factorize a composite number till the last stage we shall get prime numbers as its factors.
Explanation
Let’s understand some examples with the help of the factoring process.
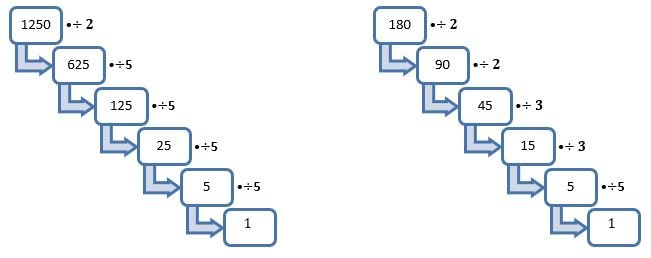
1250 = 2×5×5×5×5 and 180 = 2×2×3×3×5
Or we can write 1250 = 2×54 and 180 = 22×32×5
If we change the order of prime numbers then let’s see what happens.
Example – 765 = 3×3×5×17 or 765 = 32×5×17
if we factorize it in a different order then
765 = 5×3×3×17 or 765 = 5×32×17
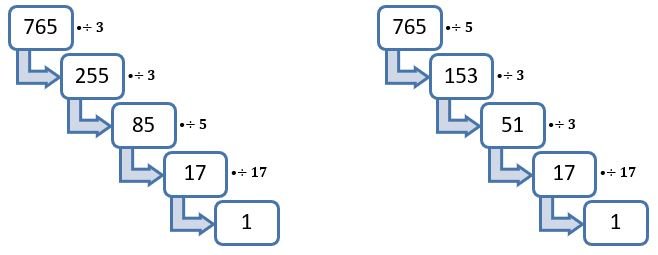
We saw that there is not any change in the factors, after factorizing with a different order. In both orders, the factors are remaining the same so we can easily factorize any composite number. It is recommended that the prime factors should be in ascending order to make the same factors in the exponent and in a unique way.
From the above examples, we can understand that any composite number can be written as the product of prime numbers. This is called The Fundamental Theorem of Arithmetic. The product of prime numbers for every composite number is unique except the order of prime numbers.
The Fundamental Theorem of Arithmetic (Statement)
Every Composite Number can be expressed or factorized as the product of prime numbers and the factorization is unique for every composite number except the order of prime numbers.
Some Examples of it –
Example 1) Express the numbers 3045 and 832 as their prime factorization.
Solution – Factor process for the numbers 3045 and 832
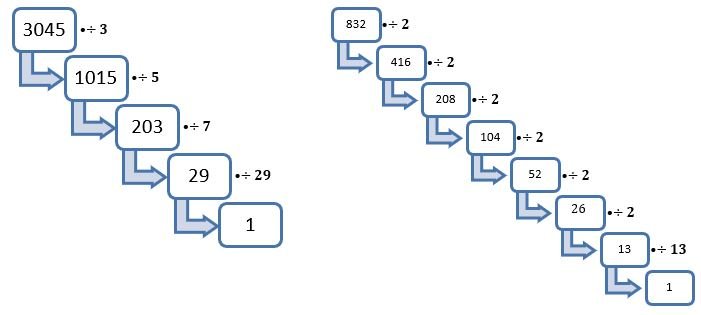
Prime Factors of 3045 = 3×5×7×29
Prime Factors of 832 = 2×2×2×2×2×2×13 Ans.
How to find LCM and HCF by Fundamental Theorem of Arithmetic
We have learned to find LCM and HCF by different methods. One of the methods is Prime Factorization which is also known as the fundamental theorem of arithmetic.
LCM (Least Common Multiple) = Product of the greatest power of each prime factor involved in the numbers.
HCF (Highest Common Factor) = Product of the smallest power of each common prime factor in the numbers.
Here, we shall use this method to find the HCF and LCM of two or more numbers with the help of some examples.
Example 2) Find the HCF and LCM of the numbers 15, 50, and 70 by the prime factorization method.
Solution – Prime factorization of 15, 50 and 70
15 = 3×5 15 = 3×5
50 = 2×5×5 = 2×52 50 = 2×5×5 = 2×52
70 = 2×5×7 70 = 2×5×7
HCF = 5 (Product of the smallest power of each common prime factor in the numbers)
LCM = 2×3×52×7 = 1050 (Product of the greatest power of each prime factor involved in the numbers)
Example 3) Find the HCF and LCM of the numbers 144 and 180 using the prime factorization method.
Solution – Prime factorization of 144 and 180
144 = 2×2×2×2×3×3 = 24×32 144 = 2×2×2×2×3×3 = 24×32
180 = 2×2×3×3×5 = 22×32×5 180 = 2×2×3×3×5 = 22×32×5
HCF = 22×32 = 4×9 = 36 LCM = 24×32×5 = 16×9×5 = 720 Ans.
In the above example,
If we multiply both the numbers 144×180 = 25920
And multiply HCF and LCM = 36×720 = 25920
We saw that the product of both numbers is equal to the product of HCF and LCM of both numbers.
This is the Fundamental Theorem of Arithmetic to find HCF and LCM. According to this theorem, for any two positive integers (A, B),
Product of A and B (A×B) = HCF (A,B) × LCM (A,B)
Or we can write, Product of two positive integers = HCF×LCM
We can use this formula to find the HCF or LCM of two positive integers if we have already found the LCM or HCF.
Example 4) Find the HCF of the numbers 125 and 200 by the prime factorization method. Find LCM also and verify whether the product of two numbers = HCF×LCM.
Solution – HCF by prime factorization,
125 = 5×5×5 and 200 = 2×2×2×5×5
125 = 53 and 200 = 23×52
HCF = 52
HCF = 25
So, LCM by formula, Product of two positive integers = HCF×LCM
125×200 = 25×LCM
(125×200)/25 = LCM
LCM = 5×200
LCM = 1000
Now, the product of two numbers = HCF×LCM
125×200 = 25×1000
25000 = 25000
LHS = RHS Proved.
Example 5) HCF and LCM of two numbers are 13 and 182 respectively if one number is 26 then find another number.
Solution – Let another number be X.
Here, HCF = 13, LCM = 182 and one number = 26
Since, the product of two numbers = HCF×LCM
X×26 = 13×182
X = (13×182)/26 = 182/2
X = 91
Thus, another number is 91. Ans.