Tangent and Secant of Circle Class 10th

Introduction

Definition of Tangent and Secant of Circle

Secant line – In a circle, if a line intersects the circle at two points, then that line is called the secant line of the circle.

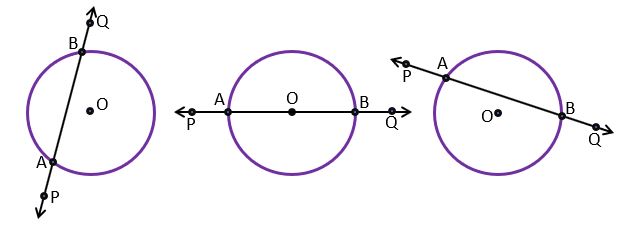
In the above figures, line PQ is a secant line that intersects the circles at points A and B which are called intersecting points. The Secant line always intersects the circle at two points. If we take intersecting points only then the secant line is the chord of the circle.

Tangent line – In a circle, if a line intersects the circle at one point, then the line is called the tangent line of the circle.

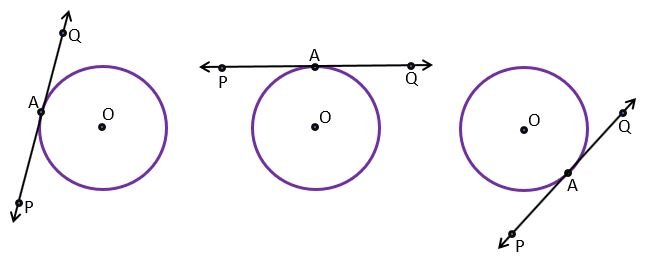
In the above figures, line PQ is the tangent line that intersects the circles at point A. tangent line always intersects the circle at one point. Tangent is the special case of a secant line in which both ends of its corresponding chord coincide with each other at a point.

The tangent line touches the circle at a point which is called the point of contact. This point is the common point of tangent lines and circles.

We cannot draw more than one tangent at the point of contact and if we try to draw then the other lines become secant lines.

Parallel Tangents in Circle

There are only two parallel tangent lines that can be drawn at a circle. This can be better understood by the figure below.

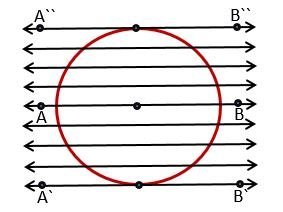
If we draw a secant line in the circle, let the secant line be AB and draw parallel secant lines above and below the secant line AB. We will see that the length of the corresponding chord of the secant line is decreasing and the intersecting points are coming closer to each other. At last, it will become zero on both sides of secant line AB. At this stage, the secant line is now A’B’ and A”B”. These are the tangents parallel to secant line AB and we can see that there are only two tangent lines in the circle that are parallel. The tangent line is perpendicular to the radius in a circle at the point of contact. This statement can be understood by the theorem.

Theorem 1) The tangent line drawn at any point of a circle is perpendicular to the radius at the point of contact.

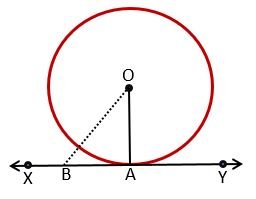
Given – OA is the radius of the circle and XY is the tangent at Point A.

Prove that – OA ⊥ XY

Construction – Took point B on tangent XY and joined OB.

Proof – There is a point B on the tangent XY. We can see that every point on the tangent will be outside the circle except point A which is situated on the point of contact.

For point B,

It is clear that OB > OA. [Because the distance of the point situated outside the circle is greater than the radius]

It means radius (OA) is the smallest distance from the point situated on tangent XY and it is also known that the perpendicular distance is the smallest distance from a straight line.

Therefore,         OA ⊥ XY Hence Proved.

Converse of Theorem

Theorem 2) If a line drawn from any point situated on the circle is perpendicular to the radius then it is tangent.

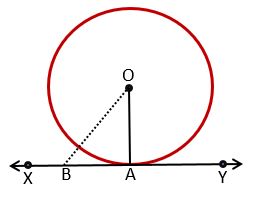
Given – OA is the radius of the circle and OA ⊥ XY.

Prove that – XY is a tangent on point A.

Construction – Took a point B on XY and joined OB.

Proof – ∵ OA ⊥ XY [given]

It means OA < OB [Because perpendicular distance is the smallest distance from the straight line]

So, all the points including point B, which are situated on line XY will be outside the Circle.

But point A will be on the circle because OA is the radius and line XY is drawn on it so, it is the common point of the circle and line XY.

And we know that the common point is the point of contact between the tangent and the circle.

Hence, XY is the tangent line.                  Hence Proved.

Number of Tangents Drawn from a Point on a Circle

How many tangents can be drawn from a point on a circle? this question can be solved when we know where the point is situated. We know that a circle divides the plane into three parts. (1) interior part (inside the circle) (2) on the circle (3) exterior part (outside the circle).

We shall find the tangents for all three conditions of three parts by figures.

(1) If the point is situated inside the circle – If the point is situated inside the circle then we can’t draw any tangent from that point. If we draw any line from that point, it will be a secant line and many secant lines can be drawn. Here is the figure for it.

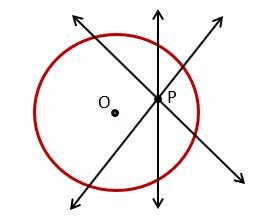
In the figure, P is the point situated inside the circle.

(2) If the point is situated on the circle – If the point is situated on the circle then we know that one and only one tangent line can be drawn from that point. Give a look at the figure.

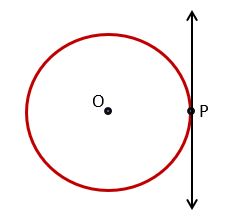
In the figure, P is the point situated on the circle. This point is called the Point of Contact.

(3) If the point is situated outside the circle – If the point is situated outside the circle then two tangent lines can be drawn from that point. The figure will show this.

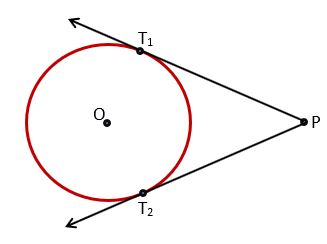
In the figure, P is the point situated outside the circle. The two tangents are PT₁ and PT₂. T₁ is the contact point of tangent PT₁ and T₂ is the contact point of tangent PT₂. The length from the tangent point of the circle to the exterior point P (P to T1) is called the length of the tangent. Here, PT1 and PT2 are the lengths of the tangents. There is a relationship between them. Both the lengths of tangents will be equal, but how? let’s see with the help of the theorem.

Theorem 3) The lengths of tangents drawn from an external point to a circle are equal.

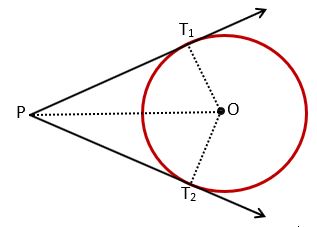
Given – PT₁ and PT₂ are two tangents drawn from external point P to the circle.

Prove that – PT₁ = PT₂

Construction – Joined points P, T₁ and T₂ to the Centre of the circle.

Proof – In △PT₁O and △PT₂O

∠PT₁O = ∠PT₂O = 90° [tangent is perpendicular to radius]

OP = OP [common side]

OT₁ = OT₂ [radii of the same circle]

By RHS criterion, △PT₁O ≅ △PT₂O        

So, by CPCT,          PT₁ = PT₂ Hence Proved.

Note – 1) In the above theorem, △PT₁O ≅ △PT₂O. so, by CPCT, ∠OPT₁ = ∠OPT₂.

It means OP is the angle bisector of ∠T₁PT₂ so, the Centre of the circle lies on the angle bisector of two tangents.

2) The above theorem can be proved by the Pythagoras theorem also.

PT₁² = OP² – OT₁²       and       PT₂² = OP² – OT₂²

∵ OT₁ = OT₂ [radii of the same circle]

Therefore,  PT₁² = OP² – OT₁² = PT₂² 

PT₁ = PT₂

Example

Example – If the distance of an external point from the Centre of the circle is 10 cm and the radius of the circle is 6 cm. then find the length of the tangent.

Solution –

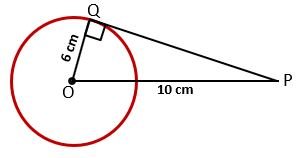
We know that the tangent is perpendicular to the radius of the circle.

In the figure, we can see that △PQO is a right-angled triangle.

So, by Pythagoras theorem,

PQ² = OP² – OQ²

PQ² = (10)² – (6)²

PQ² = 100 – 36 = 64

PQ = √64

PQ = 8 cm

So, the length of the tangent is 8 cm.            Ans.

Tangent and Secant of Circle Class 10^th in Hindi

More About Tangent and Secant of Circle