Fractions Class 7th

Definition

Before Studying Fractions in Class 7^th, we have already studied that fractions are the number that represents part of a group or of a region. Or we can say that fractions represent the part of a whole which may be a single object or group of objects. In the fraction, there are Numerator and Denominator. The Numerator represents a whole whereas The Denominator represents a part of a whole. Examples – ½, ⅔, 4/3, ⅘, ¼, ⅞, etc.

Types of Fractions

(1) Proper Fraction – The fraction in which the numerator is less than the denominator is called a Proper Fraction.

Example – ⅓, ¾, 5/9, 2/7, etc.

(2) Improper Fraction – The fraction in which the numerator is greater than the denominator is called an Improper Fraction.

Example – 3/2, 4/2, 8/3, 7/4, 9/8, etc.

(3) Mixed Fraction – The combination of a whole number and a proper fraction is known as a Mixed Fraction.

Example – 1¾, 4½, 7⅝, 3⅙, 8⅔, etc.

Note – The improper fraction can be written as a mixed fraction and the mixed fraction can be written as an improper fraction. Let’s understand with an example.

7/4 = improper fraction

On dividing 7 by 4.

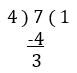
We can write 1¾ = mixed fraction

Now, 1¾ = (1×4 + 3) / 4

= (4 + 3) / 4

= 7/4 = improper fraction

Equivalent Fractions

An Equivalent fraction of any fraction represents the same part of a whole. There can be many equivalent fractions of a fraction.

Example – three equivalent fractions of ⅔

2×2 / 3×2 = 4/6

2×3 / 3×3 = 6/9

2×4 / 3×4 = 8/12

Note – To write equivalent fractions, we just multiply the same number to the numerator and the denominator of the fraction.

Comparison, Addition, and Subtraction of Fractions

In the comparison of two fractions, we convert them into like fractions by taking the LCM of their denominators.

Example – Which fraction is greater in 5/7 and ⅔?

Solution – Here, the denominators are 7 and 3.

LCM of 7 and 3 = 21

Now, we have to make the denominators of both fractions equal to 21.

So, we multiply 5/7 by 3 and multiply ⅔ by 7.

5×3 / 7×3 = 15/21      and       2×7 / 3×7 = 14/21

15/21 and 14/21 are like fractions.

Since numerator 15 > 14.

So, 15/21 > 14/21

Therefore, 5/7 > ⅔         Ans.

In the Addition, we add two or more than two fractions with the help of LCM when denominators are not the same. If denominators are the same, we simply add numerators of both fractions.

Example – Add 1) ¾ and 7/16    2) 8/9 and 2/9

Solution – 1) ¾ + 7/16

LCM of denominators 4 and 16 = 16

(3×4 + 7×1) / 16

(12 + 7) / 16

19/16            Ans.

2) 8/9 + 2/9

Here denominators are the same.

(8 + 2) / 9

10/9         Ans.

The Subtraction of two fractions is the same as the Addition. We subtract a fraction from another fraction with the help of LCM when denominators are not the same. If denominators are the same, we simply subtract numerators.

Example – Subtract 1) 1/6 from 6/7    2) 3/5 from 9/5

Solution – 1) 6/7 – 1/6

LCM of denominators 7 and 6 = 42

(6×6 + 1×7) / 42

(36 + 7) / 42

43/42            Ans.

2) 9/5 – 3/5

Here denominators are the same.

(9 – 3) / 5

6/5            Ans.

Multiplication of Fractions

We have multiplied whole numbers, natural numbers, integers, etc. The multiplication of these types of numbers is easy because of simple numbers. The multiplication of fractions is different from these numbers. Let’s see how to do it.

Multiplication of a Fraction by a Whole Number

In the multiplication of a fraction and a whole number, we multiply the whole number to the numerator of the fraction and the denominator remains unchanged. This multiplication is used directly for proper and improper fractions but for mixed fractions, first, we convert mixed fractions into improper fractions and then multiply.

Example – 1) multiply 5 and ¼.

Solution – 5× ¼ = 5×1 / 4 = 5/4            Ans.

Example – 2) multiply 3 and 8/7.

Solution – 3×8 / 7 = 24/7           Ans.

Example – 3) multiply 6 and 9¾.

Solution – 6×9¾ = 6×39/4 = 234/4 = 117/2           Ans.

Example – 4) find 4/5 of 9.

Solution – (4/5) ×9 = 4×9/5 = 36/5         Ans.

Note – In fractions, the operator ‘of ’ also represents the multiplication so we use the sign of multiply in place of the operator ‘of ’.

Multiplication of a Fraction by a Fraction

In the multiplication of a fraction by a fraction, we simply multiply the numerator of one fraction to the numerator of another fraction and the denominator of the same fraction to the denominator of another fraction. For proper and improper fractions, we use it directly but for mixed fractions, first, we convert mixed fractions into improper fractions and then multiply.

Example – 1) multiply 4/7 and 9/2.

Solution – (4/7) × (9/2) = (4×9) / (7×2) = 36/14 = 18/7          Ans.

Example – 2) multiply 2¼ and 5½.

Solution – 2¼×5½ = (9/4) × (11/2) = (9×11) / (4×2) = 99/8         Ans.

We can also write the product of two fractions = product of numerators/product of denominators

Note – 1) When we multiply two proper fractions, then the product is less than both fractions.

2) When we multiply two improper fractions or two mixed fractions, then the product is greater than both fractions.

3) When we multiply a proper fraction and an improper fraction, then the product is greater than the proper fraction and less than the improper fraction.

Division of Fractions

In the division of a whole number by another whole number, we use the division process and table of the divisor. The Division of fractions is something different because we can’t use the division process and table of the divisor in it. How can we divide a whole number by a fraction and a fraction by another fraction? Let’s see.

Division of a Whole Number by a Fraction

In the division of a whole number and a fraction, we convert the division sign into multiplication and write the reciprocal of the fraction and then multiply it.

Example – 1) Divide 6 by 5/2.

Solution – 6 ÷ 5/2 = 6×2 / 5 = 12/5        Ans.

Example – 2) Divide 3 by 1¼.

Solution – 3 ÷ 1¼ = 3 ÷ 5/4 = 3×4 / 5 = 12/5        Ans.

Note – 1) In the above example, the reciprocal of 5/2 is 2/5. To write the reciprocal of any fraction, we interchange the numerator and denominator.

2) When we divide a whole number by a mixed fraction, first we convert the mixed fraction into an improper fraction and then solve. 

Division of a Fraction by a Whole Number

In this division, we also convert the division sign into multiplication and write the reciprocal of the whole number, and then multiply. In the case of a mixed fraction, first, we convert the mixed fraction into an improper fraction and then solve it.

Example – 1) Divide 7/8 by 3.

Solution – 7/8 ÷ 3 = (7/8) × 1/3 = 7/24         Ans.

Example – 2) Divide 3¾ by 2.

Solution – 3¾ ÷ 2 = (15/4) × (1/2) = (15×1) / (4×2) = 15/8         Ans.

We know that every whole number has its denominator as 1 so, the reciprocal of 3/1 = 1/3.

Division of a Fraction by Another Fraction

Same as the above, we use the reciprocal of the divisor fraction and convert the division sign into multiplication. In the case of a mixed fraction, first, we convert the mixed fraction into an improper fraction and then solve it.

Example – 1) Divide 2/3 by 5/7.

Solution – 2/3 ÷ 5/7 = (2/3) × (7/5) = (2×7) / (3×5) = 14/15            Ans.

Example – 2) Divide 1½ by 4¼.

Solution – 1½ ÷ 4¼ = (3/2) ÷ (17/4) = (3/2) × (4/17) = (3×4) / (2×17) = 12/34           Ans.

Fractions Class 7^th in Hindi

More About Fractions