NCERT Maths Class 10th Solution

In this section, we shall study the NCERT Maths Class 10^th solution in English. In Maths class 10^th, there are 15 chapters. The solution is given chapter-wise in PDF format. In each PDF, every question of each exercise is solved in detail.

Chapter 1^st Real Numbers

NCERT maths class 10^th solution of chapter 1^st is given here. In Chapter 1^st Real Numbers, in exercise 1.1, questions based on Euclid’s division lemma, and Euclid’s division algorithm are solved with the help of an easy explanation. In exercise 1.2, questions based on the fundamental theorem of arithmetic, LCM, and HCF are solved. In exercise 1.3, there are 3 questions that are based on the irrationality theorem. We use the technique called ‘proof by contradiction’ to solve these questions. In exercise 1.4, there are 3 questions based on rational numbers and their decimal expansions, and their theorems. All the questions are solved in detail.

Chapter 1^st Real Numbers

Solution

Exercise 1.1

Q (1) Use Euclid’s division algorithm to find the HCF of:

(i) 135 and 225     (ii) 196 and 38220     (iii) 867 and 255

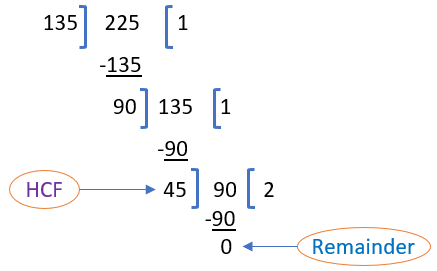
Solution – (i) 135 and 225

Using Euclid’s division algorithm        

Step 1 – Here, two positive integers are 135 and 225 and 225 > 135 so, by Euclid’s Division lemma.

225 = 135×1 + 90

Step 2 – Since the Remainder is not zero 90 ≠ 0 so, we shall apply Euclid’s Division Lemma to Divisor 135 and Remainder 90.

135 = 90×1 + 45

Step 3 – Again, the Remainder is not zero 45 ≠ 0 so, we shall apply Euclid’s Division Lemma to Divisor 90 and Remainder 45.

90 = 45×2 + 0

Since the remainder is zero in step 3 and the divisor in this step is 45.

Therefore, the required HCF of 135 and 225 is 45.                Ans.

We can also understand it by division process.

Continue in the PDF below.

NCERT Maths Class 10th Solution in Hindi