Definition
A Closed figure made of three line segments is called a Triangle. It has three sides, three angles, and three vertices. Here, Triangle ABC and its Properties are shown below.

Three sides – AB, BC, CA
Three angles – ∠A, ∠B, ∠C
Three vertices – A, B, C
Classification of Triangles –
➤ Based on Sides
❶ Scalene Triangle – The triangle in which all three sides are of different lengths, is called a Scalene Triangle. Because of all the different sides, all three angles are also of different measure in the scalene triangle.
❷ Isosceles Triangle – The triangle in which any two sides are of equal length, is called an Isosceles Triangle. Because of two equal sides, angles opposite to equal sides are also of equal measure in the isosceles triangle.

❸ Equilateral Triangle – The triangle in which all three sides are of equal length, is called an Equilateral Triangle. Because of all the equal sides, all three angles are also of equal measure (Each 60°) in the equilateral triangle.

➤ Based on Angles
❶ Acute Angled Triangle – The triangle in which all three angles are acute angles (Each angle is less than 90°), is called the Acute Angled Triangle.

❷ Obtuse Angled Triangle – The triangle in which any one angle is greater than 90°, is called the Obtuse Angled Triangle.
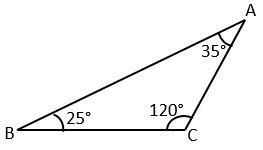
Here, ∠C = 120° (Obtuse angle)
❸ Right Angled Triangle – The triangle in which any one angle is equal to 90°, is called the Right-Angled Triangle.
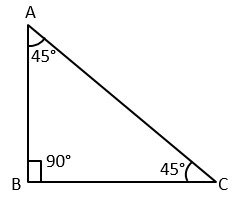
Here, ∠B = 90° (Right angle)
The Median of a Triangle
A line segment that connects a vertex of a triangle to the mid-point of its opposite side, is called the Median of a triangle.
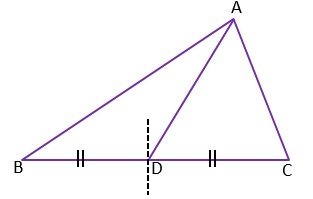
In the above figure, AD – median
BD = DC (∵ D is the midpoint of BC)
The Altitude of a Triangle
A line segment drawn from a vertex of a triangle to its opposite side at the angle of 90°(right angle), is called the Altitude of a triangle.

In the above figure, PS – Altitude
PS ⊥ QR
QS ≠ SR (∵ S is not the mid-point of QR)
Q 1) How many altitudes can be drawn in a triangle?
Ans. – 3
Q 2) How many Medians can be drawn in a triangle?
Ans. – 3
Exterior Angle of a Triangle and its Properties
Exterior Angle of a Triangle – In a triangle, if a side is extended in one direction from its vertex then the angle made in the external part of that vertex is called an Exterior angle of the triangle.

Theorem Based on it
Statement – Exterior angle of a triangle is equal to the sum of its interior opposite angles.
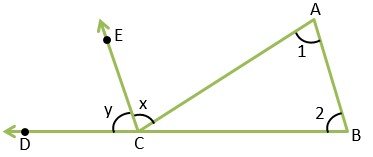
Given – In △ABC, exterior angle – ∠ACD, Interior opposite angles – ∠1 and ∠2
To prove – ∠ACD = ∠1 + ∠2
Construction – Drawn CE ∥ AB
So, let ∠ACE = ∠x and ∠ECD = ∠y
Proof – ∵ CE ∥ AB
∴ ∠1 = ∠x (Interior alternate angles are equal)……………..(1)
And ∠2 = ∠y (Corresponding angles are equal)……………….(2)
By adding equations (1) and (2)
∠1 + ∠2 = ∠x + ∠y
∠1 + ∠2 = ∠ACD
The above equation shows the exterior angle property of the triangle. Hence proved.
Example 1) Find the value of X?
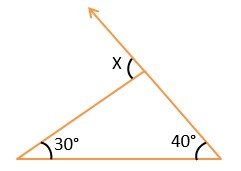
Solution – By exterior angle property,
X = 30° + 40°
X = 70° Ans.
Example 2) Find the value of X?
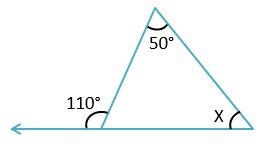
Solution – By exterior angle property
50° + X = 110°
X = 110° – 50°
X = 60° Ans.
Interior Angle Sum Property of a Triangle
Statement – The sum of the three angles of a triangle is 180°.
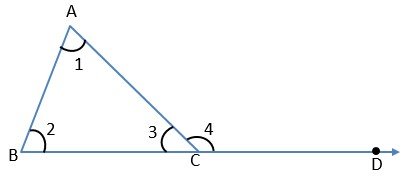
Given – ∠1, ∠2, and ∠3 are angles of ΔABC. Side BC is extended to D and ∠4 is the exterior angle.
To prove – ∠1 + ∠2 + ∠3 = 180°
Proof – By Exterior angle property of a triangle,
∠1 + ∠2 = ∠4 ……………..(1)
Adding ∠3 to both side ∠1 + ∠2 + ∠3 = ∠4 + ∠3 …………….(2)
But By Linear pair of Angle, ∠3 + ∠4 = 180° …………….(3)
So, by equations (2) and (3)
∠1 + ∠2 + ∠3 = 180°
This is the interior angle sum property of a triangle. Hence proved.
Example 1) Find the value of X?

Solution – By interior angle sum property of a triangle,
X + 50° + 60° = 180°
X + 110° = 180°
X = 180° – 110°
X = 70° Ans.
Example 2) Find the value of X?
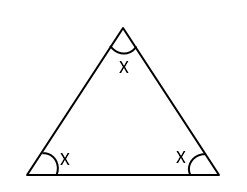
Solution – By interior angle sum property of a triangle,
X + X + X = 180°
3X = 180°
X = 180°/3
X = 60° Ans.
The Above triangle is an Equilateral triangle.
Other Properties of the Triangle
➞ The Sum of any two sides of a triangle is always greater than the third side.
➞ The Difference of any two sides of a triangle is always less than the third side.
➞ The Sum of all exterior angles of a triangle is 360°.
The Perimeter of a Triangle –
The Perimeter of a triangle is the sum of all three sides of a triangle. The Perimeter of a triangle is calculated in the length unit.
Perimeter = Sum of all the three sides
For △ABC, the sides will be AB, BC, and CA then
Perimeter = AB + BC + CA
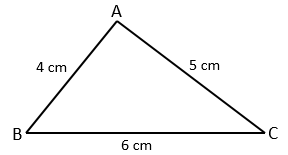
Example – Find the perimeter of the given triangle.

Solution – Perimeter = AB + BC + CA
Perimeter = 4 cm + 6 cm + 5 cm
Perimeter = 15 cm Ans.
Area of a Triangle –
The area enclosed by the three sides of the triangle is the area of the triangle. The area of a triangle is calculated in a square unit.
There are two methods to calculate the area of a triangle –
➊ When the Base and height are given
➋ When all three sides are given
➊ When the Base and height are given – If the base and height of a triangle are given then
The area of the triangle = ½⨯Base⨯Height
= ½⨯B⨯H Square Unit
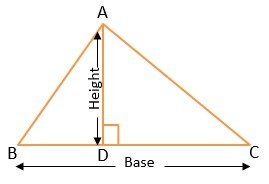
Example – Find the area of the triangle whose base is 8 cm and height is 5 cm.
Solution – Here B = 8 cm and H = 5 cm
Area of the Triangle = ½⨯B⨯H
= ½⨯8cm⨯5cm
= 4⨯5
= 20 Square cm or cm2 Ans.
➋ When all three sides are given – When all three sides are given we use Heron’s formula to find the area of the triangle.
Area of the triangle by Heron’s formula = √s(s-a)(s-b)(s-c)
Where s = Semi-perimeter of the triangle
s = a+b+c/2
a, b, c = Sides of a triangle
Example – Find the area of the triangle whose sides are 3 cm, 5 cm, and 6 cm.
Solution – Here a = 3 cm, b = 5 cm and c = 6 cm
So, Semi-perimeter (s) = a+b+c/2 = 3+5+6/2 = 14/2 = 7 cm
Now Area of triangle = √s(s-a)(s-b)(s-c)
= √7(7-3)(7-5)(7-6)
= √7(4)(2)(1)
= √7⨯2⨯2⨯2
= 2√14 cm2 Ans.