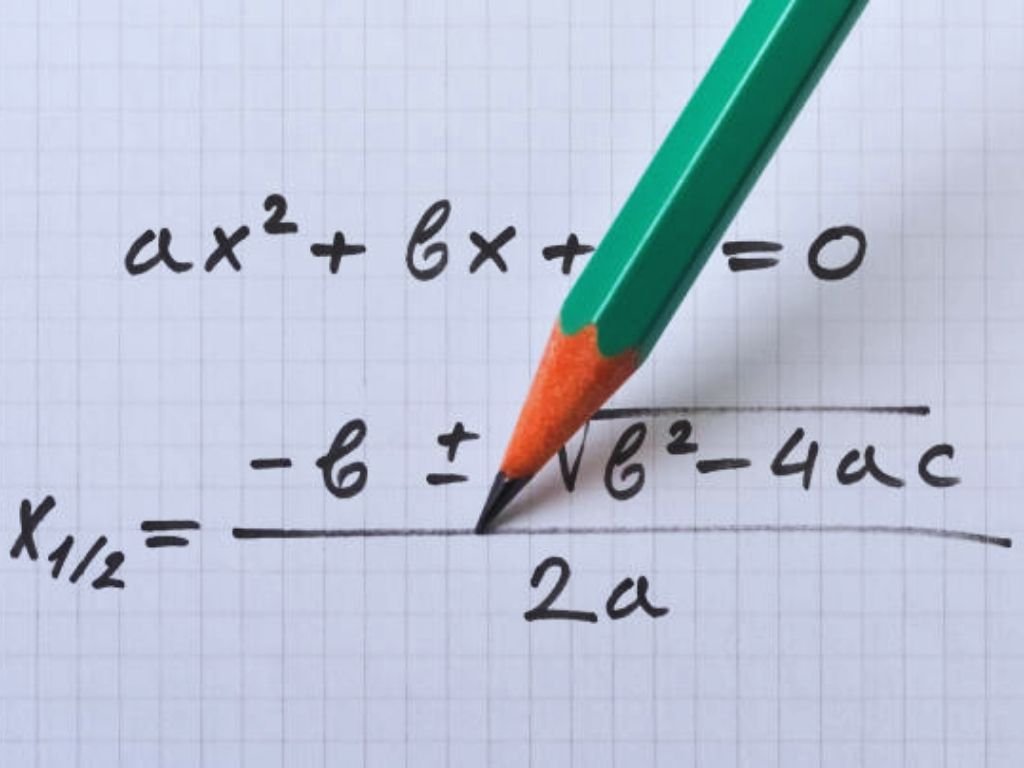Sum of First n Terms of an Arithmetic Progression Class 10th

Introduction

We know that there are n terms in an Arithmetic Progression (AP) and if we want the sum of the first n terms of an Arithmetic Progression then what should we do, we shall add all the terms of the AP but that will take more time to solve. Sometimes this method will not give the answer, to add first n terms of an Arithmetic Progression there is a formula for an easy solution.

Before the formula, let’s take an example to understand it clearly.

Explanation

I gave some money to my friend to help him and he gave me the money in instalments like in the first month he gave me 1000 rupees, in the second month he gave me 2000 rupees and so on. He gave all the money in 15 months in this order. Now I want to calculate that after 15 months how much money did I get? So I shall have to add all the instalments but that will take too much time. How can I add all the instalments in a shorter way? There is a formula to add easily. How can we get the formula, let’s see?

If I write all the instalments to get a sum and the sum is denoted by S

S = 1000 + 2000 + 3000 +…………………+ 13000 + 14000 + 15000

Now let’s rewrite all the terms in reverse order

S = 15000 + 14000 + 13000 +…………….…+ 3000 + 2000 + 1000

Now adding both the series

S + S = (1000 + 15000) + (2000 + 14000) + (3000 + 13000) + …….+ (13000 + 3000) + (14000 + 2000) + (15000 + 1000)

2S = 16000 + 16000 + 16000 +……….+ 16000 + 16000 + 16000 (15 times)

Therefore, 2S = 16000⨯15

S = 16000⨯15/2 = 8000⨯15

S = 120000

it means I shall get 1,20,000 rupees after 15 months.

Similarly, same as the above method, we can generate the formula to find the sum of the first n terms of an Arithmetic Progression.

Derivation of the Formula

We write the AP with first term a and common difference d for n terms as follows

a, a + d, a + 2d +………..+ a + (n – 1)d 

The sum of the first n terms of the Arithmetic Progression is denoted by S_n, so we can write

S_n = a + (a + d) + (a + 2d) + ………..+ [a + (n – 2)d] + [a + (n – 1)d] ………………(1)

Let’s rewrite all the terms in reverse order

S_n = [a + (n – 1)d] + [a + (n – 2)d] +……….+ (a + 2d) + (a + d) + a …………………(2)

Now, adding both equations (1) and (2)

S_n + S_n = [a + a + (n – 1)d] + [(a + d) + a + (n – 2)d] +…..+ [a + (n – 2)d + (a + d)] + [a + (n – 1)d + a]

2S_n = [2a + (n – 1)d] + [a + d + a + nd – 2d] +…..+ [a + nd – 2d + a + d] + [2a + (n – 1)d]

2S_n = [2a + (n – 1)d] + [2a + nd – d] +……………..+ [2a + nd – d] + [2a + (n – 1)d]

2S_n = [2a + (n – 1)d] + [2a + (n – 1)d] +……………..+ [2a + (n – 1)d] + [2a + (n – 1)d] {for n times}

2S_n =  [2a + (n – 1)d]⨯n

S_n = [2a + (n – 1)d]⨯n/2

S_n = n/2[2a + (n – 1)d]

So, the sum of the first n terms of an Arithmetic Progression        S_n = n/2[2a + (n – 1)d] 

Where S_n = Sum of first n terms of an AP

n = Number of terms

a = First term

d = Common difference

This can also be written as S_n = n/2[a + a + (n – 1)d]

S_n = n/2[a + a_n]                [∵ n^th term a_n = a + (n – 1)d]

If there are only n terms in AP then a_n = l (last term)

Therefore,       S_n = n/2[a + l]

If the first term (a) and the last term ( l ) are given then the above formula is useful.

If we want to solve the above-solved example with the help of a formula then first term (a) = 1000, last term ( l ) = 15000, number of terms (n) = 15

So, the sum will be S₁₅ = 15/2[1000 + 15000]

S₁₅ = 15/2[16000]

S₁₅ = 15⨯8000

S₁₅ = 120000

We can see that we have solved it very conveniently with the help of a formula.

Note – The n^th term of an AP is equal to the difference of the sum of the first n terms and the sum of the first (n – 1) terms.

i.e.        a_n = S_n – S_{n – 1}        

Let’s prove it.

RHS = S_n – S_{n – 1}

= n/2[2a + (n – 1)d] – (n-1)/2[2a + {(n – 1) – 1}d]

= n/2[2a + nd – d] – (n-1)/2[2a + (n – 2)d]

= 1/2[2an + n²d – nd] – 1/2[2a(n – 1) + nd(n – 1) – 2d(n – 1)]

= 1/2[2an + n²d – nd – 2a(n – 1) – nd(n – 1) + 2d(n – 1)]

= 1/2[2an + n²d – nd – 2an + 2a – n²d + nd + 2dn – 2d]

= 1/2[2a + 2dn – 2d]

= 2/2[a + dn – d]

= a + (n – 1)d

= a_n = LHS                    Hence Proved.

Some Examples –

Example 1) Find the sum of the first 16 terms of the AP: 1, 10, 19, 28………….

Solution – Here first term (a) = 1, common difference (d) = 10 – 1 = 9

The number of terms (n) = 16,   S16 =?

By the formula of sum of first n terms, S_n = n/2[2a + (n – 1)d]

Putting the values       S₁₆ = 16/2[2⨯1 + (16 – 1)9]

S₁₆ = 8[2 + 15⨯9]

S₁₆ = 8[2 + 135]

S₁₆ = 8[137]

S₁₆ = 1096

So, the sum of the first 16 terms is 1096.               Ans.

Example 2) Find the sum of the series: 10 + 7 + 4 + 1 +………..+ (-80).

Solution – Here, the common difference (d) = 7 – 10 = -3

4 – 7 = -3

1 – 4 = -3

The common difference is the same so it is an AP.

First term (a) = 10, last term a_n = l = -80, number of terms (n) = ?

The sum of n terms (S_n) =?

So, first, we shall find the number of terms (n)

By the n^th term formula,    a_n = a + (n – 1)d

-80 = 10 + (n – 1)(-3)

-80 – 10 = -3n + 3

-90 = -3n + 3

3n = 90 + 3

n = 93/3 ⇒ n = 31

It means there are 31 terms in the given series.

So, the sum of the first 31 terms of the AP by the formula,   S_n = n/2[a + l ]

S₃₁ = 31/2[10 + (-80)]

S₃₁ = 31/2[10 – 80]

S₃₁ = 31/2[-70] = 31⨯(-35)

S₃₁ = -1085

Therefore, the sum of the first 31 terms is -1085.              Ans.

Example 3) How many terms of the AP: 19, 21, 23, 25,……….must be taken so that their sum is 115?

Solution – First term (a) = 19, common difference (d) = 21 – 19 = 2,   S_n = 115

The number of terms (n) =?

Since,   S_n = n/2[2a + (n – 1)d]

115 = n/2[2⨯19 + (n – 1)2]

115⨯2 = n[38 + 2n – 2]

230 = 38n + 2n² – 2n

2n² + 36n – 230 = 0

2[n² + 18n – 115] = 0

n² + 18n – 115 = 0

By factorization method,       n² + 23n – 5n – 115 = 0

n(n + 23) – 5(n + 23) = 0

(n + 23)(n – 5) = 0

Now, n + 23 = 0         and         n – 5 = 0

n = -23        and         n = 5

Since we know that number of terms (n) can’t be negative.

So, n = 5 is the required number of terms.

It means 5 terms must be taken so that their sum is 115.            Ans.

Example 4) Find the sum of the first n positive integers.

Solution – We know that the positive integers are   1, 2, 3, 4,………………..n

Here first term (a) = 1, last term ( l ) = n,   S_n = ?

Here the last term is given so we shall use the formula S_n = n/2[a + l ]

Putting the values, S_n = n/2[1 + n]

Or we can write,    S_n = n(n+1)/2 

This can be used as the formula to find the sum of positive integers if the number of terms (n) is given.

Example 5) Find the sum of the first 10 terms of AP whose n^th term is a_n = 7n – 9.

Solution – Here n^th term    a_n = 7n – 9

First, we shall generate the AP by the n^th term

For n = 1,         a₁ = 7⨯1 – 9 = 7 – 9 = -2

For n = 2,         a₂ = 7⨯2 – 9 = 14 – 9 = 5

For n = 3,         a₃ = 7⨯3 – 9 = 21 – 9 = 12

So, the AP is -2, 5, 12,…………………

first term (a) = -2, common difference (d) = 5 – (-2) = 5 + 2 = 7

Now, by the formula,    S_n = n/2[2a + (n – 1)d]

Sum of first 10 terms,  S₁₀ = 10/2[2⨯(-2) + (10 – 1)7]

S₁₀ = 5[-4 + (9)7]

S₁₀ = 5[-4 + 63]

S₁₀ = 5[59]

S₁₀ = 295

Therefore, the sum of the first 10 terms of the given AP is 295.             Ans.

Example 6) Find the sum of natural numbers that fall between 350 to 1000 which is divisible by 4.

Solution – Between 350 to 1000, numbers divisible by 4 are 352, 356, 360,…………….1000.

This series is an AP with first term (a) = 352, common difference (d) = 356 – 352 = 4

Last term (a_n) = ( l ) = 1000, number of terms (n) =?

To find the sum we need the number of terms (n) so first, we shall find it by the n^th term formula,

a_n = a + (n – 1)d

1000 = 352 + (n – 1)4

1000 – 352 = 4n – 4

648 + 4 = 4n

652 = 4n

652/4 = n

n = 163

It means there are 163 terms between 350 to 1000 which are divisible by 4.

Now, the sum of 163 terms by the formula,    S_n = n/2[a + l ]

S₁₆₃ = 163/2[352 + 1000]

S₁₆₃ = 163/2[1352] = 163⨯676

S₁₆₃ = 110188

So, the sum of 163 terms which is divisible by 4 is 110188.              Ans.

Example 7) Find the first term of an AP whose sum of n terms is given by 3n² – 2n. Also find the sum of the first two terms, 2^nd term, 3^rd term, 11^th term and n^th term.

Solution – Here sum of n terms of an AP,     S_n = 3n² – 2n

For n = 1,     S₁ = 3(1)² – 2⨯1 = 3 – 2 = 1

So, the first term (a) = 1

Now sum of first two terms putting n = 2,  S₂ = 3(2)² – 2⨯2 = 3(4) – 4 = 12 – 4 = 8

So, the sum of the first two terms is 8.

Second term a₂ = S₂ – S₁            [by the formula, a_n = S_n – S_{n – 1}]

a₂ = 8 – 1

a₂ = 7

So, the 2^nd term is 7.

In the question, it is given AP so the common difference will be the same.

Common difference of first two terms d = a₂ – a₁ = 7 – 1 = 6

So, the 3^rd term will be       a₃ = a₂ + d = 7 + 6 = 13

3^rd term       a₃ = 13

Now the AP: 1, 7, 13,…………..

So, n^th term    a_n = a + (n – 1)d

a_n = 1 + (n – 1)6

a_n = 1 + 6n – 6

n^th term    a_n = 6n – 5 

For n = 11,    a₁₁ = 6⨯11 – 5

a₁₁ = 66 – 5

So,  11^th term      a₁₁ = 61              Ans.

Sum of First n Terms of an Arithmetic Progression Class 10^th in Hindi

More About Sum of First n Terms of an Arithmetic Progression