Area of Triangle in Coordinate Geometry Class 10th

Introduction

Before finding the Area of a Triangle in Coordinate Geometry, We know the area of a triangle if its Base and Height are given

Area of triangle = ½⨯Base⨯Height

If all three sides of a triangle are given then the area of the triangle by Heron’s formula

Area of triangle = √s(s-a)(s-b)(s-c)                    

Where, s = semi-perimeter of the triangle

s = a+b+c/2

a,b,c = three sides of triangle

Derivation of Formula

In coordinate geometry, if coordinates of all three vertices of a triangle are given then we can calculate the area of that triangle. Let us see how it is possible.

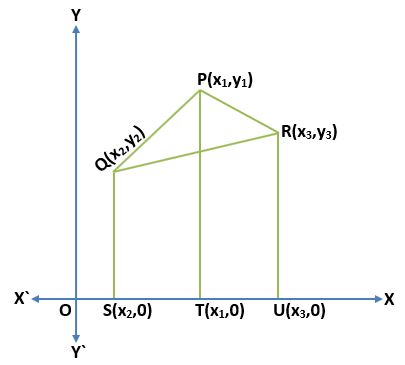
Let PQR be a triangle whose vertices are P(x₁,y₁), Q(x₂,y₂), and R(x₃,y₃). We have drawn perpendiculars QS, PT, and RU from the points Q, P, and R respectively on the x-axis. In the figure, we can see that there are three trapezium PQST, PRUT, and QSUR.

Here, ST = x₁ – x₂, TU = x₃ – x₁, SU = x₃ – x₂

QS = y₂, PT = y₁, RU = y₃

So, we can write,

area of triangle PQR = (area of trapezium PQST + area of trapezium PRUT) – area of trapezium QSUR  —————(1)

We know that area of trapezium = ½⨯(sum of parallel sides)⨯(distance between them)

Now area of trapezium PQST = ½⨯(QS+PT)⨯ST

= ½⨯(y₂ + y₁)⨯(x₁ – x₂)

= ½(x₁y₂ – x₂y₂ + x₁y₁ – x₂y₁)  ——————–(2)

Area of trapezium PRUT = ½⨯(PT+RU)⨯TU

= ½⨯(y₁+y₃)⨯(x₃ – x₁)

= ½(x₃y₁ – x₁y₁ + x₃y₃ – x₁y₃)  ———————(3)

Area of trapezium QSUR = ½⨯(QS+RU)⨯SU

= ½ ⨯(y₂+y₃)⨯(x₃ – x₂)

= ½ (x₃y₂ – x₂y₂ + x₃y₃ – x₂y₃)  ———————(4)

From equations (1), (2), (3) and (4)

Area of triangle PQR = ½(x₁y₂ – x₂y₂ + x₁y₁ – x₂y₁) + ½(x₃y₁ – x₁y₁ + x₃y₃ – x₁y₃) – ½(x₃y₂ – x₂y₂ + x₃y₃ – x₂y₃)

= ½[x₁y₂ – x₂y₂ + x₁y₁ – x₂y₁ + x₃y₁ – x₁y₁ + x₃y₃ – x₁y₃ – x₃y₂ + x₂y₂ – x₃y₃ + x₂y₃]

= ½[x₁y₂ – x₂y₁ + x₃y₁ – x₁y₃ – x₃y₂ + x₂y₃]

= ½[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]

Thus,  area of triangle PQR = ½[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]

Look at Some Examples

Example 1) Find the area of a triangle whose vertices are (-1,1), (6,-4), and (-5,-3).

Solution – Here, the vertices of the triangle are (-1,1), (6,-4), and (-5,-3).

So,  x₁ = -1, y₁ = 1, x₂ = 6, y₂ = -4, x₃ = -5, y₃ = -3

By the formula,

area of triangle  = ½[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]

= ½[-1{-4 – (-3)} + 6(-3 – 1) + (-5){1 – (-4)}]

= ½[-1{-4 + 3} + 6(-4) + (-5){1 + 4}]

= ½[-1{-1} + (-24) + (-5){5}]

= ½[1 – 24 – 25] = ½[1 – 49] = ½[- 48] = -24 square units

Since the area is a positive quantity, that can’t be negative. So we shall take positive measures only.

Therefore, the area of the triangle = 24 square units            Ans.

Example 2) Find the area of the triangle ABC made by vertices A(2,5), B(7,4), and C(-4,7).

Solution – Here,  x₁ = 2, y₁ = 5, x₂ = 7, y₂ = 4, x₃ = -4, y₃ = 7

Now area of triangle ABC = ½[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]

= ½[2(4 – 7) + 7(7 – 5) + (-4)(5 – 4)]

= ½[2(– 3) + 7(2) + (-4)(1)]

= ½[– 6 + 14 – 4]

= ½[4] = 2 square units

So, the area of triangle ABC = 2 square units.             Ans.

Example 3) The vertices of a triangle are (3,2), (0,4), and (-3,6). Find its area.

Solution – Here,  x₁ = 3, y₁ = 2, x₂ = 0, y₂ = 4, x₃ = -3, y₃ = 6

Area of triangle = ½[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]

= ½[3(4 – 6) + 0(6 – 2) + (-3)(2 – 4)]

= ½[3(– 2) + 0 + (-3)(– 2)]

= ½[– 6 + 6] = ½[0] = 0

Here, the area of the triangle is 0 which means the three vertices given in the question do not make a triangle or we can say that the given points are collinear.          Ans.

Note – If three points are given and we have to check that they are collinear or not then we can check this with the help of the area of the triangle formula. If the area of a triangle is zero (0) it means the given three points are collinear and if the area of a triangle is not zero(≠0) it means the given three points are non-collinear. 

Example 4) Check whether the three points (-1,2), (-2,3) and (-3,4) are collinear or not.

Solution – To check whether three points (-1,2), (-2,3), and (-3,4) are collinear or not we shall find that they form a triangle or not with the help of the area of the triangle formula.

Here,  x₁ = -1, y₁ = 2, x₂ = -2, y₂ = 3, x₃ = -3, y₃ = 4

Area of triangle = ½[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]

= ½[-1(3 – 4) + (-2)(4 – 2) + (-3)(2 – 3)]

= ½[-1(– 1) + (-2)(2) + (-3)( – 1)]

= ½[1 – 4 + 3] = ½[0] = 0

Since the area of the triangle formed by the given three points is 0 so these points are collinear.         Ans.

Example 5) Find the value of P if the points (2,-1), (P,-2), and (4,-3) are collinear.

Solution – Since points (2,-1), (P,-2), and (4,-3) are collinear so the area of the triangle formed by these points will be 0.

Here,       x₁ = 2, y₁ = -1, x₂ = P, y₂ = -2, x₃ = 4, y₃ = -3  

∵ Area of triangle = 0

½[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] = 0

½[2{-2 – (-3)} + P{-3 – (-1)} + 4{-1 – (-2)}] = 0

½[2{-2 + 3} + P{-3 + 1} + 4{-1 + 2}] = 0

½[2{1} + P{-2} + 4{1}] = 0

½[2 – 2P + 4] = 0

½[6 – 2P] = 0

6 – 2P = 0

6 = 2P

6/2 = P

P = 3

Therefore, the value of P is 3.             Ans.

Some Questions Based on it

Q 1) Write the formula to find the area of a triangle if its vertices are given.

Ans. – Area of a triangle = ½[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]

Q 2) How can we check that the three points are collinear or not with the help of the area of a triangle?

Ans. – If the area of the triangle formed by that three points is zero (0) then we can say that the three points are collinear and if the area of a triangle is not zero(≠0) then the three points are non–collinear.

Q 3) What are collinear and non-collinear points?

Ans. – Collinear Points – If three or more points lie on a straight line, they are called collinear points.

Non-collinear Points – If three or more points do not lie on a straight line, they are called non–collinear points.

Area of Triangle in Coordinate Geometry Class 10^th in Hindi

More About Area of Triangle in Coordinate Geometry