Introduction
The Pythagoras theorem is given by the Greek mathematician Pythagoras. Before Pythagoras, this theorem was discovered by Indian mathematician Boudhayana so this theorem is also known as Boudhayana Theorem. This theorem is also called Pythagorean Theorem.
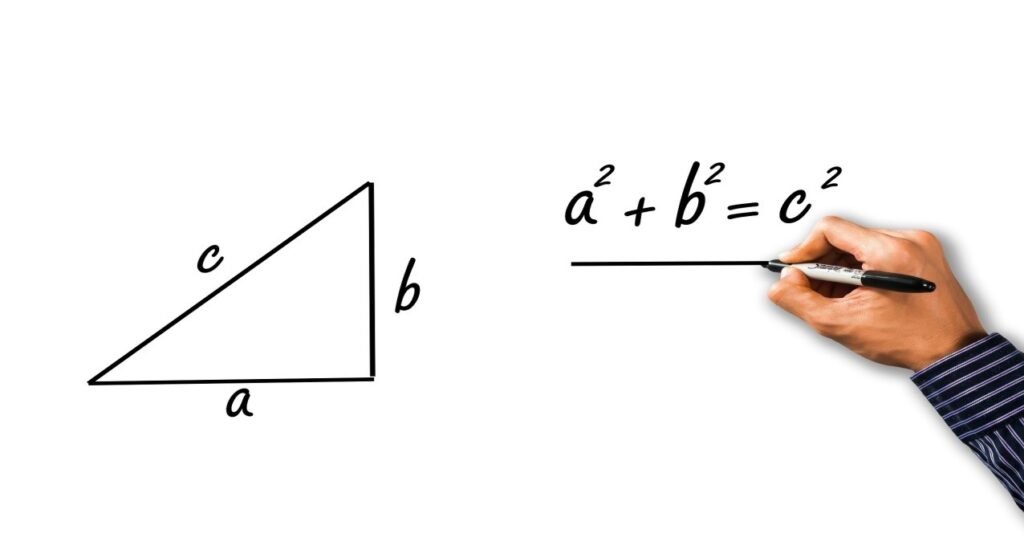
Statement – According to this theorem, In a right-angled triangle, the square of the hypotenuse side is equal to the sum of the square of the base side and perpendicular side.
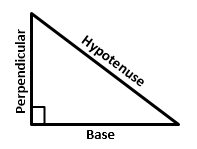
Formula – (Hypotenuse)2 = (Base)2 + (Perpendicular)2
We can also write, H2 = B2 + P2
Note – This theorem can be used for right-angled triangles only.
How is it Used, Let us See –
Pythagoras theorem is used to find any side of a right-angled triangle when the remaining two sides are given.
Example – In a right-angled triangle, the base is 4 cm and the perpendicular is 3 cm then find its hypotenuse side.
Solution – Here, Base(B) = 4 cm , Perpendicular(P) = 3cm and Hypotenuse(H) = ?
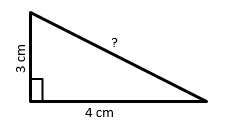
By Pythagoras theorem, H2 = B2 + P2
H2 = (4)2 + (3)2
H2 = 16 + 9
H2 = 25
H = √25
H = 5 cm
Therefore, Hypotenuse is 5 cm. Ans.
Proofs of Pythagoras Theorem
(1) In a right-angled triangle, the area of the square made on the hypotenuse is equal to the sum of the areas of the squares made on the other two sides.
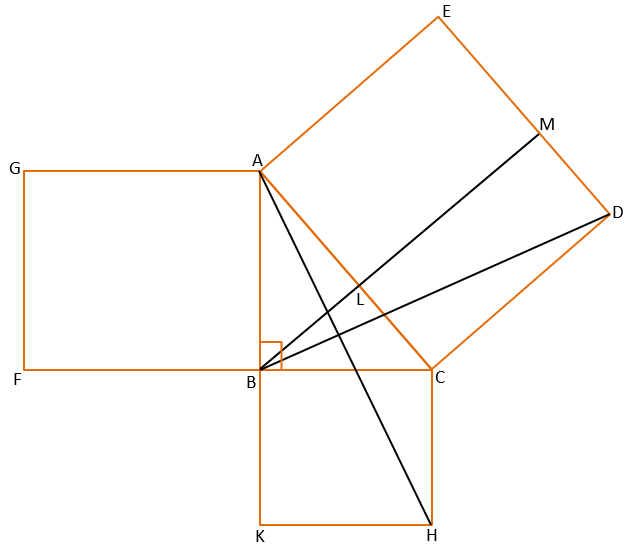
Given – In ∆ABC, ∠B = 90° and squares ACDE, ABFG, and BCHK are made on sides AC, AB, and BC respectively.
To Prove – ar(ACDE) = ar(ABFG) + ar(BCHK) (ar = Area)
Construction – Drawn BM⊥DE and Joined AH and BD.
Proof – ∠ACD = ∠BCH = 90° (Angles of squares)
Adding ∠ACB on both sides
∠ACD + ∠ACB = ∠BCH + ∠ACB
∠BCD = ∠ACH —————-(1)
In ∆ACH and ∆DCB
AC = CD (Sides of square ACDE)
CH = BC (Sides of square BCHK)
∠ACH = ∠BCD (From equation (1)
By SAS congruency criterion
∆ACH ≅ ∆DCB
∴ ar(∆ACH) = ar(∆DCB) (areas of congruent triangles are equal) —————-(2)
∵ ∠ABC = ∠CBK = 90°
∴ ∠ABC + ∠CBK = 180°
It means ABK is a straight line.
∵ CH ∥ BK
∴ CH ∥ AK
∵ ∆ACH and square BCHK are made on the same base CH and between the same parallel lines AK and CH
∴ ar( ∆ACH) = ½ ar (square BCHK) —————(3)
Similarly, ∆DCB and Rectangle CDML are made on the same base CD and between the same parallel lines CD and BM
∴ ar( ∆DCB) = ½ ar (rectangle CDML) —————-(4)
From equations (2), (3) and (4) we get
ar(∆ACH) = ar(∆DCB)
½ ar (square BCHK) = ½ ar (rectangle CDML)
ar (square BCHK) = ar (rectangle CDML) —————-(5)
Similarly, ar(square ABFG) = ar(rectangle AEML) —————–(6)
Adding equations (5) and (6),
ar (square BCHK) + ar(square ABFG) = ar (rectangle CDML) + ar(rectangle AEML)
ar (square BCHK) + ar(square ABFG) = ar (square ACDE)
or ar (square ACDE) = ar (square BCHK) + ar(square ABFG) Hence Proved.
(2) In a right-angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the remaining two sides.
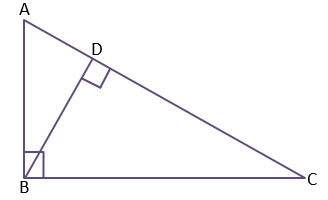
Given – In ∆ABC, ∠B = 90°
To Prove – AC2 = AB2 + BC2
Construction – Drawn BD ⊥ AC
Proof – In ∆ABC and ∆ADB
∠ABC = ∠ADB (Both are 90°)
∠BAC = ∠DAB (Common angle in both triangles)
By AA similarity criterion, ∆ABC ∼ ∆ADB
Therefore, AB ∕ AD = AC ∕ AB (By Thales theorem)
AB2 = AC⨯AD —————-(1)
Now in ∆ABC and ∆BDC
∠ABC = ∠BDC (Both are 90°)
∠ACB = ∠BCD (Common angle in both triangles)
By AA similarity criterion, ∆ABC ∼ ∆BDC
Therefore, BC / DC = AC / BC (By Thales theorem)
BC2 = AC⨯CD —————-(2)
By adding equations (1) and (2),
AB2 + BC2 = AC⨯AD + AC⨯CD
AB2 + BC2 = AC (AD + CD)
AB2 + BC2 = AC⨯AC
AB2 + BC2 = AC2
AC2 = AB2 + BC2 Hence Proved.
Some Other Examples of Pythagoras Theorem
Example 1) In a right-angled triangle, Hypotenuse is 7 cm and the perpendicular is 4 cm then find its Base.
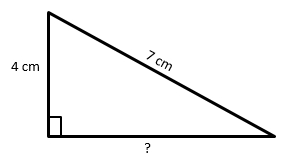
Solution – By Pythagoras theorem,
H2 = B2 + P2
(7)2 = B2 + (4)2
49 = B2 + 16
49 – 16 = B2
B2 = 33
B = √33
B = 5.74 cm Ans.
Example 2) Length and breadth of a rectangle are 5 cm and 7 cm. find its diagonal.
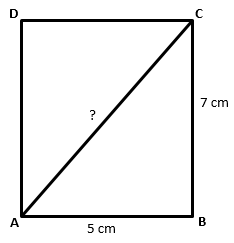
Solution – Because of the diagonal, this Rectangle is divided into two right-angled triangles.
So, by Pythagoras theorem, in ∆ABC
AC2 = AB2 + BC2
AC2 = (5)2 + (7)2
AC2 = 25 + 49
AC2 = 74
AC = √74
AC = 8.60 cm
Therefore, the length of the diagonal is 8.60 cm. Ans.
