Introduction
In Coordinate Geometry, in a plane, there are two points whose coordinates are given and are joined by a line and there is also a third point which is situated on the line joining the two points. The third point divides the line into two parts or sections and we have to find the coordinates of the third point. If we know the ratio of the two sections and the coordinates of the two points then we can easily find out the coordinates of the third point situated on the line joining the two points by Section Formula.
In this there are two conditions, the first being that the third point can be situated in the interior part (on the line joining the two points) which is called the Internal Division and the second is that the third point can be situated in the exterior part (in the left or in the right of both the points) which is called the External Division.
Internal Division of the Distance Between Two Points
Suppose there are two points A(x1,y1) and B(x2,y2) situated in a plane, and a third point P(x,y) divides the line joining the two points in the ratio m1 ∶ m2 internally.
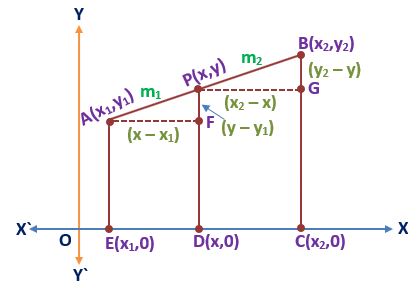
We draw perpendicular AE, BC, and PD on the x–axis from points A, B, and P respectively. We also draw perpendicular AF and PG on PD and BC respectively. From the figure,
OE = x1, OD = x, OC = x2, AE = FD = y1, PD = GC = y, BC = y2
Therefore, AF = ED = x – x1, PG = DC = x2 – x,
PF = PD – FD = y – y1, BG = BC – GC = y2 – y
And PA/PB = m1/m2
In △AFP and △PGB,
∠APF = ∠PBG [Corresponding angles are equal, because PD⊥OX and BC⊥OX, PD∥BC]
∠PAF = ∠BPG [Corresponding angles are equal, because AF⊥PD and PG⊥BC, AF∥PG]
∠AFP = ∠PGB = 90° [AF⊥PD and PG⊥BC]
So, by the AAA similarity criterion, △AFP ∼ △PGB
Therefore, PA/BP = AF/PG = PF/BG
Putting the values from above
m1/m2 = (x – x1)/(x2 – x) = (y – y1)/(y2 – y)
Here, m1/m2 = (x – x1)/(x2 – x) and m1/m2 = (y – y1)/(y2 – y)
Solving by cross multiply,
m1(x2 – x) = m2(x – x1) and m1(y2 – y) = m2(y – y1)
m1x2 – m1x = m2x – m2x1 and m1y2 – m1y = m2y – m2y1
m1x2 + m2x1 = m2x+ m1x and m1y2 + m2y1 = m2y+ m1y
m1x2 + m2x1 = x(m2 + m1) and m1y2 + m2y1 = y(m2 + m1)
(m1x2 + m2x1)/(m2 + m1) = x and (m1y2 + m2y1)/(m2 + m1) = y
Or x = (m1x2 + m2x1)/(m1 + m2) and y = (m1y2 + m2y1)/(m1 + m2)
The above value of x and y are the required coordinates of point P which divides the line segment AB in the ratio m1 ∶ m2 internally.
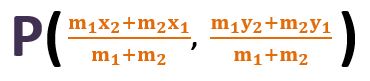
The value of x and y is called the Section Formula for Internal Division.
External Division of the Distance Between Two Points
Let there be two points A(x1,y1) and B(x2,y2) situated in a plane and a third point P(x,y) divides the line joining the two points in the ratio m1 ∶ m2 externally.
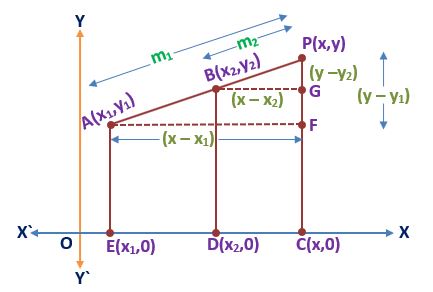
We draw perpendicular AE, BD, and PC on the x–axis from points A, B, and P respectively. We also draw perpendicular AF and BG from points A and B on the PC. From the figure,
OE = x1, OD = x2, OC = x, AE = FC = y1, BD = GC = y2, PC = y
Therefore, AF = EC = x – x1, BG = DC = x – x2,
PF = PC – FC = y – y1, PG = PC – GC = y – y2
And PA/PB = m1/m2
In △AFP and △BGP,
∠APF = ∠BPG [Common angles]
∠PAF = ∠PBG [Corresponding angles are equal, because AF⊥PC and BG⊥PC, AF∥BG]
∠AFP = ∠BGP = 90° [AF⊥PC and BG⊥PC]
So, by the AAA similarity criterion, △AFP ∼ △BGP
Therefore, PA/PB = AF/BG = PF/PG
Putting the values from above
m1/m2 = x – x1/x – x2 = y – y1/y – y2
Here, m1/m2 = x – x1/x – x2 and m1/m2 = y – y1/y – y2
Solving by cross multiply,
m1(x – x2) = m2(x – x1) and m1(y – y2) = m2(y – y1)
m1x – m1x2 = m2x– m2x1 and m1y – m1y2 = m2y– m2y1
m1x – m2x = m1x2 – m2x1 and m1y- m2y = m1y2 – m2y1
x(m1 – m2) = m1x2 – m2x1 and y(m1 – m2) = m1y2 – m2y1
x = (m1x2 – m2x1)/(m1 – m2) and y = (m1y2 – m2y1)/(m1 – m2)
The above value of x and y are the required coordinates of point P which divides the line segment AB in the ratio m1 ∶ m2 externally.
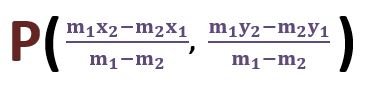
The value of x and y is called the Section Formula for External Division.
Note – 1) In the internal division, If point P is situated in the middle of the line segment AB then it will divide the line segment in the equal ratio as 1 ∶ 1, then coordinates of the mid-point P will be
x = (1⨯x2 + 1⨯x1)/1+1 and y = (1⨯y2 + 1⨯y1)/1+1
x = (x2 + x1)/2 and y = (y2 + y1)/2
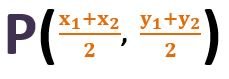
2) In the external division, if m1 > m2 then point P will be situated on the right of both points A and B, And if m2 > m1 then point P will be situated on the left of both points A and B.
3) The internal division formula can be converted into the External division formula by just replacing the +ve sign with the –ve sign.
4) If point P divides the line segment AB in the ratio which is not known then we can assume the ratio as k ∶ 1 then the coordinates of point P will be [(kx2 + x1)/k+1, (ky2 + y1)/k+1]
Some Examples –
Example 1) Find the coordinates of the point which divides the line segment joining the points (-2,5) and (3,4) in the ratio 3 ∶ 5 internally.
Solution – Let P(x,y) be the required point that divides the line segment joining the points A(-2,5) and B(3,4). We can understand it by figure.
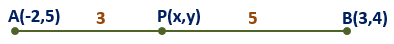
Here, x1 = -2, y1 = 5, x2 = 3, y2 = 4, m1 = 3, m2 = 5
By section formula for internal division,
x = (m1x2 + m2x1)/(m1 + m2) and y = (m1y2 + m2y1)/(m1 + m2)
Putting the values, x = {3⨯3 + 5⨯(-2)}/(3 + 5) and y = (3⨯4 + 5⨯3)/(3 + 5)
x = {9 + (-10)}/8 and y = (12 + 15)/8
x = {9 – 10}/8 and y = 27/8
x = -1/8 and y = 27/8
So, the required coordinates are (-1/8, 27/8). Ans.
Example 2) Find the coordinates of the point which externally divides the line segment joining the points (-1,-2) and (-2,4) in the ratio 3 ∶ 2.
Solution – Let the required point be P(x,y).

Here, x1 = -1, y1 = -2, x2 = -2, y2 = 4, m1 = 3, m2 = 2
By section formula for external division,
x = (m1x2 – m2x1)/(m1 – m2) and y = (m1y2 – m2y1)/(m1 – m2)
Putting the values, x = {3⨯(-2) – 2⨯(-1)}/(3 – 2) and y = {3⨯4 – 2⨯(-2)}/(3 – 2)
x = {-6 + 2}/1 and y = {12 + 4}/1
x = -4 and y = 16
So, the coordinates of the required point are (-4,16). Ans.
Example 3) In which ratio does the y-axis divide the line segment joining the points (-4,1) and (2,2)?
Solution – We know that the coordinates of a point situated on the y–axis are of the form (0,y).
So, let point P(0,y) internally divides the line segment joining the points (-4,1) and (2,2) in the ratio m1 ∶ m2.
Here, we shall use the section formula for the internal division for x – coordinate only because it is zero for point P.
x1 = -4, y1 = 1, x2 = 2, y2 = 2
By section formula for internal division, x = (m1x2 + m2x1)/(m1 + m2)
0 = m1⨯2 + m2⨯(-4)/(m1 + m2)
0 = 2m1 – 4m2
4m2 = 2m1
4/2 = m1/m2
m1/m2 = 2/1
Therefore, the ratio is m1 ∶ m2 = 2 ∶ 1. Ans.
Example 4) In which ratio does point (4,5) externally divide the line segment joining points (3,1) and (2,-6)?
Solution – Let the ratio be k ∶ 1 and point P(4,5) externally divides the line segment joining the points A(3,1) and B(2,-6).
Here, x1 = 3, y1 = 1, x2 = 2, y2 = -6, x = 4, y = 5, m1 = k, m2 = 1
So, by section formula for external division, x = (m1x2 – m2x1)/(m1 – m2)
4 = (k⨯2 – 1⨯3)/(k – 1)
4(k – 1) = 2k – 3
4k – 4 = 2k – 3
4k – 2k = – 3 + 4
2k = 1
k/1 = ½
Hence, the ratio is k ∶ 1 = 1 ∶ 2. Ans.
Note – 1) In the above example, we can also use y – coordinate to find the ratio.
2) We can also find the ratio by taking the ratio of Distance PA and PB by using the Distance formula.
Example 5) If point P(4,2) divides the line segment joining the points A(1,2) and B in the ratio 2 ∶ 5 internally then find the coordinates of point B.
Solution – Let the coordinates of point B be (x2,y2).
Here, x = 4, y = 2, x1 = 1, y1 = 2, m1 = 2, m2 = 5
By section formula for internal division,
x = (m1x2 + m2x1)/(m1 + m2) and y = (m1y2 + m2y1)/(m1 + m2)
4 = (2⨯x2 + 5⨯1)/(2 + 5) and 2 = (2⨯y2 + 5⨯2)/(2 + 5)
4 = (2x2 + 5)/7 and 2 = (2y2 + 10)/7
4⨯7 = 2x2 + 5 and 2⨯7 = 2y2 + 10
28 – 5 = 2x2 and 14 – 10 = 2y2
23 = 2x2 and 4 = 2y2
23/2 = x2 and 4/2 = y2
x2 = 23/2 and y2 = 2
Therefore, the coordinates of point B are (23/2, 2). Ans.
Example 6) Find the ratio in which the line 3x + y = 9 divides the line segment which joins the points (1,3) and (2,7).
Solution – Let the line 3x + y = 9 internally divide the line segment joining the points (1,3) and (2,7) at point P(x,y) in the ratio k ∶ 1.
Here, x1 = 1, y1 = 3, x2 = 2, y2 = 7, m1 = k, m2 = 1
Now by section formula, the coordinates of point P will be
x = (m1x2 + m2x1)/(m1 + m2) and y = (m1y2 + m2y1)/(m1 + m2)
x = (k⨯2 + 1⨯1)/(k + 1) and y = (k⨯7 + 1⨯3)/(k + 1)
x = 2k + 1/k+1 and y = 7k + 3/k+1
Since point P lies on line 3x + y = 9 so, it will satisfy it.
3x + y = 9
3(2k + 1/k+1) + (7k + 3/k+1) = 9
{3(2k + 1)+(7k + 3)}/(k+1) = 9 [LCM = (k+1)]
6k + 3 + 7k + 3 = 9(k+1)
13k + 6 = 9k + 9
13k – 9k = 9 – 6
4k = 3
k/1 = ¾
So, the required ratio will be k ∶ 1 = 3 ∶ 4. Ans.