Definition
The polynomial in one variable (like x) with degree 2 is called Quadratic Equation.
Examples – 2x2 + 3x + 5, x2 – 4x + 7, x2 + 8, 3x2 + 9x,…. etc.
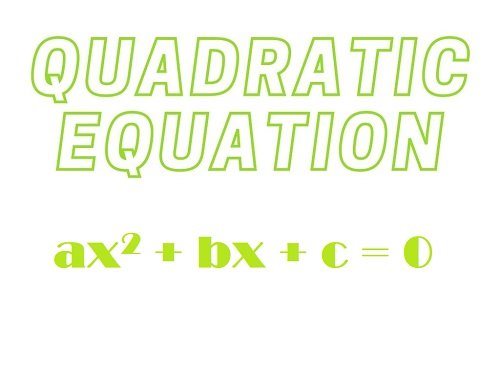
Standard Form of Quadratic Equation
ax2 + bx + c = 0
Where a, b, and c are real numbers and a ≠ 0
x = Variable (unknown)
Some Important Points
- In the quadratic equation, the highest power of variable x is 2 so it is also called the quadratic polynomial.
- The degree of any polynomial shows the number of solutions which are called zeroes or roots.
- In the quadratic equation, the degree is 2 so roots (solutions) will be always two values.
- In any quadratic equation, coefficients b and c can be zero but a can’t be zero because if a = 0 then that polynomial will not be quadratic that will be linear.
Examples –
| 2x2 + 3x + 5 | a = 2, b = 3, c = 5 |
| x2 – 4x + 7 | a = 1(we generally do not write 1x2), b = -4, c = 7 |
| x2 + 8 | a = 1, b = 0, c = 8 |
| 3x2 + 9x | a = 3, b = 9, c = 0 |
Solution of Quadratic Equation
Factorization Method
In this method, we factorize the quadratic equation and put each factor equal to zero and then find the values of x. These values of x are the solution of the quadratic equation and are called the roots of the Quadratic Equation.
This can be understood by the following examples.
Example – 1) Find the roots of the quadratic equation x2 + 5x + 6 = 0 by factorization method.
Solution – given equation x2 + 5x + 6 = 0
Step (1) Comparing the equation with the standard form ax2 + bx + c = 0
a = 1, b = 5, c = 6
We take a⨯c = 1⨯6 = 6 and b = 5
Step (2) Now we have to take two numeric values so that their sum should be equal to b i.e., 5 and their multiplication should be equal to a⨯c i.e., 6. So, we take the numbers 2 and 3.
Note – If it is difficult to find the two numeric values, we can factorize the term a⨯c and make pair to get it easily.
Step (3) now check
2+3 = 5 and 2⨯3 = 6 (these values satisfy)
Step (4) Now break the middle term of equation x2 + 5x + 6 with the help of the above sum 2+3 = 5
x2 + (2+3)x + 6 = 0
x2 + 2x + 3x + 6 = 0
Step (5) Now take common terms out from the first two terms and last two terms.
x(x + 2) + 3(x+2) = 0
(x+2) is again a common term so
(x+2) (x+3) = 0
Step (6) Now, by putting each factor equal to zero.
(x+2) = 0 and (x+3) = 0
x = −2 and x = −3 Ans.
Both the values of x are the solution of the given quadratic equation and are called the roots of this equation.
We can check our answer by putting the values of x in the given quadratic equation.
x2 + 5x + 6 = 0
at x = −2,
(−2)2 + 5(−2) + 6 = 0
4 – 10 + 6 = 0
– 6 + 6 = 0
0 = 0
LHS = RHS
at x = −3,
(−3)2 + 5(−3) + 6 = 0
9 – 15 + 6 = 0
– 6 + 6 = 0
0 = 0
LHS = RHS
At both values, LHS = RHS which means our answer is correct.
Example – 2) Find the roots of the quadratic equation 2x2 – 5x + 3 = 0 by factorization method.
Solution – 2x2 – 5x + 3 = 0 Here, a⨯c = 2⨯3 = 6 and b = −5
2x2 – (2+3)x + 3 = 0 two numeric values −2 and −3
2x2 – 2x − 3x + 3 = 0 −2⨯(−3) = 6 and −2 + (-3) = −2 − 3 = −5
2x(x − 1) − 3(x − 1) = 0
(x − 1) (2x − 3) = 0
(x − 1) = 0 and (2x − 3) = 0
x = 1 and x = 3/2
Thus, the roots of the quadratic equation 2x2 – 5x + 3 = 0 are x = 1 and x = 3/2. Ans.
Perfect The Square Method (Complete The Square Method)
In this method, we convert the quadratic equation into the perfect square form and then we take the square root to obtain the required roots.
This method will be clear by the following examples.
Example – 1) Solve the quadratic equation 9x2 – 3x – 2 = 0 by the perfect square method.
Solution – Given equation 9x2 – 3x – 2 = 0
Step 1) We divide the whole equation by 9 to make 1 as the coefficient of x2.
9x2/9 – 3x/9 – 2/9 = 0
x2 – x/3 – 2/9 = 0
Step 2) Taking the constant term to the right side,
x2 – x/3 = 2/9
Step 3) Adding the square of half of the coefficient of x to both sides to make a perfect square on the left side.
x2 – x/3 + (⅙)2 = 2/9 + (⅙)2 [Half of coefficient of x = ⅓ ÷ 2 = ⅓⨯½ = ⅙]
Step 4) Now the left side is a perfect square
(x – ⅙)2 = 2/9 + 1/36
(x – ⅙)2 = (2⨯4 + 1⨯1)/36 (LCM = 36)
(x – ⅙)2 = 9/36
(x – ⅙)2 = ¼
Easy Tip – To make a perfect square, we put the sign of the middle term (– x/3) of the equation (x2 – x/3 – 2/9 = 0) which in this example is – (negative), between the variable x and half of the coefficient of x which is ⅙, and make a perfect square (x – ⅙)2.
Step 5) By taking the square root of both sides.
√(x – ⅙)2 = √¼
x – ⅙ = ±½
Taking both the values separately,
On taking the (+) sign,
x – ⅙ = +½
x = ½ + ⅙
x = (1⨯3 + 1⨯1)/6
x = 4/6
x = ⅔
On taking the (−) sign,
x – ⅙ = −½
x = −½ + ⅙
x = (−1⨯3 + 1⨯1)/6
x = −2/6
x = −⅓
So, x = ⅔ and x = −⅓ are the required roots of the quadratic equation 9x2 – 3x – 2 = 0. Ans.
Example – 2) Solve the quadratic equation 2x2 – 7x + 3 = 0 by the perfect square method.
Solution – Given equation 2x2 – 7x + 3 = 0
Dividing the equation by 2 to make 1 as the coefficient of x2
2x2/2 – 7x/2 + 3/2 = 0
x2 – 7x/2 + 3/2 = 0
Taking the constant term to the right side
x2 – 7x/2 = –3/2
Adding the square of half of the coefficient of x to both side
x2 – 7x/2 + (7/4)2 = –3/2 + (7/4)2 [Half of coefficient of x = 7/2 ÷ 2 = 7/2⨯½ = 7/4]
(x – 7/4)2 = –3/2 + 49/16 = (–3⨯8 + 49⨯1)/16 = (–24 + 49)/16 = 25/16
(x – 7/4)2 = 25/16
Taking square root on both sides,
√(x – 7/4)2 = √(25/16)
x – 7/4 = ±5/4
On taking the (+) sign,
x – 7/4 = +5/4
x = 5/4 + 7/4
x = (5 + 7)/4 = 12/4
x = 3
On taking the (−) sign,
x – 7/4 = –5/4
x = –5/4 + 7/4
x = (–5 + 7)/4 = 2/4
x = ½
Both the values of the x are the required roots. Ans.
Quadratic Formula (Shridharacharya Sutra)
The quadratic formula is given by the great Indian mathematician Shridharacharya and is also known as Shridharacharya Sutra. This formula is used to solve the quadratic equation.
x = –b ± √(b2 – 4ac)/2a
Where x = variable
a, b, c = Coefficients of quadratic equation
↣ This formula can be derived from the perfect square method.
The standard form of a quadratic equation is
ax2 + bx + c = 0
x2 + bx/a + c/a = 0 (taking 1 as coefficient of x2 or dividing the whole equation by the coefficient of x2 (a))
x2 + bx/a = −c/a (taking the constant term to the right side)
x2 + bx/a + (b/2a)2 = −c/a + (b/2a)2 (adding square of half of coefficient of x)
(x + b/2a)2 = −c/a + b2/4a2
(x + b/2a)2 = (−c⨯4a + b2⨯1)/4a2 = (−4ac + b2)/4a2
Taking square root on both sides,
√(x + b/2a)2 = √(−4ac + b2)/4a2
x + b/2a = ±√(b2 − 4ac)/2a
x = −b/2a ± √(b2 − 4ac)/2a
x = −b ± √(b2 − 4ac)/2a
Here, sign ± shows the two values of x.
x = −b + √(b2 − 4ac)/2a x = −b − √(b2 − 4ac)/2a
The above values of x are the Shridharacharya Sutra.
Example – Solve the quadratic equation 9x2 + 7x – 2 = 0 by Shridharacharya sutra.
Solution – given equation 9x2 + 7x – 2 = 0
Comparing with standard form ax2 + bx + c = 0
So, a = 9, b = 7, c = – 2
By quadratic formula, x = −b ± √(b2 − 4ac)/2a
Putting the values of a, b, c
x = −7 ± √{72 − 4⨯9⨯(-2)}/2⨯9
x = −7 ± √{49 + 72}/18
x = −7 ± √{121}/18 = −7 ± 11/18
On taking the (+) sign,
x = −7 + 11/18
x = 4/18
x = 2/9
On taking the (−) sign,
x = −7 − 11/18
x = −18/18
x = −1
These values of x are the roots of the given quadratic equation. Ans.
Discriminant and Nature of Roots
We can find the nature of roots by the term b2 – 4ac used in the Shridharacharya sutra which is called the discriminant. It is denoted by D.
D = b2 – 4ac
⇒ If D > 0 then the roots will be different and real.
x = (−b + √D)/2a and x = (−b − √D)/2a
⇒ If D = 0 then the roots will be equal and real.
x = −b/2a and x = −b/2a
⇒ If D < 0 then the roots will not be real, they will be imaginary.
Example – 1) find the nature of the roots of equation 2x2 – 6x + 3 = 0 and if roots exist then find them.
Solution – Given equation 2x2 – 6x + 3 = 0
Comparing the equation with ax2 + bx + c = 0
Here, a = 2, b = – 6, c = 3
Now D = b2 – 4ac
D = (-6)2 – 4⨯2⨯3 = 36 – 24 = 12
∵ D > 0
∴ The roots of equation 2x2 – 6x + 3 = 0 will be different and Real.
By Shridharacharya formula, x = (−b ± √D)/2a where, D = b2 – 4ac
x = {−(-6) ± √12)}/2⨯2 = {6 ± √(4⨯3)}/4
x = {6 ± 2√3}/4 = 2{3 ± √3}/4 = {3 ± √3}/2
So, the roots are x = (3 + √3)/2 and x = (3 − √3)/2. Ans.
Example – 2) find the nature of roots of the equation x2 – 4x + 4 = 0 and if roots exist then find them.
Solution – Given equation x2 – 4x + 4 = 0
By comparing with ax2 + bx + c = 0
Here, a = 1, b = – 4, c = 4
Now D = b2 – 4ac
D = (-4)2 – 4⨯1⨯4 = 16 – 16 = 0
∵ D = 0
∴ The roots of the equation x2 – 4x + 4 = 0 will be equal and Real.
By quadratic formula, x = (−b ± √D)/2a where, D = b2 – 4ac
x = {−(-4) ± √0)/2⨯1 = (4 ± 0)/2 = 4/2
x = 2
So, the roots are x = 2 and x = 2. Ans.
Example – 3) find the nature of the roots of equation 2x2 + 3x + 5 = 0 and if roots exist then find them.
Solution – Given equation 2x2 + 3x + 5 = 0
On comparing with ax2 + bx + c = 0
a = 2, b = 3, c = 5
Now D = b2 – 4ac
D = (3)2 – 4⨯2⨯5 = 9 – 40 = –31
∵ D < 0
∴ The roots of equation 2x2 + 3x + 5 = 0 will not be Real. They will be imaginary.
By Shridharacharya quadratic formula, x = (−b ± √D)/2a where, D = b2 – 4ac
x = (−3 ± √-31)/2⨯2 = (−3 ± √−1⨯31)/4
x = (−3 ± √−1⨯√31)/4 = (−3 ± √31i )/4
So, the roots x = (−3 + √31i )/4 and x = (−3 − √31i )/4. where, i(iota) = √−1

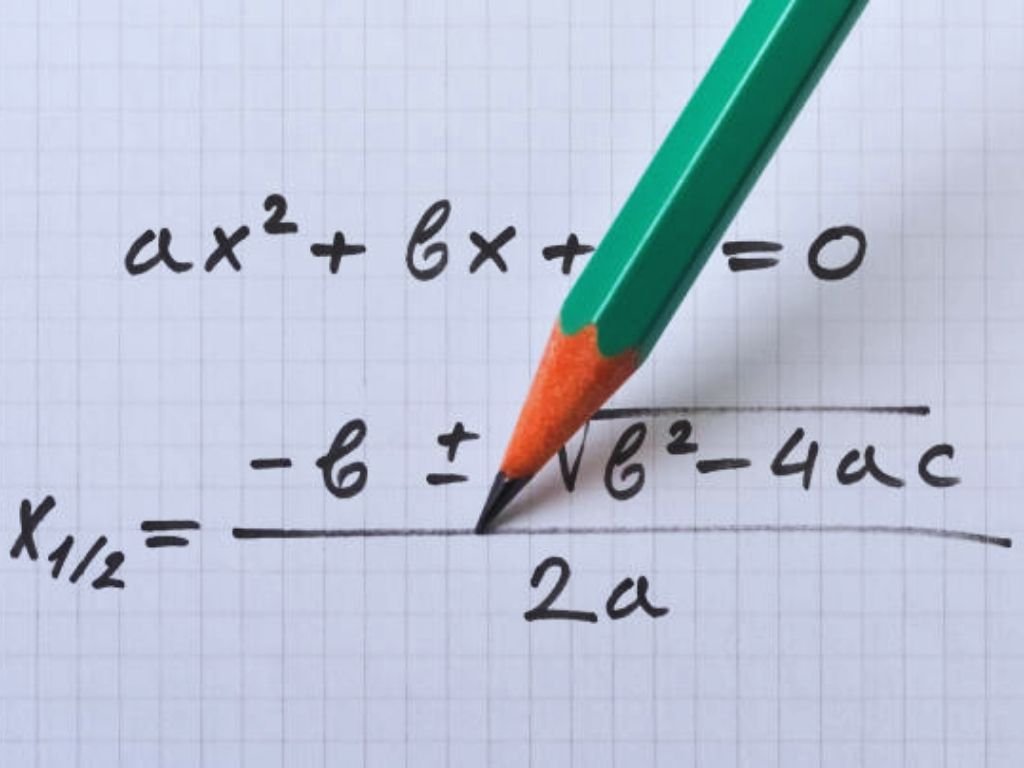























































































































































Hi, after reading this remarkable post i am as well cheerful to share my know-how here with
mates.
I couldn?t resist commenting. Exceptionally well written!|
Amazing work keep it up
Your article helped me a lot, is there any more related content? Thanks! https://accounts.binance.com/fr/register-person?ref=GJY4VW8W
What’s up, just wanted tto mention, I liked this post.
It was inspiring. Keep on posting!
If you are going for finest contents like myself, only go
to see this web site daily since it provides quality contents, thanks
Hi, its pleasant piece of writing concerning media print, we all know media is a wonderful source of
facts.
Valuable information. Fortunate me I discovered your web
site by chance, and I’m shocked why this coincidence didn’t took place in advance!
I bookmarked it.