Integers Class 6th

Introduction

In the number system, we have studied natural numbers and whole numbers. Now in class 6^th, we shall study negative numbers also. We know that whole numbers are positive numbers along with zero (0). If we put positive numbers, negative numbers, and zero (0) together, the collection of these types of numbers is called integers.

……… -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 ………

Definition

The whole numbers and the negative numbers together are called integers.

Or

All the positive and negative numbers along with zero are called integers.

Integers are denoted by Z. In integers, positive numbers are called positive integers and negative numbers are called negative integers. Positive integers are denoted by Z⁺ and negative integers are denoted by Z^–.

Integers Z = {……. -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6 …….}

Positive integers Z⁺ = {1, 2, 3, 4, 5, 6 ………….}

Negative integers Z^– = {-1, -2, -3, -4, -5, -6 …………}

Important Points

• Integers are the real numbers.
• Integers include natural numbers and whole numbers.
• 0 is neither a negative integer nor a positive integer, it is neutral.
• Integers do not include fractions and decimal numbers. Like 5.6, 7/9, etc.

Predecessor and Successor of Integers

Predecessor – if we subtract 1 from any number, we get the predecessor of that number. For integers, every number has its predecessor.

Examples – Predecessor of 2 = 2 – 1 = 1

Predecessor of -11 = -11 – 1 = -12

Successor – if we add 1 to any number, we get the successor of that number. For integers, every number has its successor.

Examples – Successor of 0 = 0 + 1 = 1                    

Successor of -56 = -56 + 1 = -55

Integers on The Number Line

If we draw a line and mark 0 on it then positive integers are marked on the right side of zero (0) and negative integers are marked on the left side of zero (0). This line is the number line for integers.

Representation of Integers on Number Line

To represent any number on the number line first, we draw the number line with both positive and negative integers. Then according to the sign of that number, we represent the number either on the right side or left side. Let’s take an example.

Example – Represent 8 and -5 on the number line.

Solution – 8 = positive integer = right side of zero (0)                  

–5 = negative integer = left side of zero (0)

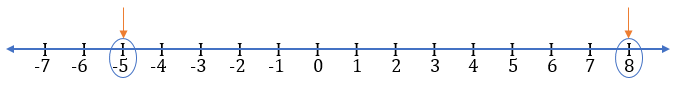
To represent 8, we move 8 steps to the right side of zero because of a positive integer, and to represent -5, we move 5 steps to the left side of zero because of a negative integer.

Addition of Integers on Number Line

1) If we have to add two positive integers then that is the same as the addition of two whole numbers. The result of the addition of two positive integers will be on the right side of both integers. Let’s understand with the help of an example.

Addition of integers 3 and 4

To add 3 and 4, first, we move 3 steps to the right side from 0 and reach number 3. From number 3 we again move 4 steps to the right side and reach number 7. Therefore, the addition is 7.

3 + 4 = 7

2) If we have to add two negative integers then the result will be on the left side of both integers.

Addition of -2 and -3

To add -2 and -3, first, we move 2 steps to the left side from 0 and reach number -2. From -2 we again move 3 steps to the left side and reach number -5. Therefore, the addition is -5.

-2 + (-3) = -5

3) If we have to add a positive integer and a negative integer then for a positive integer we move to the right side and for a negative integer, we move to the left side.

Addition of -1 and 4

To add -1 and 4, first, we move 1 step to the left side from 0 and reach -1. From -1 we again move 4 steps to the right side and reach number 3. Therefore, the addition is 3.

-1 + 4 = 3

Addition of 5 and -7

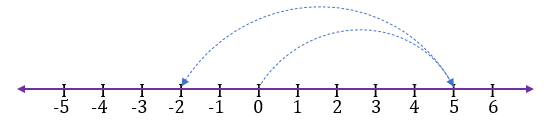
To add 5 and -7, first, we move 5 steps to the right side from 0 and reach 5. From 5 we move 7 steps to the left side and reach number -2. Therefore, the addition is -2.

5 + (-7) = -2

Addition of -4 and 4

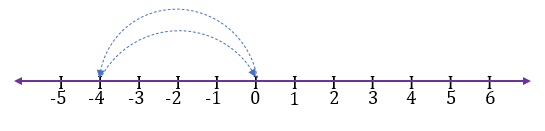
To add -4 and 4, first, we move 4 steps to the left side from 0, and then from -4 we again move 4 steps to the right side and reach number 0. Therefore, the addition is 0.

It means the addition of the same number with a different sign is always 0. These types of numbers are called Additive inverse of each other.

Subtraction of Integers on Number Line

In the subtraction of an integer from another integer, the additive inverse of the integer to be subtracted is added to the other number. The addition of an additive inverse to the other number is the same as the addition of two integers. Let’s take some examples.

1) Subtraction of 3 from 7

Additive inverse of 3 = -3     

Now 7 + (-3) = 4

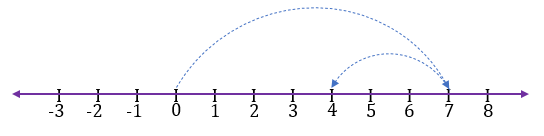
2) Subtraction of -2 from 6

Additive inverse of -2 = 2     

Now 6 + 2 = 8

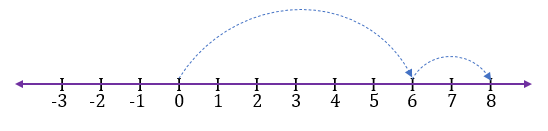
3) Subtraction of 4 from -3

Additive inverse of 4 = -4     

Now -3 + (-4) = -7

4) Subtraction of -1 from -2

Additive inverse of -1 = 1     

Now -2 + 1 = -1

Operation on Integers

Addition of Integers

1) Addition of two positive integers – the addition of two positive integers is the same as the addition of two whole numbers. When we add two positive integers the result is always a greater positive integer.

Examples – 1) 4 + 5 = 9

2) 1 + 6 = 7

2) Addition of two negative integers – in the addition of two negative integers, we simply add both numbers but with the negative sign (-). When we add two negative integers the result is always a smaller negative integer.

Examples – 1) -2 + (-3) = -(2 + 3) = -5

2) -9 + (-7) = -(9 + 7) = -16

3) Addition of a positive integer and a negative integer – in the addition of a positive integer and a negative integer, we generally subtract the smaller number from the greater number and in the result, we put the sign of the greater number.

Examples – 1) -8 + 5 = -(8 – 5) = -3 (the greater number is 8 so we put – in the result)

2) +10 – 3 = +(10 – 3) = +7 (greater number is 10 so we put + in the result)

3) -2 + 9 = +(9 – 2) = +7 (greater number is 9 so we put + in the result)

Integers Class 6^th in Hindi

More About Integers