Introduction
We are familiar with algebraic expressions and equations because we have already studied these in the previous class. Algebraic expressions are mathematical expressions that have a combination of numbers and the English alphabet letters. In the equations, there is the equality sign (=) that is not used in algebraic expressions.
Some examples of algebraic expressions and equations.
Algebraic Expressions – 2x + 3, 3xz – y + z, 6x2, y2 – 1 + x, x + y + z
Equations – x + 5 = 1, 7y = 49, 2x + y = 8, 6x2 – 1 = 0, 9t/3 = 10
In the above examples of algebraic expressions and equations, some have more than one variable and some have a value of the degree more than 1. We have to study linear equations in one variable in this class. Which types of equations are linear equations and what are the conditions for linear equations in one variable? Let’s elaborate on this.
What are Linear Equations in one variable?
The equation which contains only one variable and has the value of degree only 1 is called the linear equation in one variable. The value of the degree of the equation should be 1 which means the power of the variable used in the equation should be 1.
Examples – 1) 4x + 8 = 2
2) 7y = 0
3) 2z – 1 = 9
4) 5 – 3x = 0
5) x + 6 = 7
With the help of the above examples, we can make the general form of the linear equations in one variable which is ax + b = 0. This is also called the standard form.
Which equations are not linear equations in one variable? let’s understand with some examples.
1) x2 – 2 = 3
2) 3xy = 8
3) 7z + y = 18
4) 4x3 + 4 = 64
5) x + y + z = 0
All the above examples are not linear equations in one variable because either they have more than one variable or their value of the degree is more than 1.
What are the specific things and parts of the linear equations? let us understand with the help of an example.
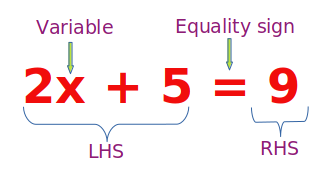
1) In the above equation, there is one and only one variable present which is x.
2) Because of the equality sign, this expression is called an equation.
3) All the numbers except the variable are called constants.
4) The expression written on the left side of the equality sign is called the Left Hand Side (LHS) and the expression written on the right side of the equality sign is called the Right Hand Side (RHS).
5) For certain values of the variable x, the values of the expression on the LHS and RHS are equal. These values are the solutions to the given equation.
How to Solve Linear Equations in One Variable?
The solution method of the linear equations in one variable is very simple and easy. When the variable is written on one side of the equality sign and numbers are written on the other side of the equality sign then how do we solve these types of linear equations? let’s see.
Example 1) Solve the equation 4x = 20.
Solution – 4x = 20
On transposing the number 4 to RHS
x = 20/4
x = 5 Ans.
Example 2) Find the solution of 3x + 2 = 23.
Solution – 3x + 2 = 23
On transposing the number 2 to RHS
3x = 23 – 2
3x = 21
On dividing both sides by 3
3x/3 = 21/3
x = 7 Ans.
Example 3) Solve 7x – 3 = -16.
Solution – 7x – 3 = -16
On adding 3 to both sides
7x – 3 + 3 = -16 + 3
7x = -13
On transposing 7 to RHS
x = -13/7 Ans.
Example 4) Solve 9/7 = 2/7 + y.
Solution – 9/7 = 2/7 + y
On transposing 2/7 to LHS
9/7 – 2/7 = y
Denominators are the same so we directly subtract numerators.
(9 – 2)/7 = y
7/7 = y
1 = y
or y = 1 Ans.
Example 5) Find the solution of 18 – 5z = -3
Solution – 18 – 5z = -3
On transposing 18 to RHS
-5z = -3 – 18
-5z = -21
On transposing -5 to RHS
z = -21 / -5
z = 21/5 Ans.
Note – When we perform any operation to solve the equation, we perform that operation on both sides (LHS and RHS) to balance the equation. Like adding a number to the equation, subtracting any number, multiplying, and dividing any number.