Introduction to Euclid’s Geometry Class 9th

1. Before knowing the introduction of Euclid’s geometry, we do know that the word ‘Geometry’ is a Greek word and is made of two words ‘geo’, meaning the ‘earth’, and ‘metrein’ meaning ‘to measure’.
2. Euclid the Egyptian mathematician, who was a teacher of mathematics at Alexandria in Egypt, discovered his famous treatise, called ‘Elements’.
3. ‘Elements’ was the collection of all the knowledge of mathematics known up to that time, arranged by Euclid.
4. ‘Elements’ was divided into thirteen chapters; each chapter is called a book.

Euclid’s Definitions, Axioms, and Postulates

Euclid listed 23 definitions in book 1 of the ‘Elements’. A few of them are given below :

1. A point is that which has no part.
2. A line is breadthless length.
3. The ends of a line are points.
4. A straight line is a line which lies evenly with the points on itself.
5. A surface is that which has length and breadth only.
6. The edges of a surface are lines.
7. A plane surface is a surface which lies evenly with the straight lines on itself.

Euclid gave some certain properties which were assumed by him and which were not proved. Actually, these assumptions were ‘obvious universal truths’. There were two types of these assumptions: axioms and postulates.

Axioms – Axioms were common notions and were assumptions used throughout mathematics and were not specifically linked to geometry.

Some of Euclid’s axioms are given below:

1. Things which are equal to the same thing are equal to one another.
2. If equals are added to equals, the wholes are equal.
3. If equals are subtracted from equals, the remainders are equal.
4. Things which coincide with one another are equal to one another.
5. The whole is greater than the part.
6. Things which are double of the same things are equal to one another.
7. Things which are halves of the same things are equal to one another.

The first axiom could be applied to plane figures. For example, if an area of a square equals the area of a rectangle and the area of the rectangle equals the area of a triangle, then the area of the square also equals the area of the triangle.

According to the 4^th axiom, if two figures are identical then they are equal. For example, if a triangle coincides with another triangle then both triangles are equal.

The 5^th axiom gives the definition of ‘greater than’. For example, if a square is part of a rectangle then the rectangle is greater than the square. Rectangle > square

Postulates – Postulates were the assumptions that were specifically linked to geometry.

Here, we will discuss Euclid’s five postulates.

Postulate 1 : A straight line may be drawn from any one point to any other point.

According to this postulate, a straight line passes through two different points, but we know that if there are two different points then only one straight line can be passed through them. Euclid did not mention that there cannot be more than one such line. There will be a unique line joining two different points. We can write this result in the form of an axiom as follows:

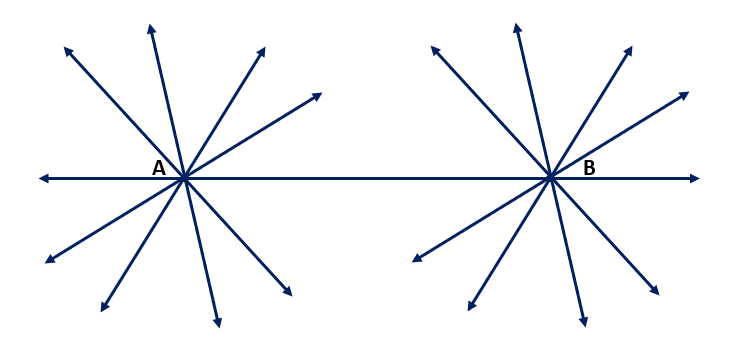
Axiom : There is a unique line that passes through two distinct points.

If we consider two points A and B, then how many lines passing through point A also pass through point B? We know that only one, and that is line AB. Similarly, how many lines passing through point B also pass through point A? Again, only one, and that is line AB. The figure shows it clearly.

Postulate 2 : A terminated line can be produced indefinitely.

Nowadays we use the term line segment, Euclid called it a terminated line. We know that a line segment can be extended in both directions to form a line. We can see this in the below figure.

Postulate 3 : A circle can be drawn with any centre and any radius.

We can draw a circle with any centre and of any radius.

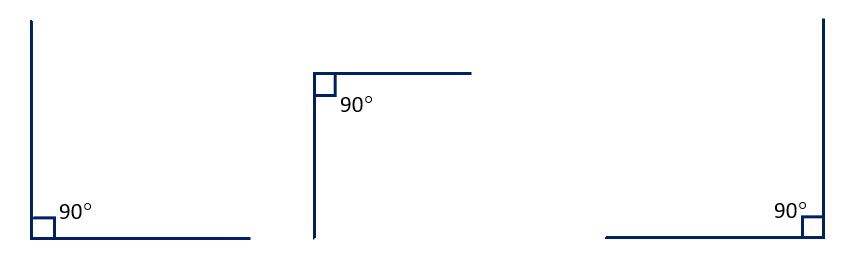
Postulate 4 : All right angles are equal to one another.

We know that the measure of the right angle is 90° so all right angles are equal.

Postulate 5 : If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.

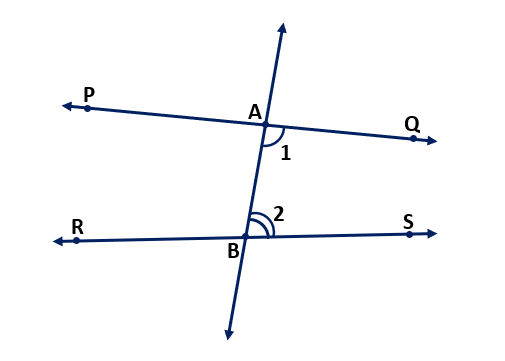
In the above figure, straight line AB falls on straight lines PQ and RS such that the sum of the interior angles 1 and 2 is less than 180° on the right side of line AB. It means lines PQ and RS will eventually intersect on the right side of AB.

Note – 1) Nowadays postulates and axioms are used in the same sense. Any statement is made on the basis of an observed phenomenon in the universe and its truth or validity is checked afterwards. If the statement is true, then it is accepted as a ‘Postulates’.

2) A system of axioms is called consistent. A consistent system is that in which any statement does not contradict any axiom or previously proved statement.

3) Euclid used his axioms and postulates to prove other results and using these results, he proved some more results by applying deductive reasoning. These proved statements are called propositions or theorems.

Examples of Euclid’s Axioms and Postulates

Example (1) If P, Q, and R are three points on a line, and Q lies between points P and R, then prove that PQ + QR = PR.

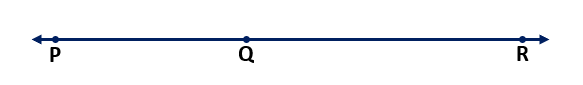
Solution – According to Euclid’s 4^th axiom, Things which coincide with one another are equal to one another.

Here, in the above figure, PR is coinciding with PQ + QR. So, it can be deduced that

PQ + QR = PR                   Hence proved.

Example (2) Prove that an equilateral triangle can be constructed on any given line segment.

Solution – Let AB be a line segment of any length.

Now, we do some construction. According to Euclid’s postulate 3, A circle can be drawn with any centre and any radius. We draw a circle with point A as the centre and AB as the radius. Similarly, we draw another circle with point B as the centre and BA as the radius.

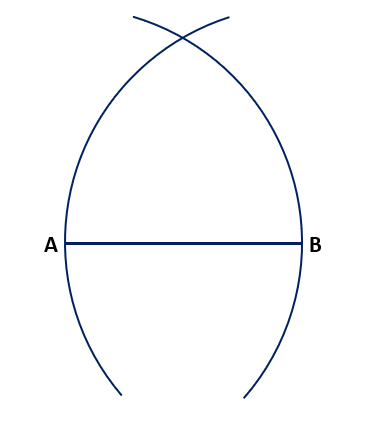
The two circles meet at a point, let the point be C. Now, we join points A and B to point C to form a triangle ABC.

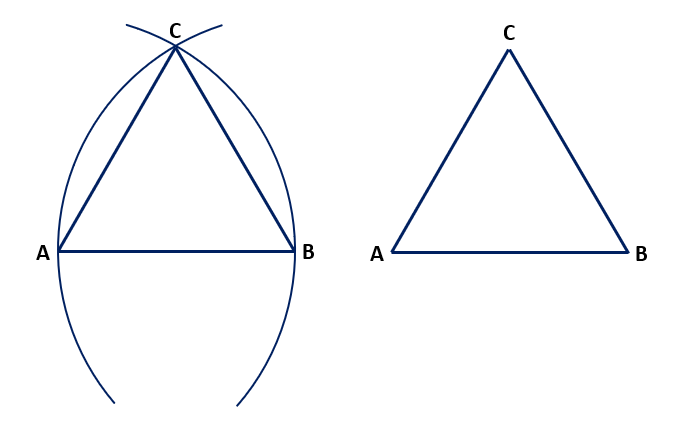
We have to prove that triangle ABC is an equilateral triangle, i.e., AB = BC = AC.

In the triangle ABC, AB = AC [radii of the same circle] ………… (1)

AB = BC [radii of the same circle] …………… (2)

Using Euclid’s axiom (1), Things which are equal to the same thing are equal to one another.

From equations (1) and (2), we can conclude that AB = BC = AC.

Therefore, triangle ABC is an equilateral triangle.              Hence proved.

Theorem : Two distinct lines cannot have more than one common point.

Proof – Let there be two distinct lines l and m. We have to prove that they have only one common point. For the common point, both lines must intersect each other.

Let us suppose that two lines intersect each other in two distinct points, say P and Q. It means there are two lines passing through two distinct points P and Q. But according to Euclid’s axiom that there is a unique line that can pass through two distinct points. So, our assumption that two lines can pass through two distinct points is wrong.

From the above explanation, we can conclude that two distinct lines cannot have more than one common point.                       Hence proved.

Equivalent Versions of Euclid’s Fifth Postulate

In Euclid’s fifth postulate, if the sum of the measures of the interior angles on the same side of the falling line is exactly 180°, then the lines will not intersect each other. In 1729, a Scottish mathematician John Playfair gives an axiom which is known as ‘Playfair’s axiom’.

He stated : ‘For every line l and for every point P not lying on l, there exists a unique line m passing through P and parallel to l’.

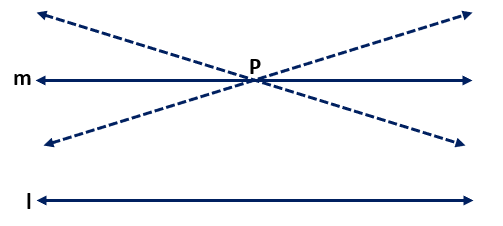
This result can also be stated in the following form :

Two distinct intersecting lines cannot be parallel to the same line.

Example – Consider the following statement : There exists a pair of straight lines that are everywhere equidistant from one another. Is this statement a direct consequence of Euclid’s fifth postulate? Explain.

Solution – Using Playfair’s axiom, let l be a line and P be a point that does not lie on l. Then there is a unique line m passing through point P which is parallel to line l.

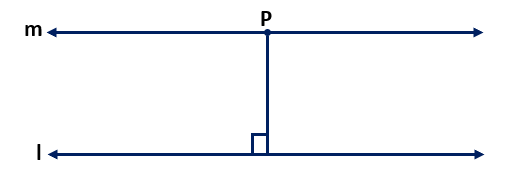
We know that distance of a point from a line is the length of the perpendicular from the point to the line. Similarly, the distance of any point on line m from line l and the distance of any point on line l from line m will be the same. Therefore, these two lines are everywhere equidistant from one another.                  Hence proved.

Introduction to Euclid’s Geometry Class 9th in Hindi

More About Euclid’s Geometry