Circles Passing Through Different Points Class 10th

Circles Passing Through Different Points are as follows.

Circles Passing Through One Point

If there is a point in a plane then through that point many circles can pass. We can say infinite circles can pass. We can understand it practically from the figure given below.

Circles Passing Through Two Points

If there are two points in a plane then also an infinite number of circles can pass through those two points. Here is the figure below to understand it clearly.

In the above figure, the Centre of all the circles lies on a straight line which is the perpendicular bisector of the line AB. Here, line AB is a chord.

Circles Passing Through Three Points

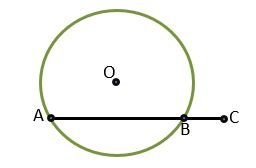
If there are three points and they lie on a straight line means they are collinear then we see that we can’t draw a circle that passes through all three points. In this condition, The second or third point will lie inside or outside the circle passing through two points.

Now, if we take three points that do not lie on a straight line means they are non-collinear. In this condition, only one circle can be drawn, and how, let’s see below. Let there be three points A, B, and C which are non-collinear as shown below.

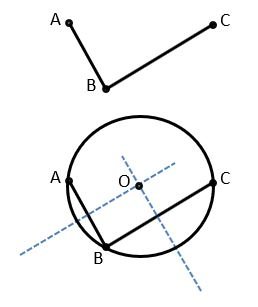
Joining the three points A, B, and C and after that, if we draw perpendicular bisectors of AB and BC then both the perpendicular bisectors intersect each other at a point. If we consider this point as a Centre O and OA as a radius and draw a circle then that circle will pass through all three points. It means OA = OB = OC

It shows that all three points are equidistant from point O and there is only one intersecting point of both the perpendicular bisector so, we can draw only one circle. Therefore, there is one and only one circle passing through three non-collinear points.

Circles Passing Through Different Points Class 10^th in Hindi

More About Circles Passing Through Different Points

Related posts

Area of Triangle in Coordinate Geometry Class 10th Tangent and Secant of Circle Class 10th About Libre office. Angle Subtended by the Arc of a Circle Class 10th Coordinate Geometry (Analytical Geometry) Class 10th Introduction to Euclid’s Geometry Class 9th Apache Open Office. Angle Subtended by a Chord of Circle Class 10th Areas Related to Circles Class 10th Lines and Angles Class 9th Trigonometry Class 10th Circles Class 10th Linear Equations in Two Variables Class 9th विभिन्न बिंदुओं से गुजरने वाले वृत्त कक्षा 10 (Circle Passing Through Different Points Class 10th) About Microsoft office 2016 Distance Between Two Points in Cartesian Plane and Distance Formula Class 10th Section Formula Class 10th About Microsoft Office 2013 Pro Plus. Coordinate Geometry Class 9th Angles of the Alternate Segment of a Circle Class 10th Representation of Real Numbers on the Number Line Class 9th वृत्त की स्पर्श रेखा और छेदक रेखा कक्षा 10 (Tangent and Secant of Circles Class 10th) Polynomials Class 10th Operations on Real Numbers Class 9th C language Algorithms, Flowchart, and Terms. Everything About Microsoft Windows 10. Circumference of Circle Class 10th Geometrical (Graphical) Meaning of the Zeroes of a Polynomial Class 10th बहुपद कक्षा 10 (Polynomial Class 10th) About Microsoft Office 2013 Pro Plus Hindi. Cyclic Quadrilaterals Class 10th Triangle and its Properties Class 10th About Microsoft office 2016 Hindi About Libre office In Hindi. त्रिकोणमिति कक्षा 10 (The Trigonometry Class 10th) Pair of Linear Equations in Two Variables Class 10th वृत्त की जीवा द्वारा अंतरित कोण कक्षा 10 (Angle Made by a Chord of Circle Class 10th) Pythagoras Theorem (Boudhayana Theorem) Class 10th Mensuration Q & A Trigonometric Ratios of Acute Angles Class 10th रेखाएँ और कोण कक्षा 9 (Lines and Angles Class 9th) Learn Java Script Programming वृत्तों से संबंधित क्षेत्रफल कक्षा 10 (Areas Related to Circle Class 10th) Apache Open Office Hindi. Arithmetic Progression Class 10th About Assembly Programming What is Nodejs Everything About Microsoft Windows 10 Hindi. निर्देशांक ज्यामिति कक्षा 10 (The Coordinate Geometry Class 10th) About Objective C Programming About Vue.js The Similarity of Triangles Class 10th What Is Bootstrap Css एक वृत्त के चाप द्वारा अंतरित कोण कक्षा 10 (Angles Made by the Arc of Circle Class 10th) About Python Tableau Heron’s Formula Class 9th What Is Tailwind Css Microsoft Windows Legacy Operating system. Surface Areas and Volumes Class 10th Polynomials Class 9th Decimal Expansion of Rational Numbers Class 10th Learn Html5 Learn C Programming एक वृत्त के एकान्तर खंड के कोण कक्षा 10 (Angles of Alternate Segment of Circle Class 10th) वृत्त और इसके भाग कक्षा 10 (Circle and its Parts Class 10th) About Scala Programming Decimal Expansions of Real Numbers Class 9th About Wps Office. Number System Class 9th Whole Numbers Class 6th Perimeter and Area Class 6th समान्तर श्रेढ़ी कक्षा 10 (Arithmetic Progressions Class 10th) Trigonometric Ratios of Some Specific Angles Class 10th About Raspberry pi board Quadratic Equation Class 10th What Is Bulma Css Learn Html About mysql About ReactJs Framework त्रिभुज और इसके गुण कक्षा 10 (The Triangle and its Properties Class 10th) About Scipy Python Library About Kotlin Programming About Arduino Microcontroller Board About Microsoft Windows 7. द्विघात समीकरण कक्षा 10 (Quadratic Equations Class 10th) About Xml Sets Class 11th Decimal Numbers Class 7th बहुपद के शून्यकों का ज्यामितीय (आलेखीय) अर्थ कक्षा 10 [Geometrical (Graphical) Meaning of the Zeroes of the Polynomial Class 10th] What Is The Internet? About MongoDb Database Integers Class 6th Sum of First n Terms of an Arithmetic Progression Class 10th Microsoft Windows 10 Operating System Apps. Learn Java Programming वृत्त की परिधि कक्षा 10 (The Circumference of Circle Class 10th) Pc assembly and its operation. हीरोन का सूत्र कक्षा 9 (Heron’s Formula Class 9th) About Pandas Irrational Numbers and Irrationality Class 10th About Postgresql nth Term (General Term) of an Arithmetic Progression Class 10th वास्तविक संख्याओं पर संक्रियाएँ कक्षा 9वीं (Operations on Real Numbers Class 9th) समान्तर श्रेढ़ी के पहले n पदों का योग कक्षा 10 (Sum of n Terms of Arithmetic Progression Class 10th) About Pl/Sql About Microsoft Windows 7 Hindi. About Microsoft office 365. परिमाप और क्षेत्रफल कक्षा 6 (Perimeter and Area for Class 6th) About Json json javascript object notation यूक्लिड की ज्यामिति का परिचय कक्षा 9 (Introduction to Euclid’s Geometry Class 9th) About Python Numpy Rational Numbers Class 8th Linux, What is Linux, A Complete Overview of Ubuntu Linux. Types of Network Communication Media And Network Topology. संख्या रेखा पर वास्तविक संख्याओं का निरूपण कक्षा 9वीं (Representation of Real Numbers on the Number Line Class 9th) About Magento Programming विभाजन सूत्र कक्षा 10 (The Section Formula Class 10th) About Perl Programming कुछ विशिष्ट कोणों के लिए त्रिकोणमितीय अनुपात कक्षा 10 (Trigonometric Ratios of Specific Angles Class 10th) समुच्चय कक्षा 11 (The Sets Class 11th) What Is Express.js Some Applications of Trigonometry Class 10th Microsoft Windows 10 Apps Hindi. समान्तर श्रेढ़ी का n वाँ पद (व्यापक पद) कक्षा 10 (nth Term of Arithmetic Progression Class 10th) HTML Elements Operations on Polynomials Class 10th Microsoft Windows 8 Apps. चक्रीय चतुर्भुज कक्षा 10 (Cyclic Quadrilateral Class 10th) पाइथागोरस प्रमेय (बौधायन प्रमेय) कक्षा 10 (The Pythagoras Theorem Class 10th) Microsoft Windows Legacy Operating System Hindi. About C# Programming Internet Technology And Network Protocols. निर्देशांक ज्यामिति कक्षा 9 (The Coordinate Geometry Class 9th) Type of Computer Programming. About Go Programming Language दो चर वाले रैखिक समीकरण युग्म कक्षा 10 (Pair of Linear Equations in Two Variables Class 10th) दशमलव संख्याएँ कक्षा 7 (Decimal Number Class 7th) About Typescript Language What Is A Search Engine and Their Type? Relation Between Trigonometric Ratios Class 10th कार्तीय समतल में दो बिन्दुओं के बीच की दूरी और दूरी सूत्र कक्षा 10 (The Distance Formula Class 10th) बहुपदों पर संक्रियाएँ कक्षा 10 (Operation on Polynomial Class 10th) Microsoft Windows 8 Apps Hindi. Input And Output Device. About Joomla Cms Computer Fundamental. What Is Jquery/javascript query An In-Depth Review of imagestotext.io in 2023 पूर्णांक संख्याएँ कक्षा 6 (Integer Class 6th) Computer Motherboard and its Components.