nth Term (General Term) of an Arithmetic Progression Class 10th

Derivation

To find the nth term (general term) of an Arithmetic Progression, First of all, We know the general form of an Arithmetic Progression which is given as

a, a + d, a + 2d, a + 3d, a + 4d,……………..a + (n – 1)d

Here, we can see that the first term is a.

To find the second term we are adding common difference d to the first term a or we can say that we are multiplying common difference (d) with (2 – 1) and then adding it to the first term a.

a₂ = a + d = a + (2 – 1)d

To find the third term, same as above we are multiplying d with (3 – 1) and add to the first term a.

a₃ = a + 2d = a + (3 – 1)d

Similarly, to find the nth term (general term) of an Arithmetic Progression we will multiply d with (n – 1) and then add to the first term as written in general form also.

a_n = a + (n – 1)d

Here, a_n = n^th term or general term

a = First term

n = Number of terms

d = Common difference

If there are finite terms in an AP then a_n represents the last term which is also denoted by l.

Some Examples

Example 1) find the 9^th term of the AP 6, 12, 18, 24, 30…………..

Solution – Here first term (a) = 6, common difference (d) = 12 – 6 = 6

The number of terms (n) = 9,     9th term (a₉) =?

By the formula of n^th term,   a_n = a + (n – 1)d

a₉ = 6 + (9 – 1)6

a₉ = 6 + (8)6 = 6 + 48

a₉ = 54

So, the 9^th term of the given AP is 54.            Ans.

Example 2) Which term of an AP 4, 8, 12, 16……….. is 464?  

Solution – First term (a) = 4, common difference (d) = 8 – 4 = 4

n^th term (a_n) = 464, Number of term (n) = ?

By the formula,    a_n = a + (n – 1)d

464 = 4 + (n – 1)4

464 – 4 = 4n – 4

460 = 4n – 4

460 + 4 = 4n

464 = 4n

464/4 = n

n = 116

Therefore, the 116^th term of the given AP is 464.              Ans.

Example 3) Find the n^th term (general term) of AP 7, 11, 15, 19……..

Solution – First term (a) = 7, common difference (d) = 11 – 7 = 4

n^th term (a_n) =?

By the formula of n^th term,   a_n = a + (n – 1)d

a_n = 7 + (n – 1)4

a­_n = 7 + 4n – 4

a_n = 3 + 4n

So, the n^th term of the AP is a_n = 3 + 4n             Ans.

Example 4) Find the number of terms of AP 1, 8, 15, 22……………..,204.

Solution – Here First term (a) = 1, common difference (d) = 8 – 1 = 7

n^th term (a_n) = 204, Number of terms (n) = ?

By formula,    a_n = a + (n – 1)d

204 = 1 + (n – 1)7

204 – 1 = 7n – 7

203 = 7n – 7

203 + 7 = 7n

210/7 = n

n = 30

So, there are 30 terms in the given AP.               Ans.

Example 5) For AP 10, 7, 4, 1, -2, -5, -8, -11….check whether -31 is the term of it or not.

Solution – First term (a) = 10, common difference (d) = 7 – 10 = -3

If -31 is the term of the given AP then the number of terms(n) for it will be a natural number.

So, the nth term (a_n) = -31 then the number of terms (n) =?

n^th term formula,     a_n = a + (n – 1)d

-31 = 10 + (n – 1)(-3)

-31 – 10 = -3n + 3

-41 = -3n + 3

3n = 41 + 3

n = 44/3 = 14.67

Since the value of n is the decimal number. n is always a natural number for AP.

Therefore, -31 is not the term of the given AP.              Ans.

Example 6) Determine the AP whose 5^th term is 9 and 9^th term is 17.

Solution – By the formula of n^th term,       a_n = a + (n – 1)d

5^th term a₅ = a + (5 – 1)d               9^th term a₉ = a + (9 – 1)d

9 = a + 4d                                       17 = a + 8d

Solving both the equation,

a + 4d = 9 ……………..(1)                              a + 8d = 17 ………………(2)

By substitution method,                                        

a + 4d = 9                                                   9 – 4d + 8d = 17

a = 9 – 4d[putting the value in equation (2)]      4d = 17 – 9

a = 9 – 4d ……………..(3)                                    d = 8/4     

a = 9 – 4⨯2                          d = 2 (Common difference)[putting the value in equation (3)]         

a = 9 – 8

a = 1 (First term)

So, the required AP is 1, 3, 5, 7, 9, 11, 13, 15, 17, 19………..               Ans.

Example 7) If the 6th term of an AP is 22 and the 30^th term is 94. Find its 25^th term.

Solution – By n^th term formula,    a_n = a + (n – 1)d

6^th term,  a₆ = 22              30^th term,   a₃₀ = 94

a + (6 – 1)d = 22                a + (30 – 1)d = 94

a + 5d = 22                          a + 29d = 94

Solving by elimination method,

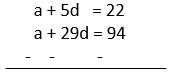
-24d = – 72

d = -72/-24

Common difference   d = 3  

Putting the value d = 3 in any equation,

a + 5d   = 22     

a + 5⨯3 = 22

a = 22 – 15

First term    a = 7

Now 25^th term,     a₂₅ = a + (25 – 1)d

a₂₅ = 7 + 24⨯3

a₂₅ = 7 + 72

a₂₅ = 79

Hence the 25^th term of the given AP is 79.              Ans.

Example 8) How many two digits numbers are divisible by 9?

Solution – Two digits numbers = 10 to 99

Numbers which are divisible by 9, 18, 27, 36…………………..99

This sequence will be AP because all numbers are divisible by 9.

First-term (a) = 18, common difference (d) = 27 – 18 = 9

n^th term (a_n) = 99, number of terms (n) = ?

By the formula,     a_n = a + (n – 1)d

99 = 18 + (n – 1)9

99 – 18 = 9n – 9

81 + 9 = 9n

90 = 9n

n = 90/9 

n = 10

So, there are 10 two digits numbers divisible by 9.              Ans.

n^th Term From the Last Term

If we take the last term ‘l ’ as the first term and reverse the common difference as – d then the n^th term from last can be written as follows

n^th term from last    a_n =  l + (n – 1)(-d)

a_n = l – (n – 1)d

Example 9) Find the 16^th term from the last term of the AP 21, 18, 15, 12…………….-81.

Solution – Here last term ( l ) = -81, common difference (d) = 18 – 21 = -3, number of terms (n) = 16

By the formula of the nth term from the last term,     a_n = l – (n – 1)d

a₁₆ = -81 – (16 – 1)(-3)

a₁₆ = -81 – (-48 + 3)

a₁₆ = -81 – (-45)

a₁₆ = -81 + 45

a₁₆ = – 36

So, the 16^th term from the last term is -36.              Ans.

How to Select Terms of Arithmetic Progression if not Given –

If there is a question in which neither AP is given nor any term is given and we have to find the AP then we have to select the terms of AP in a different order. Selection of the terms of AP in different order helps us to find the AP easily. Let’s see how to select the terms.

If we have to select three terms then the terms are –  a – d, a, a + d

If we have to select four terms then the terms are –  a – 3d, a – d, a + d, a + 3d

If we have to select five terms then the terms are –  a – 2d, a – d, a, a + d, a + 2d

If we have to select six terms then the terms are –  a – 5d, a – 3d, a – d, a + d, a + 3d, a + 5d  

Example 10) Three numbers are in AP if their sum is 15 and the product is -55 then find the numbers.

Solution – Let the three numbers which are in AP   a – d, a, a + d

Then, according to the question, the sum is 15 so,  a – d + a + a + d = 15

3a = 15

a = 15/3

a = 5

And the product is -55       (a – d)⨯a⨯(a + d) = -55

(a² – d²)⨯a = -55

∵ a = 5

{(5)² – d²}⨯5 = -55

{25 – d²}⨯5 = -55

25 – 5d² = -55 

125 + 55 = 5d²

180 = 5d²

180/5 = d²

d² = 36

d = ±√36

d = ±6

Putting the value of a and d. if a = 5 and d = +6 then numbers 5 – 6, 5, 5 + 6 ⇒ -1, 5, 11

If a = 5 and d = -6 then numbers 5 – (-6), 5, 5 + (-6) ⇒ 11, 5, -1              Ans.

nth Term (General Term) of an Arithmetic Progression Class 10^th in Hindi

More About n^th Term (General Term) of an Arithmetic Progression