Whole Numbers Class 6th

Introduction

We know that counting numbers begin with 1, 2, 3, 4, 5……… these numbers are called natural numbers. It means all the counting numbers are called Natural numbers. Natural numbers come under the whole numbers. In class 6^th, whole numbers are as follows.

Definition

All the counting numbers including zero (0) are called Whole Numbers or Natural numbers along with zero (0) are called Whole Numbers. It is denoted by W.

Example – W = {0, 1, 2, 3, 4, 5, 6, 7……….}

Whole numbers do not include fractions and decimal numbers like 2/3, ½, 3.4, 5.6, etc.

Important Points

• Whole numbers are Real numbers.
• All the natural numbers are whole numbers.
• All the positive integers including zero (0) are whole numbers.
• 0 is the smallest whole number.

Predecessor and Successor of Whole Numbers

Predecessor – if we subtract 1 from any number, we get the predecessor of that number. For whole numbers, every number other than 0 has its predecessor.

Examples – predecessor of 2 = 2 – 1 = 1

Predecessor of 11 = 11 – 1 = 10

Predecessor of 100 = 100 – 1 = 99

Predecessor of 0 = 0 – 1 = -1 (not a whole number)

Successor – if we add 1 to any number, we get the successor of that number. For whole numbers, every number has its successor.

Examples – successor of 0 = 0 + 1 = 1

Successor of 56 = 56 + 1 = 57

Successor of 4 = 4 + 1 = 5

Successor of 999 = 999 + 1 = 1000

Whole Numbers on The Number Line

we draw a line and mark the whole numbers 0, 1, 2, 3…. on it at equal distances. That line is the number line for whole numbers.

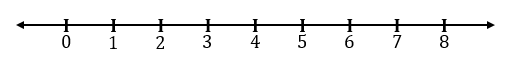
The equal distance between the numbers is called the unit distance. On the right side of the number line, the whole numbers increase.

On the number line, the distance between whole numbers 0 and 1 = 1 unit

Distance between whole numbers 1 and 3 = 2 unit

Addition of The Whole Numbers on The Number Line

If we add two whole numbers then the result will be on the right side of both the numbers on the number line. Let’s add 2 and 5.

For the addition of 2 and 5, we start from 2 and take 5 jumps to the right side as shown in the above figure. Each jump is equal to 1 unit. The tip of the 5^th arrow is at the number 7. Therefore, the sum of 2 and 5 is 7.

2 + 5 = 7

Subtraction of The Whole Numbers on The Number Line

In the subtraction of two numbers, we get the result by jumping on the left side of the number line. Let’s take an example. Subtract 3 from 5.

For the subtraction of 3 from 5, we start from 5 and take 3 jumps to the left side as shown in the figure. The tip of the 3^rd arrow is at 2. Therefore, the subtraction of 3 from 5 is equal to 2.

5 – 3 = 2

Multiplication of The Whole Numbers on The Number Line

In multiplication, we get the result by jumping on the right side of the number line. But the jump is not equal to 1 unit, it depends on the numbers, which are to be multiplied. Let’s multiply 4×2.

We start from 0 and jump 2 units at a time to the right side. We take such 4 moves. After taking such 4 moves, the tip of the last arrow is at 8. Therefore, the result is 8.

4 × 2 = 8

Properties of The Whole Numbers

(1) Closure Property

For addition – the sum of two whole numbers is always a whole number. This property is known as closure property for addition.

Examples – 1) 2 + 3 = 5 (whole number)

2) 4 + 7 = 11 (whole number)

3) 1 + 9 = 10 (whole number)

For subtraction – the difference of two whole numbers is not always a whole number. It means whole numbers are not closed under subtraction.

Examples – 1) 5 – 4 = 1 (whole number)

2) 6 – 8 = -2 (not a whole number)

3) 1 – 9 = -8 (not a whole number)

For multiplication – the multiplication of two whole numbers is always a whole number. This property is the closure property for multiplication.

Examples – 1) 3 × 7 = 21 (whole number)

2) 4 × 1 = 4 (whole number)

3) 6 × 3 = 18 (whole number)

For division – the division of two whole numbers is not always a whole number. It means whole numbers are not closed under division.

Examples – 1) 9 ÷ 3 = 3 (whole number)

2) 5 ÷ 8 = 5/8 (not a whole number)

3) 1 ÷ 0 = ∞ (infinitive)

(2) Commutative Property

For addition – the sum of two whole numbers in any order is always the same whole number. This is the commutativity property for addition.

Examples – 1) 4 + 5 = 5 + 4 = 9 (same whole number)

2) 8 + 6 = 6 + 8 = 14 (same whole number)

For subtraction – the subtraction of two whole numbers in any order is not always the whole number. It means the subtraction is not commutative for whole numbers.

Examples – 1) 8 – 3 = 5 (whole number) and 3 – 8 = -5 (not a whole number)

2) 5 – 1 = 4 (whole number) and 1 – 5 = -4 (not a whole number)

For multiplication – the multiplication of two whole numbers in any order is always the same whole number. This is the commutativity property for multiplication.

Examples – 1) 3 × 5 = 5 × 3 = 15 (same whole number)

2) 8 × 9 = 9 × 8 = 72 (same whole number)

For division – the division of two whole numbers in any order is not always the whole number. It means whole numbers are not commutative for division.

Examples – 1) 4 ÷ 2 = 2 (whole number) and 2 ÷ 4 = ½ (not a whole number)

2) 9 ÷ 3 = 3 (whole number) and 3 ÷ 9 = 1/3 (not a whole number)

(3) Associative Property

For addition – if a, b, and c are three whole numbers then the associativity of addition will be

(a + b) + c = a + (b + c)

Example – (2 + 3) + 5 = 2 + (3 + 5)

5 + 5 = 2 + 8

10 = 10

For subtraction – whole numbers are not associative for subtraction.

(a – b) – c ≠ a – (b – c)

Example – (2 – 3) – 5 ≠ 2 – (3 – 5)

-1 – 5 ≠ 2 – (-2)

-6 ≠ 2 + 2

-6 ≠ 4

For multiplication – if a, b, and c are three whole numbers then the associativity of multiplication will be

(a × b) × c = a × (b × c)

Example – (2 × 3) × 5 = 2 × (3 × 5)

6 × 5 = 2 × 15

30 = 30

For division – whole numbers are not associative for division.

(a ÷ b) ÷ c ≠ a ÷ (b ÷ c)

Example – (2 ÷ 3) ÷ 5 ≠ 2 ÷ (3 ÷ 5)

2/3 ÷ 5 ≠ 2 ÷ 3/5

2/3 × 1/5 ≠ 2 × 5/3

2/15 ≠ 10/3

(4) Distributive Property of Multiplication Over Addition

if a, b, and c are three whole numbers then

a × (b + c) = (a × b) + (a × c)

Example – 2 × (3 + 5) = (2 × 3) + (2 × 5)

2 × 8 = 6 + 10

16 = 16

This is known as the distributivity of multiplication over addition.

(5) Identity Property

For addition – when zero (0) is added to any whole number then the result is always the whole number itself. Zero (0) is called the additive identity for whole numbers.

Examples – 1) 0 + 4 = 4

2) 7 + 0 = 7

For multiplication – when 1 is multiplied by any whole number then the result is always the whole number itself. 1 is called the multiplicative identity for whole numbers.

Examples – 1) 1 × 8 = 8

2) 3 × 1 = 3

Note – Identity property cannot be used for subtraction and division.

Whole Numbers Class 6^th in Hindi

More About Whole Numbers