Cyclic Quadrilaterals Class 10th

Introduction

Definition – The quadrilaterals whose all four vertices lie on the circle are called Cyclic Quadrilaterals.

Here, ABCD is a cyclic quadrilateral. Its vertices A, B, C and D are situated on the circle.

If we measure all four angles and add the opposite angles then we will find that sum of opposite angles is 180°. It means opposite angles are supplementary.

We can prove it with self-activity and with the help of the theorem.

Theorems Based on it

Theorem 1) The opposite angles of a cyclic quadrilateral are supplementary (180°).

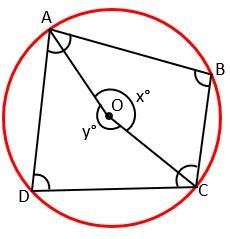
Given – ABCD is a cyclic quadrilateral.

Prove that – ∠A + ∠C = 180° and ∠B + ∠D = 180°

Construction – Joined points A and C to Centre O.

Proof – By arc ADC, the angle made on the Centre of the circle is y° and the angle made on the remaining part of the circle is ∠B. So, by theorem,

∠B = ½y° —————(1)

Similarly, by arc ABC, the angle made on the Centre of the circle is x° and the angle made on the remaining part of the circle is ∠D. So, by theorem,

∠D = ½x° —————(2)

Adding equations (1) and (2),

∠B + ∠D = ½y° + ½x° = ½(y° + x°)

∠B + ∠D = ½(360°)      [Angle made around the Centre of circle is y° + x° = 360°]

∠B + ∠D = 180° —————(3)

We know that the sum of four angles of a quadrilateral is 360°

So,   ∠A + ∠B + ∠C + ∠D = 360°

∠A + ∠C + 180° = 360°     [from equation (3), ∠B + ∠D = 180°]

∠A + ∠C = 360° – 180°

∠A + ∠C = 180° ——————(4)

From equations (3) and (4), it is proved that opposite angles of a cyclic quadrilateral are supplementary.    Hence Proved.

Converse of Theorem

Theorem 2) If opposite angles of a Quadrilateral are supplementary (180°), then it is a cyclic quadrilateral.

Given – PQRS is a quadrilateral in which

∠PQR + ∠PSR = 180°

∠QPS + ∠QRS = 180°

Prove that – PQRS is a cyclic quadrilateral.

Proof – Let a circle passes through points P, Q, R and S`. if we join PS` it becomes cyclic Quadrilateral PQRS`.

Then,  ∠PQR + ∠PS`R = 180° [sum of opposite angles of a cyclic quadrilateral]  ——————(1)

But     ∠PQR + ∠PSR = 180° [given] —————(2)

From equations (1) and (2)

∠PQR + ∠PS`R = ∠PQR + ∠PSR

∠PS`R = ∠PSR —————–(3)

But in △PSS`, ∠PS`R is an exterior angle so by exterior angle property,

∠PS`R = ∠PSS` + ∠SPS`

Therefore, ∠PS`R > ∠PSR —————(4)

From equations (3) and (4), it is clear that PS and PS` or point S and S` coincide with each other.

It proves that PQRS is a cyclic quadrilateral.           Hence Proved.

Relation Between Exterior Angle and Interior Opposite Angles of a Cyclic Quadrilateral –

In a cyclic quadrilateral, an Exterior angle is an angle made by increasing any side from any vertex. In the above figure, ∠CBE is an exterior angle made by increasing the side AB from vertex B.

Here, ∠ADC is a corresponding interior opposite angle of exterior angle ∠CBE.

If we measure ∠ADC then we shall find that the angle is equal to the exterior angle ∠CBE. We can understand it with the help of the theorem also.

Theorem 3) Exterior angle of a cyclic quadrilateral is equal to its corresponding interior opposite angle.

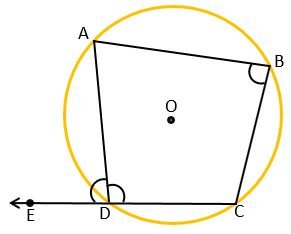
Given – ABCD is a cyclic quadrilateral in which ∠ADE is an exterior angle.

Prove that – ∠ABC = ∠ADE

Proof – ∵ ABCD is a cyclic quadrilateral. 

∴ Opposite angles will be supplementary.

∠ABC + ∠ADC = 180° ————(1)

∠ADE + ∠ADC = 180° [by linear pair angles] ————(2)

From equations (1) and (2),

∠ABC + ∠ADC = ∠ADE + ∠ADC

∠ABC = ∠ADE                 Hence Proved.

Converse of Theorem

Theorem 4) In a quadrilateral, if the exterior angle made by increasing a side is equal to an interior opposite angle, then it is a cyclic quadrilateral.

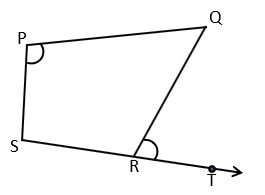
Given – PQRS is a quadrilateral in which ∠QPS = ∠QRT.

Prove that – PQRS is a cyclic quadrilateral.

Proof –  ∠QPS = ∠QRT [given]

Adding ∠QRS on both sides

∠QPS + ∠QRS  = ∠QRT + ∠QRS

∠QPS + ∠QRS = 180°   [by linear pair of angles ∠QRT + ∠QRS = 180°]

We know that ∠QPS and ∠QRS are opposite angles of quadrilateral PQRS and the sum of both is 180°. We know that opposite angles of the cyclic quadrilateral are supplementary.

So, it is proved that PQRS is a cyclic quadrilateral.        Hence Proved.

Examples –

Example 1) In the given figure If ∠POR = 146° then find the value of ∠PQR.

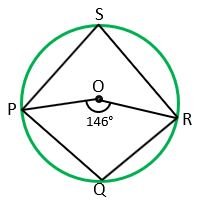
Solution – Here, by arc PQR angle made on the Centre, is ∠POR and the angle made on the remaining part of the circle is ∠PSR. So, by theorem,

∠PSR = ½∠POR

∠PSR = ½⨯(146°)

∠PSR = 73°

∵ PQRS is a cyclic quadrilateral.

∴ Opposite angles will be supplementary.

So, ∠PSR + ∠PQR = 180°

73° + ∠PQR = 180°

∠PQR = 180° – 73°

∠PQR = 107°         Ans.

Example 2) In the given figure, ABCD is a cyclic quadrilateral. The Angle subtended at the Centre of the circle by an arc ABC is 160°. Find ∠ADC and ∠CBE.

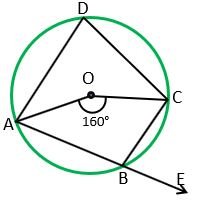
Solution – We know that the angle subtended by an arc at the Centre is two times the angle subtended at the remaining part of the circle.

∴ ∠ADC = ½∠AOC = ½⨯(160°)

∠ADC = 80°

In a cyclic quadrilateral, the exterior angle is equal to the interior opposite angle.

Therefore, ∠CBE = ∠ADC

∠CBE = 80°           Ans.

Cyclic Quadrilaterals Class 10^th in Hindi

More About Cyclic Quadrilaterals