Introduction
Definition – A set of points located at a fixed distance from a fixed point in a plane is called a Circle. The fixed point is called the centre and the fixed distance is called the radius of the circle. Examples – The path of the tip of the second’s hand in the clock, The figure is drawn around the coin of Rs 1, Rs 2, Rs 5, bangles, wheels, clocks, etc. are circles.
Circle and its Parts
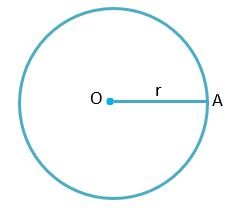
We draw the above circle with the help of a pencil and compass where point O is a fixed point and the distance OA is a fixed distance.
Centre (O) – The fixed-point O is called the Centre of the circle. On point O we put one leg (pointed leg) of the compass.
Radius (r) – The fixed distance OA is called the radius of the circle. Equal to the radius and with the help of another leg (in which we keep the pencil) of the compass a circle is drawn.
A circle divides the plane into three parts on which it lies –
1) Interior part (inside the circle)
2) The circle
3) Exterior part (outside the circle)

Note – The circle and the interior part together form the circular region.
Chord – The line segment which joins the two points situated on the circle is called a Chord. If we take two points A and B which are situated on the circle then line segment AB will be a chord of the circle.

There can be many chords in a circle.
Diameter (D) – The diameter is also a chord itself that passes through the Centre. So we can say that the chord which passes through the Centre of the circle is called the Diameter.

The diameter is the longest chord of the circle and all the diameters of the same circle have the same length. A circle has infinite diameters.
Note – There is a relation between radius and diameter. The diameter is double the radius or we can say that radius is half of the diameter.
So, we can write D = 2r
Or r = D/2
Arc – If we take two points on a circle then the circular length of that two points is called the Arc. One circular length is longer and another is smaller.
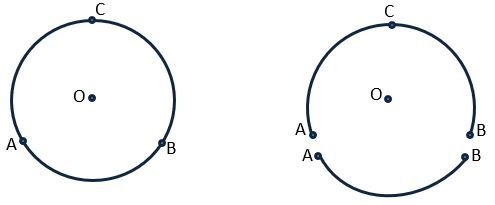
The smaller circular length is called minor arc AB and denoted by ![]() and the longer circular length is called major arc AB and denoted by
and the longer circular length is called major arc AB and denoted by ![]() . Point C is between the major arc AB to show the difference between the minor arc and the major arc.
. Point C is between the major arc AB to show the difference between the minor arc and the major arc.
Semicircle – When points A and B are at both ends of the diameter then in this condition both the major and minor arc will be equal and each arc is called a Semicircle.
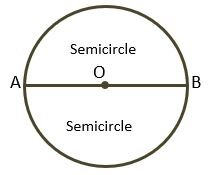
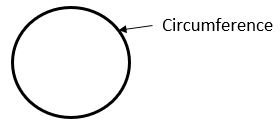
Circumference – The complete circular length of the circle is called the Circumference.
The Segment of the Circle – The region made by a chord and its corresponding arc is called the segment of the circle. There are two types of segments one is the minor segment and the other is the major segment.
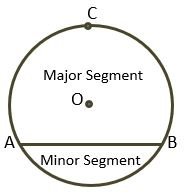
In the above figure, the region made by chord AB and minor arc AB is called a minor segment, and the region made by chord AB and major arc ACB is called a major segment.
The Sector of the Circle – The region made by an arc and two radii that are joining the Centre to the endpoints of the arc is called the sector of the circle.
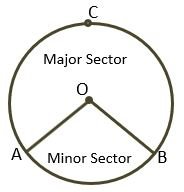
In the above figure, region OAB is a minor sector made by a minor arc, and region OACB is a major sector made by the major arc.