Trigonometry Class 10th

Introduction

Trigonometry is a very important and interesting branch of mathematics. The word ‘trigonometry’ is derived from the Greek words ‘tri’ (means three), ‘gon’ (means sides), and ‘metron’ (means measure). It is also said that this word is taken from the Sanskrit language word ‘त्रिकोणमिति’.Trigonometry is the study of relationships between the sides and the angles of a Right-angled triangle. In trigonometry, the right-angled triangle is used to find the sides and angles.

Trigonometric Functions

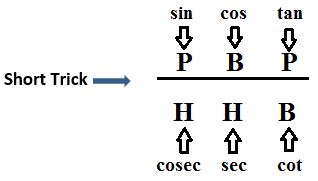
Generally, there are six trigonometric functions. They are sine, cosine, tangent, cosecant, secant, and cotangent. sine, cosine, and tangent are the main trigonometric functions, and cosecant, secant, and cotangent are reciprocal of these main functions respectively.

These trigonometric functions are used with angles in the right-angled triangle so they are used like this

sin ϴ, cos ϴ, tan ϴ, cosec ϴ, sec ϴ and cot ϴ

Trigonometric Ratios of an Acute Angle

In a right-angled triangle, the ratio of any two sides is known as the trigonometrical ratio. Each trigonometric function has a different ratio.

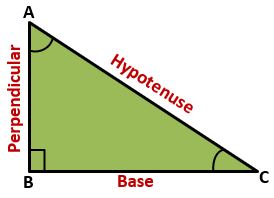
Base (BC) – Adjacent side of ∠C

Perpendicular (AB) – opposite side of ∠C

Hypotenuse (AC) – opposite side of ∠B (right angle)

In the above right-angled triangle, ∠B is a right angle and there are two acute angles ∠A and ∠C. for both acute angles trigonometric ratios can be found.

Trigonometric Ratios of Acute Angle ∠C

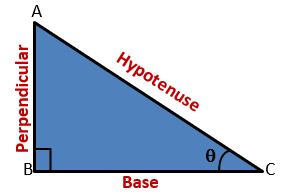
Let ∠C = ϴ

1) sin ϴ = Perpendicular/Hypotenuse = AB/AC  

2) cos ϴ = Base/Hypotenuse = BC/AC  

3) tan ϴ = Perpendicular/Base = AB/BC                          

4) cosec ϴ = Hypotenuse/Perpendicular = AC/AB  

5) sec ϴ = Hypotenuse/Base = AC/BC  

6) cot ϴ = Base/Perpendicular = BC/AB

We can also find all the trigonometric ratios for the acute angle A. for acute angle A Base (Adjacent side of ∠A) will be AB and the Perpendicular (opposite side of ∠A) will be BC. hypotenuse will remain the same (AC).

Note – 1)Trigonometric ratios depend on the acute angle ϴ not on the size of the Right-angled triangle.

2) The trigonometric ratios are unique for each acute angle ϴ.

3) sin ϴ ≠ sin⨯ϴ , cos ϴ ≠ cos⨯ϴ, tan ϴ ≠ tan⨯ϴ

It is not multiplication between trigonometric function and acute angle.

4) Trigonometric ratios of any positive acute angle are always positive.

Example – 1) In △ABC, ∠C is a right angle. side AB = 5 cm and BC = 4 cm then find all trigonometric ratios of angle A.

Solution –

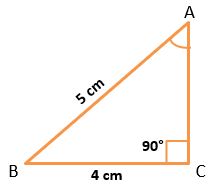
∵ △ABC is a right-angled triangle.

By Pythagoras theorem,

AC² = AB² – BC²

AC = √(5)² – (4)²

AC = √(25-16) = √9 = 3 cm

Now,

sin A = BC/AB = 4/5	cosec A = AB/BC = 5/4 (Reciprocal of sin A)
cos A = AC/AB = 3/5	sec A = AB/AC = 5/3 (Reciprocal of cos A)
tan A = BC/AC = 4/3	cot A = AC/BC = 3/4 (Reciprocal of tan A)

Example – 2) if sin ϴ = 24/25, then find the remaining trigonometric ratios of ϴ.

Solution – sin ϴ = 24/25 = Perpendicular/Hypotenuse

If we draw △ABC for sin ϴ = 24/25

Perpendicular = AB           and            Hypotenuse = AC

Let AB = 24k, AC = 25k

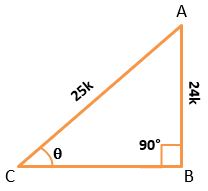
Where k = proportionality constant

In △ABC By Pythagoras theorem,

BC = √(AC)² – (AB)²                 

BC = √(25k)² – (24k)²                              

BC = √625k² – 576k²                      

BC = √49k² 

BC = ±7k

since angle ϴ is a positive acute angle so, BC will be positive.

Now,  cos ϴ = 7k/25k = 7/25

tan ϴ = 24k/7k = 24/7

cosec ϴ = 25k/24k = 25/24

sec ϴ = 25k/7k = 25/7

cot ϴ = 7k/24k = 7/24

Relation Between Trigonometric Ratios

We know that the reciprocal of sin ϴ, cos ϴ, and tan ϴ is cosec ϴ, sec ϴ, and cot ϴ respectively. Therefore, some formulae are here which show the relation between them.

If we assume △PQR, 

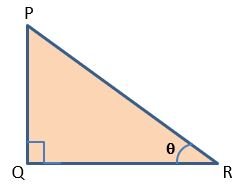
sin ϴ = PQ/PR    and cosec ϴ = PR/PQ

sin ϴ⨯cosec ϴ = (PQ/PR)⨯(PR/PQ)

sin ϴ⨯cosec ϴ = 1

Similarly,

1) sin ϴ×cosec ϴ = 1  ⇒   sin ϴ = 1/cosec ϴ and       cosec ϴ = 1/sin ϴ 

2) cos ϴ×sec ϴ = 1   ⇒     cos ϴ = 1/sec ϴ     and     sec ϴ = 1/cos ϴ 

3) tan ϴ×cot ϴ = 1   ⇒    tan ϴ = 1/cot ϴ     and     cot ϴ = 1/ tan ϴ 

4) tan ϴ = sin ϴ/cos ϴ

∵ sin ϴ = PQ/PR         and          cos ϴ = QR/PR

Now sin ϴ/cos ϴ = (PQ/PR) ∕ (QR/PR) = (PQ/PR)×(PR/QR) = PQ/QR = Perpendicular/Base = tan ϴ

Similarly,

5) cot ϴ = cos ϴ/sin ϴ

Trigonometric Identities

(1) sin² ϴ + cos² ϴ = 1

∵ sin ϴ = PQ/PR     and     cos ϴ = QR/PR [from the above figure △PQR]

LHS

sin² ϴ + cos² ϴ

(PQ/PR)² + (QR/PR)² 

PQ²/PR² + QR²/PR²

(PQ² + QR²)/PR²

PR²/PR²  = 1 = RHS            (by Pythagoras theorem PR² = PQ² + QR²)

(2) 1 + tan² ϴ = sec² ϴ

∵ tan ϴ = PQ/QR   [from the above figure △PQR]

LHS

1 + tan² ϴ

1 + (PQ/QR)²

(1 + PQ²)/QR²

(QR² + PQ²)/QR² 

PR²/QR² = (PR/QR)² = sec² ϴ = RHS

Alternate method –

We know that,  sin² ϴ + cos² ϴ = 1

Divide both sides by cos² ϴ

(sin² ϴ/cos² ϴ) + (cos² ϴ/cos² ϴ) = 1/cos² ϴ          (∵ tan ϴ = sin ϴ/cos ϴ)

tan² ϴ + 1 = sec² ϴ   

(3) 1 + cot² ϴ = cosec² ϴ

∵ cot ϴ = QR/PQ [from the above figure △PQR]

LHS   

1 + cot² ϴ

1 + (QR/PQ)²

1 + QR²/PQ² 

PQ² + QR²/PQ² 

PR²/PQ² = (PR/PQ)² = cosec² ϴ = RHS   

Alternate method –

We know that,  sin² ϴ + cos² ϴ = 1

Divide both sides by sin² ϴ

sin² ϴ/sin² ϴ + cos² ϴ/sin² ϴ = 1/sin² ϴ        (∵ cot ϴ = cos ϴ/sin ϴ)  

1 + cot² ϴ  = cosec² ϴ

Note – 1) (sin ϴ)² = sin² ϴ ≠ sin ϴ²

It means (sin ϴ)² can be written as sin² ϴ but cannot be written as sin ϴ². The same applies to other trigonometric functions.

2) Trigonometric identities can be written as –

sin2 ϴ + cos2 ϴ = 1	1 + tan2 ϴ = sec2 ϴ	1 + cot2 ϴ  = cosec2 ϴ
sin2 ϴ = 1 – cos2 ϴ	sec2 ϴ – tan2 ϴ = 1	cosec2 ϴ – cot2 ϴ = 1
cos2 ϴ = 1 – sin2 ϴ	tan2 ϴ = sec2 ϴ – 1	cot2 ϴ = cosec2 ϴ – 1

Example – If sin ϴ = 5/13 then find all the trigonometric functions using the relation between trigonometric ratios, where ϴ is an acute angle.

Solution – here, sin ϴ = 5/13 

We know that      sin² ϴ + cos² ϴ = 1

(5/13)² + cos² ϴ = 1

cos² ϴ = 1 – (25/169)

cos ϴ = √(169-25)/169 = √(144/169) = 12/13 

∵ sec ϴ = 1/cos ϴ  

sec ϴ = 1 ∕ 12/13 = 13/12  

∵ cosec ϴ = 1/sin ϴ = 1 ∕ 5/13 = 13/5  

∵ 1 + cot² ϴ = cosec² ϴ

cot² ϴ = cosec² ϴ – 1

cot ϴ = √(13/5)² – 1= √169/25 – 1 = √(169-25)/25 = √(144/25) = 12/5  

∵ tan ϴ = 1/cot ϴ

tan ϴ = 1 ∕ 12/5 = 5/12   

Examples Based on Trigonometric Identities

Example – 1) Prove that tan ϴ + cot ϴ = sec ϴ×cosec ϴ

Solution –  tan ϴ + cot ϴ = sec ϴ×cosec ϴ

LHS         tan ϴ + cot ϴ

sin ϴ/cos ϴ + cos ϴ/sin ϴ

(sin ϴ⨯sin ϴ + cos ϴ⨯cos ϴ)/cos ϴ⨯sin ϴ

(sin² ϴ + cos² ϴ)/cos ϴ⨯sin ϴ {∵ sin² ϴ + cos² ϴ = 1}

(1/cos ϴ)⨯sin ϴ = sec ϴ × cosec ϴ = RHS

Example – 2) Prove that (1 + cot² ϴ)(1 + cos ϴ)(1 – cos ϴ) = 1

Solution –  (1 + cot² ϴ)(1 + cos ϴ)(1 – cos ϴ) = 1

LHS      (1 + cot² ϴ)(1 + cos ϴ)(1 – cos ϴ) {∵ 1 + cot² ϴ = cosec² ϴ}

(cosec² ϴ)(1 – cos²ϴ)             {(a+b)(a-b) = a² – b²}

cosec² ϴ×sin² ϴ {∵ 1 – cos² ϴ = sin² ϴ}

(1/sin²ϴ)×sin²ϴ                      {cosec ϴ = 1/sin²ϴ}

1 = RHS

Trigonometric Ratios for Some Specific Angles

For all the trigonometric ratios we will find their values for some specific angles 0°, 30°, 45°, 60°, and 90°.

Trigonometric Ratios for Angle 0°

Let △ABC be a right-angled triangle in which ∠B is the right angle and ∠C is an acute angle ϴ. If the angle ϴ becomes 0° then line segment AC(Hypotenuse) will coincide with line segment BC(Base) and line segment AB(Perpendicular) will become 0. It means AB = 0 and AC = BC.

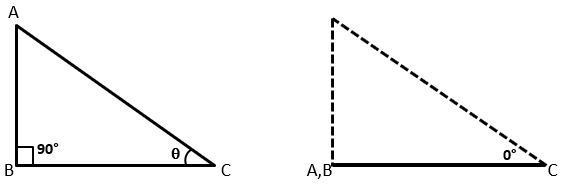
Thus, the values of trigonometric ratios for angle 0°

sin 0° = AB/AC = 0/AC = 0	cosec 0° = AC/AB = AC/0 = ∞ (infinitive)
cos 0° = BC/AC = BC/BC = 1	sec 0° = AC/BC = BC/BC = 1
tan 0° = AB/BC = 0/BC = 0	cot 0° = BC/AB = BC/0 = ∞ (infinitive)

Trigonometric Ratios for Angles 30° and 60°

Let △ABC be an equilateral triangle with each side 2a. Therefore AB=BC=CA=2a and ∠A=∠B=∠C=60°. AD is perpendicular on side BC from vertex A (AD ⊥ BC).

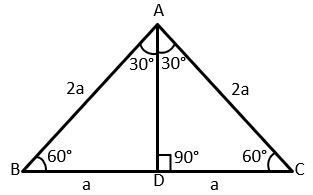
In △ABD and △ACD,

∠ADB = ∠ADC = 90°

AB = AC = 2a

AD = AD (Common side)

By RHS criterion, △ABD ≅ △ACD

Therefore, BD = CD = a and ∠BAD = ∠CAD = 30° (by CPCT)                       

In a right-angled triangle ABD,

AB = 2a, BD = a

AD² = AB² – BD² (by Pythagoras theorem)                                                      

AD² = (2a)² – (a)² = 4a² – a²

AD = √3a² 

AD = a√3

Trigonometric Ratios for Angle 30°

sin 30° = BD/AB = a/2a = 1/2	cosec 30° = AB/BD = 2a/a = 2
cos 30° = AD/AB = a√3/2a = √3/2	sec 30° = AB/AD = 2a/a√3 = 2/√3
tan 30° = BD/AD = a/a√3 = 1/√3	cot 30° = AD/BD = a√3/a = √3

Now, Trigonometric Ratios for Angle 60°

sin 60° = AD/AB = a√3/2a = √3/2	cosec 60° = AB/AD = 2a/a√3 = 2/√3
cos 60° = BD/AB = a/2a = 1/2	sec 60° = AB/BD = 2a/a = 2
tan 60° = AD/BD = a√3/a = √3	cot 60° = BD/AD = a/a√3 = 1/√3

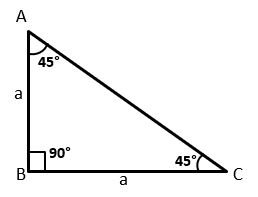
Trigonometric Ratios for Angle 45°

Let △ABC be a right-angled triangle. In which ∠B is the right angle and ∠C = 45°.

Now ∠A + ∠B + ∠C = 180°

∠A + 90° + 45° = 180°

∠A = 180° – 135°

∠A = 45° 

Since ∠A = ∠C

Therefore, AB = BC (opposite sides of equal angles are equal)

Let AB = BC = a

Then AC² = AB² + BC² (by Pythagoras theorem)

AC² = (a)² + (a)² = a² + a²

AC = √2a² = a√2

Thus, the values of trigonometric ratios for angle 45°

sin 45° = AB/AC = a/a√2 = 1/√2	cosec 45° = AC/AB = a√2/a = √2
cos 45° = BC/AC = a/a√2 = 1/√2	sec 45° = AC/BC = a√2/a = √2
tan 45° = AB/BC = a/a = 1	cot 45° = BC/AB = a/a = 1

Trigonometric Ratios for Angle 90°

Let △ABC be a right-angled triangle in which ∠B is the right angle and ∠C is an acute angle ϴ. If the angle ϴ becomes 90° then line segment AC(Hypotenuse) will coincide with line segment AB(Perpendicular) and line segment BC(Base) will become 0. it means BC = 0 and AC = AB.

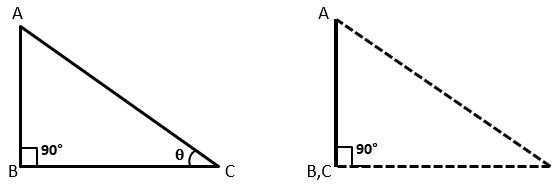
Thus, the values of trigonometric ratios for angle 90°

sin 90° = AB/AC = AB/AB = 1	cosec 90° = AC/AB = AB/AB = 1
cos 90° = BC/AC = 0/AC = 0	sec 90° = AC/BC = AC/0 = ∞ (infinitive)
tan 90° = AB/BC = AB/0 = ∞ (infinitive)	cot 90° = BC/AB = 0/AB = 0

From all the above values if we make a table so all these values will be remembered easily.

Trigonometric Ratios∖Angles (ϴ) (in Degree)➡ ⬇	0°	30°	45°	60°	90°
sin ϴ	0	1/2	1/√2	√3/2	1
cos ϴ	1	√3/2	1/√2	1/2	0
tan ϴ	0	1/√3	1	√3	∞
cosec ϴ	∞	2	√2	2/√3	1
sec ϴ	1	2/√3	√2	2	∞
cot ϴ	∞	√3	1	1/√3	0

Steps to Remember the Table Quickly –

1) First of all, we have to write numbers 0, 1, 2, 3, and 4 for the angles 0°, 30°, 45°, 60°, and 90° respectively.

2) After that we shall divide each number by 4 as follows

0/4 = 0

1/4

2/4 = 1/2

3/4

4/4 = 1

3) Now we have the numbers 0, 1/4, 1/2, 3/4, and 1. We shall take the square root of these numbers.

√0 = 0

√1/4 = 1/2

√1/2 = 1/√2

√3/4 = √3/2

√1 = 1

These values are for sin ϴ.

4) By writing these values in the reverse order we shall get the values for cos ϴ.

Reverse order →

1

√3/2

1/√2

1/2

0

5) For tan ϴ, we shall divide the values of sin ϴ by values of cos ϴ because tan ϴ = sin ϴ/cos ϴ.

0/1 = 0

1/2 ∕ √3/2 = 1/√3

1/√2 ∕ 1/√2 = 1

√3/2 ∕ 1/2 = √3

1/0 = ∞ (infinite)

6) Now we shall take the reciprocal of the values of sin ϴ to get the values of cosec ϴ because cosec ϴ = 1/sin ϴ.

Reciprocal →

1/0 = ∞ (infinite)

1 ∕ 1/2 = 2

1 ∕ 1/√2 = √2

1 ∕ √3/2 = 2/√3

1/1 = 1

7) For sec ϴ, we shall write the values of cosec ϴ in the reverse order.

Reverse order →

1

2/√3

√2

2

∞ (infinite)

8) For cot ϴ, we shall take the reciprocal of the values of tan ϴ because cot ϴ = 1/tan ϴ.

Reciprocal →

1/0 = ∞ (infinite)

1 ∕ 1/√3 = √3

1/1 = 1

1/√3

0/1 = 0

Example – 1) find the value of sin 60° cos 30° – sin 30° cos 60°.

Solution – sin 60° cos 30° – sin 30° cos 60°

(√3/2)⨯(√3/2) – (1/2)⨯(1/2) = 3/4 – 1/4 = (3-1)/4 = 2/4 = 1/2 Ans. 

Example – 2) find the value of tan² 45° + sin² 30° – cos² 60°

Solution – tan² 45° + sin² 30° – cos² 60°

(1)² + (1/2)² – (1/2)² = 1 + 1/4 – 1/4 = 1 Ans.

Trigonometric Ratios of Complementary Angles

When the sum of two angles is 90° they are called Complementary Angles. If any acute angle is A then its complementary angle will be (90° – A).  

Let △PQR be a right-angled triangle in which ∠Q is the right angle and ∠R is the acute angle ϴ.

So,   ∠P + ∠R = 90°

∠P + ϴ = 90°

∠P = (90° – ϴ)

Therefore ∠P and ∠R are complementary angles.

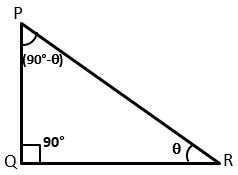
Now trigonometric ratios for angle ϴ

sin ϴ = PQ/PR                 cos ϴ = QR/PR             tan ϴ = PQ/QR                 

cosec ϴ = PR/PQ             sec ϴ = PR/QR            cot ϴ = QR/PQ …………….(1)

Trigonometric ratios for angle (90° – ϴ)      

sin (90° – ϴ) = QR/PR              cos (90° – ϴ) = PQ/PR            tan (90° – ϴ) = QR/PQ               

cosec (90° – ϴ) = PR/QR          sec (90° – ϴ) = PR/PQ            cot (90° – ϴ) = PQ/QR …………..(2)

By comparing equations (1) and (2),

sin (90° – ϴ) = QR/PR = cos ϴ             cos (90° – ϴ) = PQ/PR = sin ϴ

tan (90° – ϴ) = QR/PQ = cot ϴ                 cot (90° – ϴ) = PQ/QR = tan ϴ

cosec (90° – ϴ) = PR/QR = sec ϴ              sec (90° – ϴ) = PR/PQ = cosec ϴ

Therefore,

sin (90° – ϴ) = cos ϴ	cos (90° – ϴ) = sin ϴ
tan (90° – ϴ) = cot ϴ	cot (90° – ϴ) = tan ϴ
cosec (90° – ϴ) = sec ϴ	sec (90° – ϴ) = cosec ϴ

Note – It means sin and cos, tan and cot, cosec and sec are equal for complementary angles.

Some Examples –

Example – 1) Solve sin 35°/cos 55° 

Solution – ∵ 55° = 90° – 35°

∴ cos 55° = cos(90° – 35°)            [∵ cos (90° – ϴ) = sin ϴ]

cos 55° = sin 35°

So,  sin 35°/sin 35° = 1        Ans.         

Example – 2) Solve cos² 50° + cos² 40°

Solution – ∵ 50° = 90° – 40°

∴ cos 50° = cos (90° – 40°) = sin 40°

And cos² 50° = sin² 40°

Therefore,    cos² 50° + cos² 40°

sin² 40° + cos² 40° = 1        [∵ sin² ϴ + cos² ϴ = 1] Ans.

Example – 3) Prove that tan 25° tan 55° tan 65° tan 35° = 1

Solution – LHS = tan 25° tan 55° tan 65° tan 35°

= tan (90° – 65°) tan (90° – 35°) tan 65° tan 35°

= cot 65° cot 35° tan 65° tan 35°

= 1/(tan 65° tan 35°) × tan 65° tan 35°

= 1

= RHS

Application of Trigonometry

Trigonometry is used in many different fields such as Astronomy, Navigation, Surveying, Periodic Functions, Optics, Acoustics, etc.

Height and Distance

Here, we will use trigonometry to find the heights and distances of various objects without actually measuring them.

Some Important Terms

(1) Line of sight –  The line drawn from the eye of the observer to the point of the object is called the line of sight.

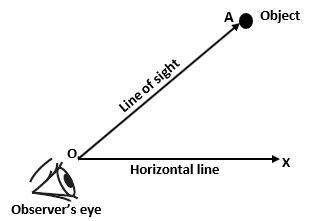
In the above figure, Observer’s eye is at O point and the Object is at A point then OA will be the Line of sight. OX is the horizontal line.

(2) The angle of elevation – When the object is above the eye and we raise our head to see the object then the angle formed between the line of sight and the horizontal line is called the Angle of Elevation. It is also called the angular height of the object. In this condition, the object will be above the horizontal line.

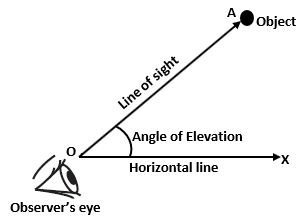
∠AOX is the angle made between the line of sight OA and the horizontal line OX.

Therefore, Angle of Elevation = ∠AOX

(3) The Angle of depression – When the object is below the eye and we lower our head to see the object then the angle formed between the line of sight and the horizontal line is called the Angle of Depression. In this condition, the object will be below the horizontal line.

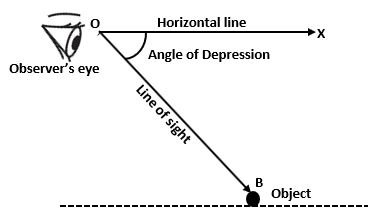
∠BOX is the angle made by the line of sight OB and horizontal line OX.

Therefore, Angle of Depression = ∠BOX

Example – 1) The angle of elevation of the top of a tower from a point on the Ground is 45° and the distance of this point from the base of the tower is 60 m. find the height of the tower.

Solution –

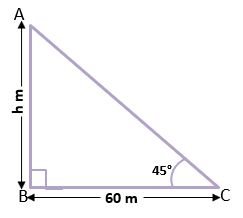
Let the height of tower AB be h meter.

Distance (BC) = 60 m

Angle of Elevation ∠ACB = 45°

In the right-angled triangle ABC,

tan 45° = AB/BC

1 = h/60                                                                                                    

h = 60 m

So, the height of tower AB is 60 m.            Ans.

Note – In the above example, the perpendicular side and base side are used in the right-angled triangle so we have used the trigonometric function tan ϴ. cot ϴ can be also used. All the questions will be solved like this.

Example – 2) The height of a vertical pillar is equal to its shadow. Find the angle of elevation of the sun.

Solution –

Let the angle of elevation of the sun be ϴ.

AC is a vertical pillar and BC is its shadow.

According to the question,

Height of vertical pillar(AC) = length of shadow(BC)

In △ABC,

tan ϴ = AC/BC

tan ϴ = AC/AC = 1               [∵ tan 45° = 1         

tan ϴ = tan 45°         

      ϴ = 45° 

So, the angle of elevation of the sun is 45°.  Ans.

Example – 3) From the top of the 10 m high tower, the angle of depression at a point on Earth is 60°. Find the distance of the point from the base of the tower.

Solution –

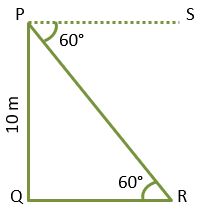
Here, the height of tower PQ = 10 m

We have to find distance QR.

PS is the horizontal line because the angle of depression is given from the top of the tower.

∠SPR = ∠PRQ = 60° (Alternate angles)

In △PQR,

tan 60° = PQ/QR

√3 = 10/QR

QR = 10/√3     

QR = (10/√3)⨯(√3/√3)      (on Rationalization)

QR = 10√3/3 = 3.33⨯1.732               [∵ √3 = 1.732]

QR = 5.767 m

Thus the distance of the point from the base of the tower is 5.767 m.      Ans.

Trigonometry Class 10^th in Hindi

More About Trigonometry