Trigonometric Ratios of Acute Angles Class 10th

Introduction

In a right-angled triangle, the ratio of any two sides is known as the Trigonometric Ratios of Acute angles. Each trigonometric function has a different ratio.

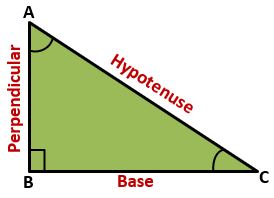
Base (BC) – Adjacent side of ∠C

Perpendicular (AB) – opposite side of ∠C

Hypotenuse (AC) – opposite side of ∠B(right angle)

In the above right-angled triangle, ∠B is a right angle and there are two acute angles ∠A and ∠C. for both acute angles trigonometric ratios can be found.

Trigonometric Ratios of Acute Angle ∠C

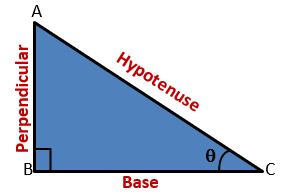
Let ∠C = ϴ

1) sin ϴ = Perpendicular/Hypotenuse = AB/AC  

2) cos ϴ = Base/Hypotenuse = BC/AC  

3) tan ϴ = Perpendicular/Base = AB/BC                          

4) cosec ϴ = Hypotenuse/Perpendicular = AC/AB  

5) sec ϴ = Hypotenuse/Base = AC/BC  

6) cot ϴ = Base/Perpendicular = BC/AB

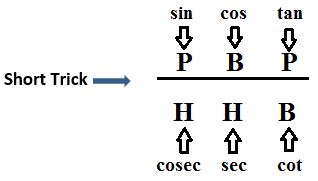
We can also find all the trigonometric ratios for the acute angle A. for acute angle A Base (Adjacent side of ∠A) will be AB and the Perpendicular (opposite side of ∠A) will be BC. hypotenuse will remain the same (AC).

Note – 1) In Trigonometry, trigonometric ratios depend on the acute angle ϴ, not on the size of the Right-angled triangle.

2) The trigonometric ratios are unique for each acute angle ϴ.

3) sin ϴ ≠ sin⨯ϴ , cos ϴ ≠ cos⨯ϴ, tan ϴ ≠ tan⨯ϴ

It is not multiplication between trigonometric function and acute angle.

4) Trigonometric ratios of any positive acute angle are always positive.

Some Examples –

Example – 1) In △ABC, ∠C is a right angle. side AB = 5 cm and BC = 4 cm then find all trigonometric ratios of angle A.

Solution –

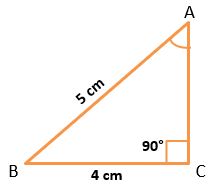
∵ △ABC is a right-angled triangle.

By Pythagoras theorem,

AC² = AB² – BC²

AC = √(5)² – (4)²

AC = √(25-16) = √9 = 3 cm

Now,

sin A = BC/AB = 4/5	cosec A = AB/BC = 5/4 (Reciprocal of sin A)
cos A = AC/AB = 3/5	sec A = AB/AC = 5/3 (Reciprocal of cos A)
tan A = BC/AC = 4/3	cot A = AC/BC = 3/4 (Reciprocal of tan A)

Ans.

Example – 2) if sin ϴ = 24/25, then find the remaining trigonometric ratios of ϴ.

Solution – sin ϴ = 24/25 = Perpendicular/Hypotenuse

If we draw △ABC for sin ϴ = 24/25

Perpendicular = AB      and      Hypotenuse = AC

Let AB = 24k, AC = 25k

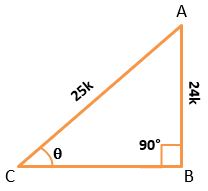
Where k = proportionality constant

In △ABC By Pythagoras theorem,

BC = √(AC)² – (AB)²                 

BC = √(25k)² – (24k)²                              

BC = √625k² – 576k²                      

BC = √49k² 

BC = ±7k

since angle ϴ is an acute angle so, BC will be positive.

Now  cos ϴ = 7k/25k = 7/25

tan ϴ = 24k/7k = 24/7

cosec ϴ = 25k/24k = 25/24

sec ϴ = 25k/7k = 25/7

cot ϴ = 7k/24k = 7/24 Ans.

Trigonometric Ratios of Acute Angles Class 10^th in Hindi

More About Trigonometric Ratios of Acute Angles