Circumference of Circle Class 10th

Introduction

In our daily life, we use many circular objects like rubber rings, bangles, coins, wheels, etc. If we want to measure their circular length then how can we do it? Here’s an activity to understand it clearly. If we have to measure the circular length (Circumference of Circle) of a wheel then we shall put the wheel on the floor and mark a point P on it where it is touching the floor as shown in the figure.

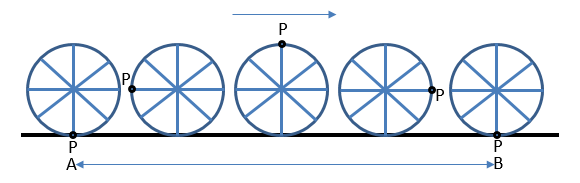
Now we rotate the wheel in one direction. Point P is also rotating with the wheel which we can see in the figure. In one rotation, when point P comes again in the first position, we shall stop the wheel. The distance from the starting point to the endpoint is AB. This Distance will be equal to the circular length of the wheel.

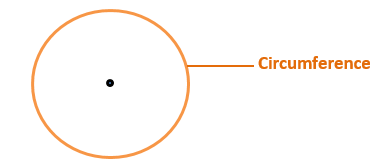
This circular length of the wheel is called the Circumference of the Circle. This is also known as the Perimeter of the Circle.

The Formula of Circumference of Circle

If we consider that the wheel rotates with respect to the Centre of the wheel and the radius(r) of the wheel completes one rotation and the angle made in one rotation is 2π (360°) then

Circumference of Circle = 2π×r = 2πr

And Diameter (D) of the wheel completes one rotation with angle π (180°) then

Circumference of Circle = π×D = πD

Or circumference/diameter = π [Ratio of Circumference and Diameter is constant (π)]

It means we can say that the circumference of any circular object is equal to the distance covered in one rotation.

Note – 1) Radius is half of the Diameter.

2) The value of π is 22/7 which is equal to 3.14(Approximately). The more accurate value of π is 3.1416 given by the great Indian mathematician Aryabhatta.

3) π is an irrational number because its Decimal expansion is non-terminating non-repeating (non-recurring).

Some Examples

Example 1) Find the circumference of the circle whose radius is 7 cm.

Solution – Given Radius (r) = 7 cm

Circumference of Circle = 2πr  

= 2×22/7×7

= 2×22

= 44 cm.                                      

So, the Circumference of the Circle is 44 cm.           Ans.

Note – We use the value of π = 22/7 if not given in the question.

Example 2) The Circumference of the Circle is 154 cm. Find its Diameter.

Solution – Here, Circumference of Circle = 154 cm

So, 2πr = 154 cm

2×22/7×r = 154

r = 154×7 / 2×22

r = 7×7 / 2 = 49/2 cm

We know Diameter (D) = 2×r

D = 2×49/2

D = 49 cm

Therefore, the Diameter of the circle is 49 cm.              Ans.

Example 3) A wheel of a bicycle makes 4000 rotations to complete a distance of 12 km. Find the Radius of the wheel.

Solution – Given, Number of rotations = 4000

Distance covered = 12 km

The radius of the wheel (r) =?

∵ Distance covered in 4000 rotations = 12 km

∴ Distance covered in 1 rotation = 12/4000 km = (12/4000) ×1000×100 cm

So, Distance covered in 1 rotation = 300 cm

We know that the Circumference of a circle = Distance covered in one rotation

2πr = 300 cm  

2×22/7×r = 300 cm

r = 300×7 / 2×22 = 150×7 / 22 = 75×7 / 11 = 525/11

r = 47.72 cm

Hence, the Radius of the wheel is 47.72 cm.            Ans.

Perimeter of Semicircle

Instead of circumference, the perimeter is a more suitable word for semicircle because it includes Diameter also.  

The perimeter of the semicircle is the sum of half Circular Distance and Diameter.

Now half Circular Distance of semicircle = half of circumference of circle = 2πr/2 = πr = πD/2

And Diameter = D = 2r

So, the Perimeter of the Semicircle = πD/2 + D

Or Perimeter of the Semicircle = πr + 2r

Some Examples

Example 1) The radius of a semicircle-shaped park is 35 cm. Find its Perimeter.

Solution – Radius (r) = 35 cm

Perimeter of semicircle shaped park = πr + 2r   

= 22/7 ×35 + 2×35

= 22×5 + 70

= 110 + 70

= 180 cm

Therefore, the Perimeter of the semicircle-shaped park is 180 cm.             Ans.

Example 2) Diameter of a Semicircle is 14 cm. Find Perimeter.

Solution – Here, Diameter (D) = 14 cm

So, Perimeter of Semicircle = πD/2 + D

= (22/7)×(14/2) + 14 = 11×2 + 14

= 22 + 14

= 36 cm

So, the Perimeter of the Semicircle is 36 cm.             Ans.

Example 3) If the Perimeter of a semicircle is 144 cm, then find its radius.

Solution – Perimeter of the semicircle = 144 cm

πr + 2r = 144 cm 

22/7 ×r + 2×r = 144 cm  

r(22/7 + 2) = 144

r{(22+14)/7} = 144

r(36/7) = 144

r = 144×7/36

r = 4×7

r = 28 cm

Thus, the radius of the semicircle is 28 cm.             Ans.

Circumference of Circle Class 10^th in Hindi

More About Circumference of Circle