Some Applications of Trigonometry Class 10th

Applications of Trigonometry

Introduction

There are many applications of trigonometry but we shall study some of them in this section. Trigonometry is used in many different fields such as Astronomy, Navigation, surveying, Periodic functions, Optics, acoustics, etc. Here, we shall use trigonometry to find the Height and Distance of various objects without actually measuring them.

Some Important Terms

(1) Line of Sight –  The line drawn from the eye of the observer to the point of the object is called the line of sight.

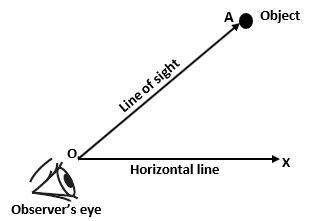
In the above figure, Observer’s eye is at O point and the Object is at A point then OA will be the Line of sight. OX is the horizontal line.

(2) The Angle of Elevation – When the object is above the eye and we raise our head to see the object then the angle formed by the line of sight and the horizontal line is called the angle of elevation. It is also called the angular height of the object. In this condition, the object will be above the horizontal line.

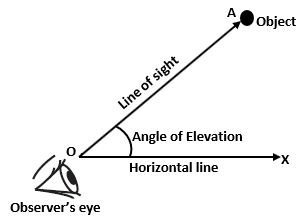
∠AOX is the angle made by the line of sight OA and horizontal line OX.

Therefore, Angle of Elevation = ∠AOX

(3) The Angle of Depression – When the object is below the eye and we lower our head to see the object then the angle formed by the line of sight and the horizontal line is called the angle of depression. In this condition, the object will be below the horizontal line.

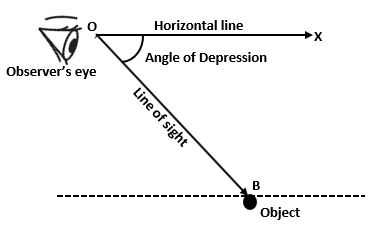
∠BOX is the angle made by the line of sight OB and horizontal line OX.

Therefore, Angle of Depression = ∠BOX

Some Examples –

Example – 1) The angle of elevation of the top of a tower from a point on the Ground is 45° and the distance of this point from the base of the tower is 60 m. find the height of the tower.

Solution –

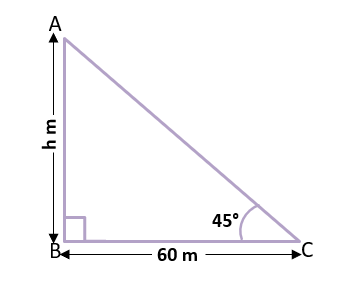
Let the height of tower AB be h meter.

Distance (BC) = 60 m

Angle of Elevation ∠ACB = 45°

In the right-angled triangle ABC,

tan 45° = AB/BC

1 = h/60                                                                                                    

h = 60 m

So, the height of tower AB is 60 m.               Ans.

Note – In the above example, the perpendicular side and base side are used in the right-angled triangle so we have used the trigonometric function tan ϴ. cot ϴ can be also used. All the questions will be solved like this.

Example – 2) The height of a vertical pillar is equal to its shadow. Find the angle of elevation of the sun.

Solution –

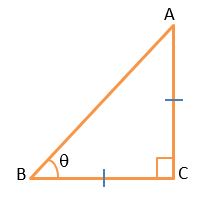
Let the angle of elevation of the sun be ϴ.

AC is a vertical pillar and BC is its shadow.

According to the question,

Height of vertical pillar(AC) = length of shadow(BC)

In △ABC,

tan ϴ = AC/BC

tan ϴ = AC/AC = 1               [∵ tan 45° = 1         

tan ϴ = tan 45°         

      ϴ = 45° 

So, the angle of elevation of the sun is 45°.  Ans.

Example – 3) From the top of the 10 m high tower, the angle of depression at a point on Earth is 60°. Find the distance of the point from the base of the tower.

Solution –

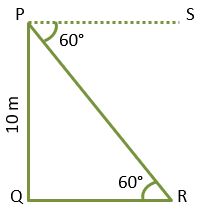
Here, the height of tower PQ = 10 m

We have to find the distance QR.

PS is the horizontal line because the angle of depression is given from the top of the tower.

∠SPR = ∠PRQ = 60° (Alternate angles)

In △PQR,

tan 60° = PQ/QR

√3 = 10/QR

QR = 10/√3     

QR = (10/√3)⨯(√3/√3)      (on Rationalization)

QR = 10√3/3 = 3.33⨯1.732               [∵ √3 = 1.732]

QR = 5.767 m

Thus the distance of the point from the base of the tower is 5.767 m.      Ans.

Some Applications of Trigonometry Class 10^th in Hindi

More About Applications of Trigonometry