Areas Related to Circles Class 10th

Introduction

We have already studied some methods to find the perimeter and area of different types of plane figures like square, rectangle, triangle, circle, trapezium, rhombus, etc. in the previous classes. In our daily life, we see many circular objects like rings, bangles, plates, wheels, roti, etc. All these objects are helpful in studying circular shapes. In this topic, we shall study the perimeter and area of the circle and areas related to the part of circles which are known as sector and segment. We shall also study the area of combined plane figures including circles or their parts.

The Perimeter of a Circle

As we know that the circular distance of a circle that is completed in a round is called the perimeter of a circle. For a circle, we usually use the word ‘circumference’ instead of perimeter. The circumference of a circle is given as the formula written below.

The circumference of a circle = 2πr

Where, r = radius of the circle

π (pi) = constant

The value of π is 22/7 or 3.1416 (approximately).

We can write, circumference / 2r = π

Or circumference/diameter = π (since the diameter is double the radius)

Note – 1) The ratio of circumference and diameter is equal to π which is a constant.

2) π is an irrational number because its decimal expansion is non-terminating non-repeating (non-recurring).

Example – The radius of a circle is 7 cm. Find its circumference.

Solution – Radius (r) = 7 cm.

The circumference of a circle = 2πr

= 2×(22/7)×7

= 2×22 = 44 cm.                Ans.

Area of a Circle

The surface covered under the circular region of a circle is called the area of a circle. The area of a circle is given as the formula below.

The area of a circle = πr²

Example – The diameter of a circular plate is 14 cm. Find the area of the circular plate.

Solution – Since diameter (D) = 14 cm.

Therefore, radius (r) = 14/2 = 7 cm.

Now, the area of the circular plate = πr²

= (22/7)×7×7

= 22×7 = 154 cm²                 Ans.

The Sector of a Circle

The part of a circle that is made by two radii and their corresponding arc is called the sector of a circle. Let’s understand this with the help of a figure.

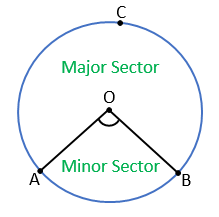
A circle with Centre O is given. There are two radii OA and OB and the corresponding arc is AB in this circle. The part made by these two radii and the corresponding arc is OAB which is called the sector of this circle. The angle made between two radii is called the angle of the sector. The two radii divide the circle into two sectors called the minor sector and the major sector. The two radii also divide the circular length into two arcs which are called minor arc and major arc.

In the above figure,

OAB = Minor sector of the circle

∠AOB = Angle of the minor sector

OACB = Major sector of the circle

AB = Minor arc

ACB = Major arc

The angle of the major sector can be found by subtracting the ∠AOB from 360°. So, the angle of the major sector is 360° – ∠AOB.

Area of Sector of a Circle

To find the area of the sector of a circle we shall derive the formula with the help of a method discussed below.

Let a circle with Centre O is given in the figure. The radius of this circle is r and the angle of the sector OAB is ϴ or ∠AOB = ϴ.

We know that the area of a circle is πr². If we consider the whole circle as a sector then the angle made at the Centre which is 360° will be the angle of the sector.

Now, using the unitary method

If the angle of the sector (Centre) is 360°, then the area of the sector (circle) = πr²

If the angle of the sector is 1°, then the area of the sector = πr²/360°

And if the angle of the sector is ϴ, then the area of the sector = (πr²/360°)×ϴ

Therefore, the formula to find the area of the sector of angle ϴ of a circle

Area of the sector of a circle = πr²×ϴ / 360°

With the help of the value of radius r and angle ϴ, we can calculate the area of the minor sector and major sector.

Note – 1) We can use the above formula when ϴ is given in degree. If ϴ is given in radian then we can convert the formula by replacing 360° with 2π because in radian, 360° = 2π. Then the formula will be.

Area of the sector of a circle = πr²×ϴ / 2π

Or we can write, Area of the sector of a circle = r²×ϴ / 2

2) Area of the minor sector = πr² – the area of the major sector

3) Area of the major sector = πr² – the area of the minor sector  

We can also find the length of the arc AB of the sector OAB with the help of the unitary method same as the above explanation.

We know that the circumference of a circle is 2πr. If we consider the whole circular length of the circle as an arc then the angle made at the Centre which is 360° will be the angle of the sector.

Now, using the unitary method

If the angle of the sector (Centre) is 360°, then the length of the arc (circumference) = 2πr

If the angle of the sector is 1°, then the length of the arc = 2πr/360°

And if the angle of the sector is ϴ, then the length of the arc = (2πr/360°)×ϴ

Therefore, the formula to find the length of the arc corresponding to angle ϴ of a circle

Length of an arc of a circle = 2πr×ϴ / 360°

With the help of the value of radius r and angle ϴ, we can calculate the length of the minor arc and major arc.

Note – 1) When ϴ is in radian, then the length of an arc of a circle = 2πr×ϴ / 2π

Or we can write, length of an arc of a circle = r×ϴ

2) Length of the minor arc = 2πr – length of the major arc

3) Length of the major arc = 2πr – length of the minor arc

Examples –

The Segment of a Circle

Area of Segment of a Circle

Area of Combined Plane Figures

Areas Related to Circles Class 10th in Hindi

More About Areas Related to Circles