Distance Between Two Points in Cartesian Plane and Distance Formula Class 10th

Introduction

In Coordinate Geometry, If there are two points situated in the Cartesian plane and we have to find the distance between them, then we can find the distance with the help of the Distance Formula. let’s see how we can find it.

If Two Points are Situated on the Coordinate Axis (Whether on the x-axis or y-axis)

If two points are situated on the x-axis or y-axis then we can easily find the distance between them by taking the Difference. Let there be two points A and B situated on the x-axis and two points C and D situated on the y–axis.

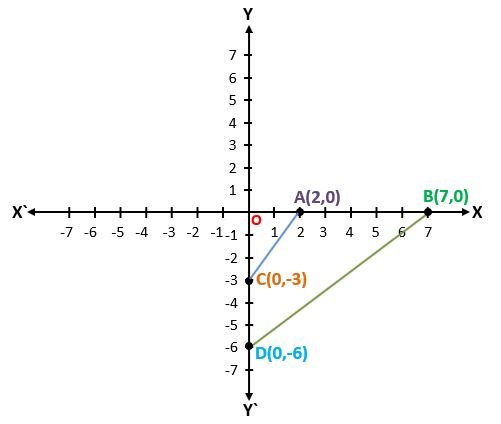
Coordinates of point A = (2,0)      and       Coordinates of point B = (7,0)

Coordinates of point C = (0,-3)     and       Coordinates of point D = (0,-6)

It means the distance of point A from Origin OA = 2 units

and distance of point B from Origin OB = 7 units

Therefore distance between points A and B, here OB > OA,    AB = OB – OA = 7 – 2 = 5 units

Similarly, OC = -3 units and OD = -6 units (Here, – sign shows the negative direction)  

So, the distance between points C and D, here OC > OD, CD = OC – OD = -3 – (-6) = -3 + 6 = 3 units

We can also find the distance between points A & C and points B & D with the help of the Pythagoras theorem (Boudhayana theorem).

At first, we shall join point A to point C and point B to point D. now we can see there are two right-angled triangles AOC and BOD. By Pythagoras theorem,

In △AOC,  AC² = OA² + OC²

AC = √(2)² + (-3)² = √(4+9) = √13 units

In △BOD,  BD² = OB² + OD²

BD = √(7)² + (-6)² = √(49+36) = √85 units

We saw that if two points are situated on Coordinate axes then we can easily find the distance between them.

If Two Points are not Situated on the Coordinate Axis (Situated in the Quadrant)

Let there be two points P(2,3) and Q(7,5) situated in Quadrant I. to find the distance between points P and Q, we draw perpendicular PR and QS on the x-axis from points P and Q respectively. We also draw perpendicular PT on QS from point P.

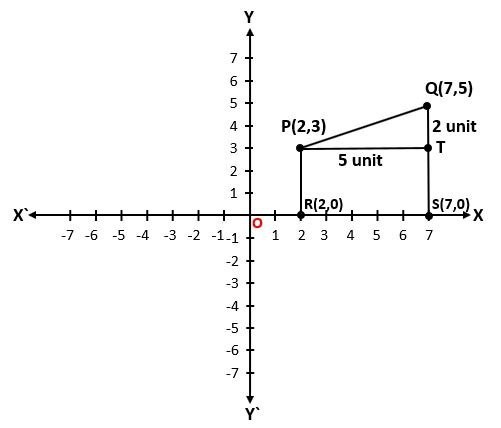
The coordinates of points R and S are (2,0) and (7,0) respectively.

Here, RS = OS – OR = 7 – 2 = 5 units = PT    [∵ RS = PT]

QS = 5 units and PR = 3 units = TS     [∵ PR = TS]

QT = QS – TS = 5 – 3 = 2 units

By Pythagoras theorem, in △PQT,

PQ² = PT² + QT² = (5)² + (2)²

PQ = √(25+4) 

PQ = √29 units

Distance Formula

Let us consider two points A(x₁,y₁) and B(x₂,y₂) situated in Quadrant I and we have to find the distance AB.

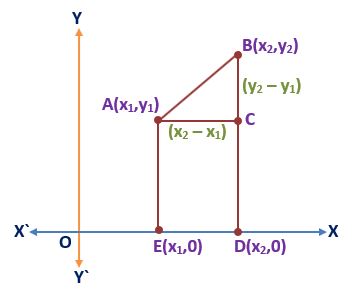
We draw perpendicular AE and BD on the x-axis from points A and B respectively and draw perpendicular AC on BD from point A.

Here,  ED = (x₂ – x₁) units

Since ED = AC, therefore AC = (x₂ – x₁) units    and    BD = y₂ units

 AE = CD = y₁ units and BC = BD – CD = (y₂ – y₁) units

In △ABC, by Pythagoras theorem,

AB² = AC² + BC²

AB² = (x₂ – x₁)² + (y₂ – y₁)²

AB = √(x₂ – x₁)² + (y₂ – y₁)²

This expression is called Distance Formula. Because Distance is always positive so we shall take only the positive value of the square root.

We can also write,

AB = √(Difference of x-coordinates)² + (Difference of y-coordinates)²

Note – 1) Distance of a point A(x,y) from Origin O(0,0) can be written as expression

OA = √(x – 0)² + (y – 0)²

OA = √x² + y²

2) The Distance formula can be also written as

AB = √(x₁ – x₂)² + (y₁ – y₂)²

Because the square of any difference whether negative or positive is always positive.

Let’s Take Some Examples –

Example 1) Find the distance between points P(2,9) and Q(7,-3).

Solution – Let us compare it with P(x₁,y₁) and Q(x₂,y₂) then

x₁ = 2, y₁ = 9, x₂ = 7, y₂ = -3

By Distance formula,   PQ = √(x₂ – x₁)² + (y₂ – y₁)² 

PQ = √(7 – 2)² + (-3 – 9)²

PQ = √(5)² + (-12)² 

PQ = √(25+144)

PQ = √169 

PQ = 13 units

So, the distance between points P and Q is 13 units.           Ans.

Example 2) Find the value of x if the Distance between points (1,3) and (x,7) is 5 units.

Solution – Let the given points be A(1,3) and B(x,7).

Distance AB = 5 units, here x₁ = 1, y₁ = 3, x₂ = x, y₂ = 7

By Distance formula, AB = √(x₂ – x₁)² + (y₂ – y₁)²

Putting the values,     5 = √(x – 1)² + (7 – 3)²   

5 = √(x² – 2x + 1) + (4)²         [∵ (a – b)² = a² – 2ab + b²]

5 = √(x² – 2x + 1 + 16)

5 = √(x² – 2x + 17) 

Squaring both sides

(5)² = {√(x² – 2x + 17)}²

25 = x² – 2x + 17

x² – 2x + 17 = 25

x² – 2x + 17 – 25 = 0

x² – 2x – 8 = 0

x² – 4x + 2x – 8 = 0     [By factorization method]

x(x – 4) + 2(x – 4) = 0

(x – 4)(x + 2) = 0

(x – 4) = 0      and       (x + 2) = 0

x = 4          and         x = -2

So, the values of x are 4 and -2.             Ans.

Example 3) Show that the points (-2,1), (2,4), and (5,-2) are the vertices of a triangle.

Solution – Let the points P(-2,1), Q(2,4), and R(5,-2) be the vertices of a triangle. We shall find the Distance PQ, QR, and PR.

By the Distance formula,

PQ = √{2 – (-2)}² + (4 – 1)² = √{2+2}² + (3)² = √{4}²+9 = √(16+9) = √25 = 5

QR = √(5 – 2)² + (-2 – 4)² = √(3)² + (-6)² = √(9+36) = √45 = 6.71 (Approximately)

PR = √{5 – (-2)}² + (-2 – 1)² = √{5+2}² + (-3)² = √{7}²+9 = √(49+9) = √58 = 7.62 (Approximately)

We know that the sum of any two sides of a triangle is always greater than the third side.

Here, the sum of any two distances is greater than the third distance so the given points are the vertices of a triangle.              Ans.

Example 4) Show that the points S(-2,5), T(-4,4), U(-1,-2), and V(1,-1) are the vertices of a Rectangle.

Solution –

To prove it is a rectangle we shall find the distances of all four sides and both the diagonals and if the Distances of opposite sides are equal and the distances of both diagonals are equal then it will be a rectangle. So, by the Distance formula,

ST = √{-4 – (-2)}² + (4 – 5)² = √{-4+2}² + (-1)² = √{-2}²+1 = √(4+1) = √5

TU = √{-1 – (-4)}² + (-2 – 4)² = √{-1+4}² + (-6)² = √{3}²+36 = √(9+36) = √45

UV = √{1 – (-1)}² + {-1 – (-2)}² = √{1+1}² + {-1+2}² = √{2}²+{1}² = √(4+1) = √5

VS = √(-2 – 1)² + {5 – (-1)}² = √(-3)² + {5+1}² = √9+{6}² = √(9+36) = √45

Here, opposite sides are equal.

Now Diagonals

SU = √{-1 – (-2)}² + (-2 – 5)² = √{-1+2}² + (-7)² = √{1}²+49 = √(1+49) = √50

TV = √{1 – (-4)}² + (-1 – 4)² = √{1+4}² + (-5)² = √{5}²+25 = √(25+25) = √50

So, Diagonals are also equal.

Therefore, S, T, U, and V are the vertices of a Rectangle.                  Ans.

Example 5) If the point (x,y) is equidistant from the points (5,-4) and (-1,6) then find the relation between x and y.

Solution – Let point A(x,y) be equidistant from the points P(5,-4) and Q(-1,6).

It is given that   Distance PA = Distance QA          [∵ Distance formula AB = √(x₂ – x₁)² + (y₂ – y₁)²

Or we can write, PA² = QA²         [∴ AB² = (x₂ – x₁)² + (y₂ – y₁)²        

By Distance formula, 

(5 – x)² + (-4 – y)² = (-1 – x)² + (6 – y)²                            

25 – 10x + x² + 16 + 8y + y² = 1 + 2x + x² + 36 – 12y + y²             [∵ (a – b)² = a² – 2ab + b²]

41 – 10x + 8y = 37 + 2x – 12y

41 – 10x + 8y – 37 – 2x + 12y = 0

-12x + 20y + 4 = 0

Or    12x – 20y – 4 = 0

4[3x – 5y – 1] = 0

3x – 5y – 1 = 0

3x – 5y = 1

This is the required equation that shows the relation between x and y.        Ans.

Example 6) Find a point on the x-axis that is equidistant from points A(3,2) and B(4,-6).

Solution – Since we know that the coordinate of a point situated on the x-axis is of the form (x, 0).

So, Let the point P(x,0) be situated on the x-axis.

According to the question,    PA = PB

Or we can write,    PA² = PB²

By Distance formula, (3 – x)² + (2 – 0)² = (4 – x)² + (-6 – 0)²

9 – 6x + x² + 4 = 16 – 8x + x² + 36           [∵ (a – b)² = a² – 2ab + b²]

13 – 6x = 52 – 8x

-6x + 8x = 52 – 13

2x = 39

x = 39/2

Thus the point on the x-axis is P(39/2, 0).            Ans.

Distance Formula Class 10^th in Hindi

More About Distance Formula