Number System Class 9th

In the previous classes, we studied the number system. We know the types of numbers, number lines, and how to represent different types of numbers on the number line. We have studied natural numbers, whole numbers, integers, rational numbers, etc. In class 9^th, we will study more about the number system but before that let us recall the types of numbers and number lines.

Types of Numbers

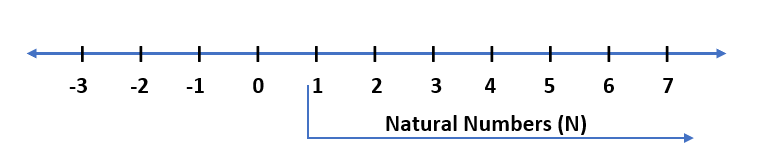
(1) Natural Numbers – All the counting numbers starting from 1 are called natural numbers or we can also say that numbers from 1 to ∞ (infinitive) are called natural numbers. Natural numbers are denoted by N.

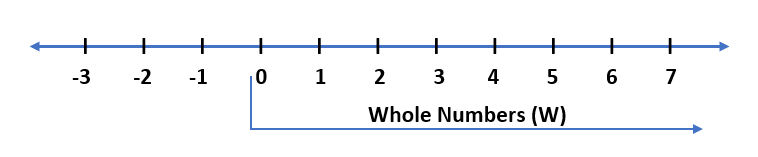
(2) Whole Numbers – All the counting numbers including 0 are called whole numbers or numbers from 0 to ∞ are called whole numbers. Whole numbers are denoted by W.

(3) Integers – All the positive and negative numbers including 0 are called integers or collections of all the negative numbers and whole numbers are called integers. Integers are denoted by Z. A German word ‘Zahlen’ means ‘to count’, that’s why integers are denoted by Z. On the number line, positive numbers are called positive integers and negative numbers are called negative integers.

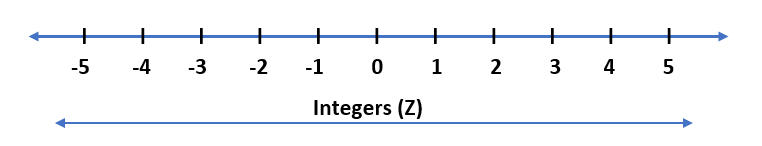
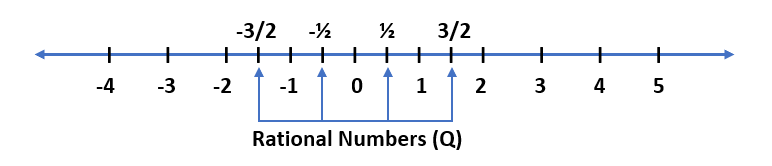
(4) Rational Numbers – If a number can be written in the form of p/q, then the number is called a rational number, where p and q are integers and q ≠ 0. Rational numbers are denoted by Q. The word ‘Rational’ is made from the word ‘Ratio’ and rational numbers are denoted by Q because of the word ‘Quotient’.

Some Statements Related to Numbers

1. Every natural number is a whole number but every whole number is not a natural number. Because 0 is not a natural number.

2. Every natural number or whole number or integer is a rational number but every rational number is not a natural number or whole number or integer.

3. All natural numbers are also called positive integers.

4. 1 is the smallest natural number.

5. 0 is the smallest whole number.

Note – 1) All the natural numbers, whole numbers, and integers are also rational numbers because we can write them in the form of p/q. Examples – 5/1, 4/1, 0/1, 1/1, -8/1, -3/1, etc.

2) When we represent a rational number p/q on the number line, we assume q ≠ 0 and p and q do not have any common factor other than 1. It means p and q are co-prime numbers.

3) We have already studied how to find a rational number between two rational numbers. If we have to find a rational number between rational numbers a and b, then we add a and b and divide it by 2. It means a+b/2 is the rational number between a and b. Let’s understand it with an example.

Example – Find four rational numbers between 1 and 3.

Solution – Using formula a+b/2 for 1 and 3.

Rational number between 1 and 3 = 1+3/2 = 4/2 = 2 => 1, 2, 3

Rational number between 1 and 2 = 1+2/2 = 3/2 => 1, 3/2, 2, 3

Rational number between 2 and 3 = 2+3/2 = 5/2 => 1, 3/2, 2, 5/2, 3

Now, rational number between 1 and 3/2 = (1+3/2)/2 = (2+3/2)/2 = 5/2/2 = 5/4 => 1, 5/4, 3/2, 2, 5/2, 3

Therefore, four rational numbers between 1 and 3 are 5/4, 3/2, 2, and 5/2.             Ans.

Second Method – Since we have to find four rational numbers so we write 1 and 3 as rational numbers with denominators 4+1 = 5.

i.e., 1 = 1×5/5 = 5/5 and 3 = 3×5/5 = 15/5

Rational numbers between 5/5 and 15/3 = 6/5, 7/5, 8/5, 9/5, 10/5, 11/5, 12/5, 13/5, 14/5

We have to write only four rational numbers. So, we can write any four of these rational numbers.

Therefore, four rational numbers between 1 and 3 are 6/5, 7/5, 8/5, and 9/5.            Ans.

4) With the help of the above example, we can understand that there are infinitely many rational numbers between any two rational numbers.

Irrational Numbers

In the above section, we have seen that all the numbers on the number line are rational numbers or are of the form of rational numbers. Is any number on the number line not in the form of a rational number or p/q? If yes, then how many of these types of numbers are on the number line and what are they called? There are infinitely many numbers on the number line which are not of the form of p/q. These types of numbers are called irrational numbers.

Definition – A number that cannot be written in the form of p/q, is called an irrational number, where p and q are integers and q ≠ 0. Irrational numbers are denoted by T. They can also be represented by R\Q, where R shows the real numbers and Q shows the rational numbers. The meaning of R\Q is the group of numbers except rational numbers in real numbers which are irrational numbers.

Examples – √2, √3, √5, √7, p(3.1415926535897932…….), 1.010010001…, 2.14263245…  , etc.

Note – Numbers that are written in the square root (√), are positive square root numbers.

Real Numbers

On the number line, there are rational numbers and irrational numbers. Not any number is left on the number line. On the number line, all the rational numbers and irrational numbers are real numbers.

Definition ­– The collection of all the rational numbers and irrational numbers is called real numbers. Real numbers are denoted by R. It means a real number can be either rational or irrational.

With the help of the above definition, we can say that on the number line, every real number is represented by a unique point and every point represents a unique real number.

Let’s take some examples to see how can an irrational number be represented on the number line.

Example (1) Represent √2 on the number line.

Solution – To represent √2 on the number line, we consider a square OABC, whose each side is 1 unit in length.

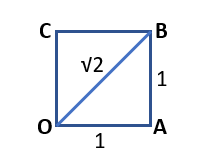
In △OAB by Pythagoras theorem,

OB² = OA² + AB²

OB² = (1)² + (1)² = 1 + 1 = 2

OB = √2

Now, we place the square OABC onto the number line but it must be ensured that vertex O coincides with zero (0).

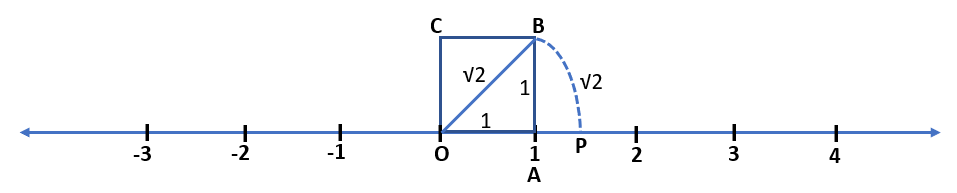
In the above figure, we can see OB = √2. With the help of a compass, taking centre O and radius OB, we draw an arc BP, which intersects the number line at the point P. This point P represents √2 on the number line.

Example 2) Represent √3 on the number line.

Solution – To represent √3 on the number line, first, we repeat the process of representing √2.

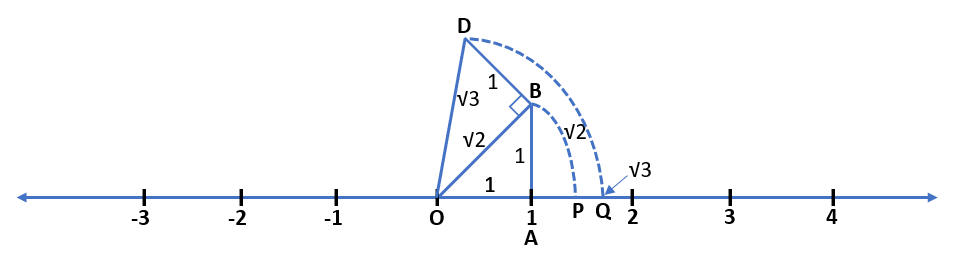
Now, we construct BD of unit length which is perpendicular to OB. After joining OD, we use Pythagoras theorem in △OBD.

OD² = OB² + BD²

OD² = (√2)² + (1)² = 2 + 1 = 3

OD = √3

Using a compass with centre O and radius OD, we draw an arc DQ, which intersects the number line at point Q. This point Q represents √3 on the number line.

Note – Similarly, we can represent √n for any positive integer n, after √(n – 1) has been represented.

Real Numbers and Their Decimal Expansions

Representing Real Numbers on the Number Line

Operations on Real Numbers

Laws of Exponents for Real Numbers

Number System Class 9^th in Hindi

More About Number System