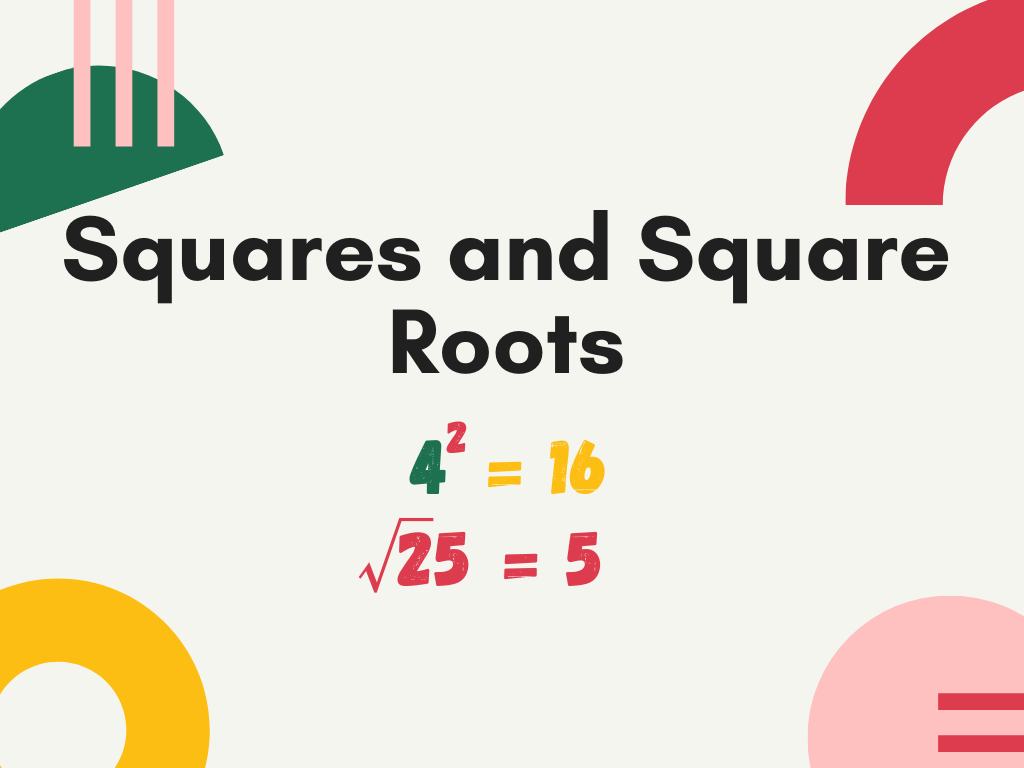Squares and Square Roots Class 8th

Introduction

In geometry, we know that a square is a figure enclosed by four equal line segments and the area of the square is given by side×side (where ‘side’ indicates the length of each side of the square). Similarly, in the number system, we find the square of the numbers with the help of this formula. In class 8th, we will study squares and square roots, properties of square numbers, methods to find the square numbers, Pythagorean triplets, square roots, and methods to find square roots, etc.

What is a Square?

To find the square of any number, we just multiply the number by itself. This process is called the Square of a number. After squaring a number, the number we get is called the Square Number.

For example –

Number	Square	Square Number
1	1×1 = (1)2	1
2	2×2 = (2)2	4
3	3×3 = (3)3	9
4	4×4 = (4)2	16
5	5×5 = (5)2	25

In the above table, 1, 4, 9, 16, and 25 are the square of 1, 2, 3, 4, and 5 respectively, and are known as square numbers. In general, we can say that if there are two natural numbers a and b, and a can be expressed as b², then a is said to be a square number. Let’s understand with examples.

Example – 1) is 36 a square number?

Solution – Yes, 36 is a square number because we can write 36 as

36 = 6×6 = 6²

Example – 2) is 46 a square number?

Solution – We know that 6² = 6×6 = 36 and 7² = 7×7 = 49.

The required number is between 6 and 7 but as we know there is not any natural number between 6 and 7. Therefore, 46 is not a square number.

Note – The square numbers are also known as perfect squares.

Properties of Square Numbers

To understand the properties of square numbers first we write squares from 1 to 30.

Number	Square	Number	Square	Number	Square
1	1	11	121	21	441
2	4	12	144	22	484
3	9	13	169	23	529
4	16	14	196	24	576
5	25	15	225	25	625
6	36	16	256	26	676
7	49	17	289	27	729
8	64	18	324	28	784
9	81	19	361	29	841
10	100	20	400	30	900

1) In the above table, we can see that unit digits (ending digits) of all the square numbers are 0, 1, 4, 5, 6, or 9. It means any number ending with digits 0, 1, 4, 5, 6, or 9 is a square number or we can say that number ending with these digits is a square of a number. The above table helps us to understand this property.

2) Now from the above table, we take the numbers having unit digits 1 or 9 and their squares.

Number	Square
1	1
9	81
11	121
19	361
21	441
29	841

From the table, we can understand that for any number having the unit digit 1 or 9, the unit digits of their squares will be always 1.

3) If we take the numbers having unit digits 4 and 6 from the table of squares given from 1 to 30. Then

Number	Square
4	16
6	36
14	196
16	256
24	576
26	676

From this table, we can understand that for any number having the unit digit 4 or 6, the unit digits of their squares will be always 6.

4) What will be the square of the numbers having unit digit 0 or ending with the number of zeroes? Let’s see with the help of some examples.

Number	Square
10	100
20	400
100	10000
300	90000
1000	1000000
4000	16000000

With the help of the above table, we can see that if a number is ending with one zero, then the square of that number will end with two zeroes. If a number is ending with two zeroes, then the square of that number will end with four zeroes and if a number is ending with three zeroes, then the square of that number will end with six zeroes.

Simply, we can say that with the square of the number, the number of zeroes is just double in the square. We can also notice one thing in the above table, squares are ending with an even number of zeroes. It means we can say that a square number can end with only an even number of zeroes.

Methods to Find Square of a Number

1. By Self Multiplication
2. By Algebraic Identity

Pythagorean Triplets

Square Roots

Methods to Find Square Root of a Number

1. Repeated Subtraction Method
2. Prime Factorization Method
3. Division Method
4. Estimation Method

Square Roots of Decimals

Squares and Square Roots Class 8th in Hindi

More About Squares and Square Roots