Perfect the Square Method Class 10th

Perfect The Square Method (Complete The Square Method)

Introduction

In the Perfect the Square Method, we convert the quadratic equation into the perfect square form and then we take the square root to obtain the required roots.

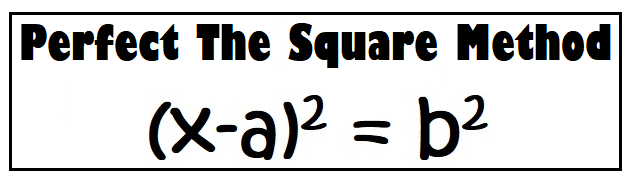
This method will be clear by the following examples.

Examples

Example – 1) Solve the quadratic equation 9x² – 3x – 2 = 0 by the perfect square method.

Solution – Given equation 9x² – 3x – 2 = 0

Step 1) We divide the whole equation by 9 to make 1 as the coefficient of x².  

9x²/9 – 3x/9 – 2/9 = 0

x² – x/3 – 2/9 = 0

Step 2) Taking the constant term to the right side

x² – x/3 = 2/9  

Step 3) Adding the square of half of the coefficient of x to both sides to make a perfect square on the left side.

x² – x/3 + (⅙)² = 2/9 + (⅙)²             [Half of coefficient of x = ⅓ ÷ 2 = ⅓⨯½ = ⅙]

Step 4) Now the left side is a perfect square.

Easy Tip – To make a perfect square, we put the sign of the middle term (– x/3) of the equation (x² – x/3 – 2/9 = 0) which in this example is – (negative), between the variable x and half of the coefficient of x which is ⅙, and make a perfect square (x – ⅙)².

(x – ⅙)² = 2/9 + 1/36

(x – ⅙)² = (2⨯4 + 1⨯1)/36 (LCM = 36)

(x – ⅙)² = 9/36

(x – ⅙)² = ¼

Step 5) By taking the square root of both sides.

√(x – ⅙)² = √¼    

x – ⅙ = ±½

Taking both values separately,

On taking the (+) sign,

x – ⅙ = +½                                            

x = ½ + ⅙                                                          

x = (1⨯3 + 1⨯1)/6                                               

x = 4/6                                               

x = ⅔                                                

On taking the (−) sign,

x – ⅙ = −½

x = −½ + ⅙

x = (−1⨯3 + 1⨯1)/6

x = −2/6

x = −⅓

So, x = ⅔ and x = −⅓ are the required roots of the quadratic equation 9x² – 3x – 2 = 0.    Ans.

Example – 2) Solve the quadratic equation 2x² – 7x + 3 = 0 by the perfect square method.

Solution – Given equation 2x² – 7x + 3 = 0

Dividing the equation by 2 to make 1 as the coefficient of x²

2x²/2 – 7x/2 + 3/2 = 0

x² – 7x/2 + 3/2 = 0

Taking the constant term to the right side

x² – 7x/2 = –3/2 

Adding the square of half of the coefficient of x to both sides   

x² – 7x/2 + (7/4)² = –3/2 + (7/4)² [Half of coefficient of x = 7/2 ÷ 2 = 7/2⨯½ = 7/4]

(x – 7/4)² = –3/2 + 49/16 = (–3⨯8 + 49⨯1)/16 = (–24 + 49)/16 = 25/16

(x – 7/4)² = 25/16  

Taking square root on both sides,

√(x – 7/4)² = √(25/16)    

x – 7/4 = ±5/4

On taking the (+) sign,

x – 7/4 = +5/4                       

x = 5/4 + 7/4                          

x = (5 + 7)/4 = 12/4                          

x = 3

On taking the (–) sign,

x – 7/4 = –5/4

x = –5/4 + 7/4

x = (–5 + 7)/4 = 2/4 

x = ½

Both the values of the x are the required roots.  Ans.

Perfect the Square Method Class 10^th in Hindi

More About Perfect the Square Method