Division Algorithm, Remainder Theorem, and Factor Theorem Class 10th

Introduction

Division Algorithm, Remainder Theorem, and Factor Theorem all three are related to Algebra. These three represent the relationship between the two functions.

Division Algorithm

If p(x) and g(x) are two such polynomials that the degree of p(x) is greater than g(x) and g(x) ≠ 0, and we divide p(x) by g(x) then we get two polynomials as quotient q(x) and remainder r(x) such that

p(x) = g(x).q(x) + r(x)

Where r(x) = 0 or the degree of the r(x) is smaller than g(x).

Example – Divide the polynomial p(x) = 2x⁴ – 3x³ + 3x + 1 by x + 1.

Solution –

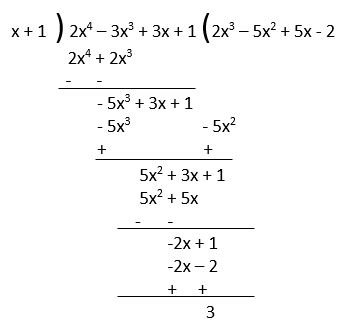
Quotient = 2x³ – 5x² + 5x – 2     Remainder = 3

Steps –

1. First of all, we arrange the dividend and divisor in descending order if they are not arranged.in this question, both are arranged in descending order.
2. Then we divide the first term of the dividend by the first term of the divisor. We divide 2x⁴ by x and get 2x³. This is the first term of quotient.
3. We multiply the divisor (x+1) by the first term of the quotient 2x³ and subtract the product 2x⁴ + 2x³ from the dividend. this gives the remainder -5x³ +3x + 1.
4. This remainder -5x³ + 3x + 1 is our new dividend. we repeat step (2) to get the second term of the quotient as – 5x².
5. Similarly, like step (3) we multiply the second term of the quotient – 5x² by the divisor (x+1) and subtract the product – 5x³ – 5x² from the new dividend. We write the like term below the like term and if there is any unlike term then we write that term separately.

This process continues till the remainder is 0 or the degree of the new dividend is less than the degree of the divisor. At the last, the new dividend will be the remainder. 

Here, zero of divisor x + 1 is x + 1 = 0 ⇒ x = -1

So, p(x) at x = -1,   p(-1) = 2(-1)⁴ – 3(-1)³ + 3(-1) + 1

p(-1) = 2 – 3(-1) – 3 + 1

p(-1) = 2 + 3 – 3 + 1 = 3 (Remainder)

It means we can find the remainder r(x) of any division by putting the value of the zero of divisor g(x) in dividend p(x).

Remainder Theorem

Let p(x) be any polynomial of degree one or greater than one and let a be any real number. If p(x) is divided by the linear polynomial (x – a), then the remainder is p(a).

Example – find the remainder when x⁴ – 4x² + x³ + 2x + 1 is divided by x – 1.

Solution – let p(x) = x⁴ – 4x² + x³ + 2x + 1

Zero of x – 1 is x – 1 = 0 ⇒ x = 1

So, p(x) at x = 1,   p(1) = (1)⁴ – 4(1)² + (1)³ + 2(1) + 1

p(1) = 1 – 4 + 1 + 2 + 1 = 1      

Therefore, Remainder is 1.              Ans.

Factor Theorem

If polynomial p(x) is divided by polynomial g(x) with remainder r(x) = 0 then the polynomial g(x) will be one factor of polynomial p(x) or we can say if g(x) is one factor of p(x) then the remainder r(x) will be zero.

Example – Examine whether x – 3 is a factor of polynomial x³ – 3x² + 4x – 12.

Solution – let p(x) = x³ – 3x² + 4x – 12 

We know if (x – 3) is a factor of p(x) then the remainder will be 0.

the zero of x – 3 is x – 3 = 0 ⇒ x = 3

Now p(x) at x = 3,    p(3) =  (3)³ – 3(3)² + 4(3) – 12      

p(3) =  27 – 3(9) + 12 – 12

p(3) = 27 – 27 + 12 – 12 = 0

∵ The remainder is 0 so (x – 3) is the factor of polynomial p(x).       Ans.

Note – Here, zero is x = 3 so the factor is x – 3. We can find the factor if we know the zero and we can find the zero if we know the factor of any polynomial.

Division Algorithm, Remainder Theorem, and Factor Theorem Class 10^th in Hindi

More About Division Algorithm, Remainder Theorem, and Factor Theorem