Linear Equations in Two Variables Class 9th

• A linear equation having two variables is called a linear equation in two variables. Example – (1) 2x + 3y = 8 (2) a – 4b + 3 = 0 (3) 5u – v – 2 = 0
• An equation having degree (highest power of the variable) one is called a linear equation.

Standard Form of Linear Equations in Two Variables

• The standard form of linear equations in two variables is given as follows:

ax + by + c = 0

• Where a, b, and c are real numbers and a, b ≠ 0.
• We can also say that the equation which can be put in the form of ax + by + c = 0 is called a linear equation in two variables.

Example – Write each of the following equations in the form ax + by + c = 0 and indicates the values of a, b, and c in each case:

(i) 3x + 4y = 7      (ii) x – 5 = 2y      (iii) 8 = y – 9x      (iv) 10x = y      (v) y = 1      (vi) 3 – 4x = 0

Solution – (i) 3x + 4y = 7

We can write 3x + 4y – 7 = 0. Here, a = 3, b = 4 and c = -7

(ii) x – 5 = 2y

We can write x – 2y – 5 = 0. Here, a = 1, b = -2 and c = -5

(iii) 8 = y – 9x

We can write 9x – y + 8 = 0. Here, a = 9, b = -1 and c = 8

(iv) 10x = y

We can write 10x – y + 0 = 0. Here, a = 10, b = -1 and c = 0

(v) y = 1

We can write 0.x + y – 1 = 0. Here, a = 0, b = 1 and c = -1

(vi) 3 – 4x = 0

We can write -4x + 0.y + 3 = 0. Here, a = -4, b = 0 and c = 3

Solution of a Linear Equation in two Variables

• In a linear equation in two variables, we know that there are two variables.
• Therefore, the solution will be in the form of a pair of values, one for x and one for y.
• Both the values of x and y satisfy the given equation.

Let’s take an example to understand it.

Example – x + 2y = 8

If we substitute x = 0 and y = 4 in the above equation then we get

0 + 2×4 = 8

8 = 8

LHS = RHS

Therefore, x = 0 and y = 4 is a solution of this equation. We can also write it in the form of a pair (0, 4). In the pair, the first value is for x and the second value is for y.

If we substitute x = 1 and y = 2 in the above equation then we get

1 + 2×2 = 8

1 + 4 = 8

5 ≠ 8

LHS ≠ RHS

Therefore, x = 1 and y = 2 is not a solution of this equation.

Similarly, (8, 0) and (4, 2) are also the solutions of the above equation.

We can also find the solution of a linear equation in two variables by substituting any value of our choice for x or y. let’s take another equation 3x – y = 5.

If we substitute x = 2 in the given equation then we get

3×2 – y = 5

The equation reduces into one variable y which is a linear equation in one variable. Now we can easily solve this equation.

6 – y = 5

6 – 5 = y

y = 1

Therefore, (2, 1) is a solution of equation 3x – y = 5.

Similarly, for y = 0, we get x = 5/3. So, (5/3, 0) is another solution to this equation.

Note – With the help of the above explanation, we can say that a linear equation in two variables has infinitely many solutions.

Example – Find four different solutions of equation 4x + y = 1.

Solution – 4x + y = 1

(i) For x = 0

4×0 + y = 1

y = 1

So, (0, 1) is a solution of the given equation.

(ii) For x = 1

4×1 + y = 1

4 + y = 1

y = 1 – 4

y = -3

So, (1, -3) is another solution to the given equation.

(iii) For y = 5

4x + 5 = 1

4x = 1 – 5

4x = -4

x = -4/4

x = -1

So, (-1, 5) is a solution of the given equation.

(iv) For y = 0

4x + 0 = 1

4x = 1

x = ¼

So, (1/4, 0) is a solution of the given equation.                                   Ans.

Graph of Linear Equations in Two Variables

• To represent a linear equation in two variables graphically, we find some values of y or x which correspond to values of x or y.
• We make a table for the values of x and y.
• Let us understand this with the help of an example.

Example – Represent the equation x + 3y = 5 graphically.

Solution – First, we find the values of x corresponding to the values of y.

x + 3y = 5

We can also write like this, x = 5 – 3y

x	5	2	-1	8
y	0	1	2	-1

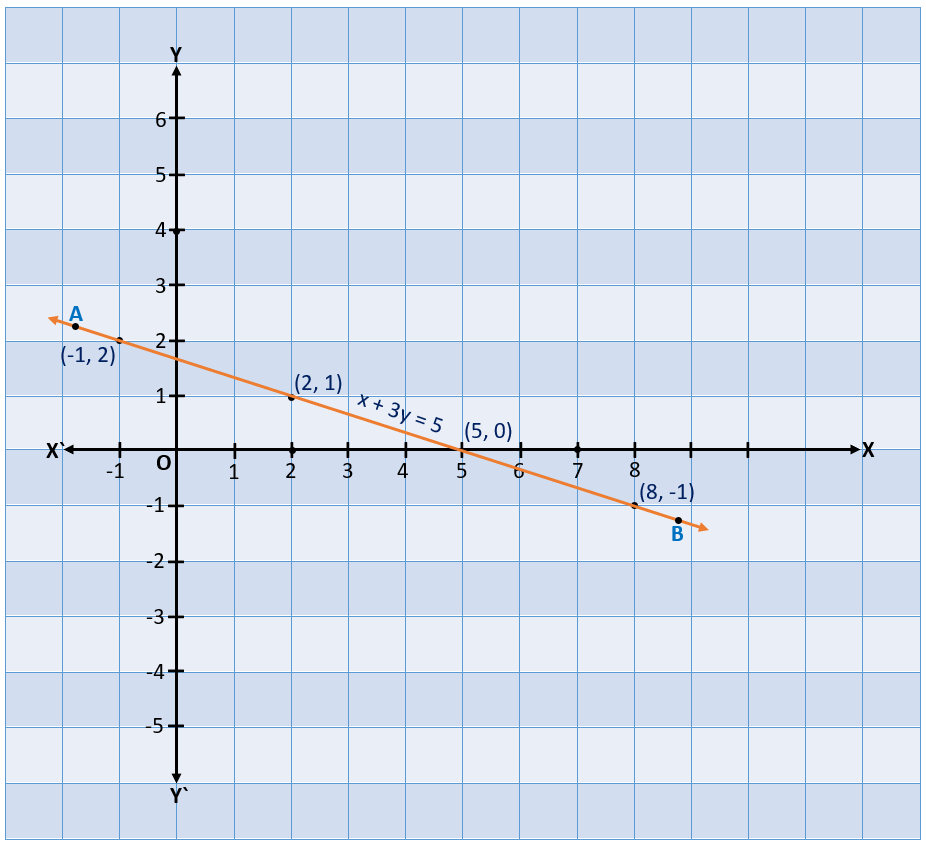
• After finding the values of x and y, we plot the points on graph paper and by joining them we get a straight-line AB.
• We can see that all the points lie on the straight-line AB. If we find more points they will lie on the line AB or not?
• As shown above, if we find a point and the point is a solution of the given equation then it will lie on line AB and if not a solution then it will not lie on line AB.
• We can conclude that every point on the line satisfies the equation of the line and every solution of the equation is a point on the line.

Note – 1) Every point whose coordinates satisfy the equation lies on the line.

2) Every point (a, b) on the line gives a solution x = a and y = b of the equation.

3) Any point, which is not a solution of an equation, does not lie on the line of that equation and any point, which does not lie on the line, is not a solution of that equation.

4) The equation having degree one is called a linear equation and the graph of the linear equation is a straight line.

Equations of Lines Parallel to the x-axis and y-axis

• In coordinate geometry, the points (2, 0), (-1, 0), and (4, 0) lie on the x-axis because the y-coordinates of the points are zero.
• Similarly, the points (0, -2), (0, 1), (0, -4) lie on the y-axis because the x-coordinates of the points are zero.
• The equation of the x-axis is given by y = 0 and the equation of the y-axis is given by x = 0.  
• We have seen some linear equations in two variables like x = 3, 2x + 5 = 0, y – 2 = 0, 2y = -7, etc.

If we write these equations properly

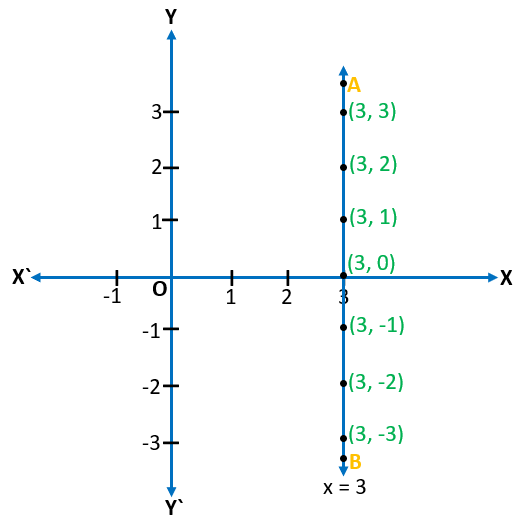
x = 3 or x + 0.y = 3

2x + 5 = 0 or 2x + 0.y + 5 = 0

y – 2 = 0 or 0.x + y – 2 = 0

2y = -7 or 0.x + 2y = -7

• In all the above equations, there is only one variable, and if we find the value of that variable for different values of another variable that is directly not present in the equation. Then

x = 3 or x + 0.y = 3

x = 3 for y = 0, 1, 2, 3, 4……….

• It means (3, 0), (3, 1), (3, 2), (3, 3), (3, 4) ……. are the solutions of this equation. We can see that the value of x is 3 in every solution. It means the line of this equation will pass through the point x = 3.
• In this graph, the straight line will be parallel to the y-axis.

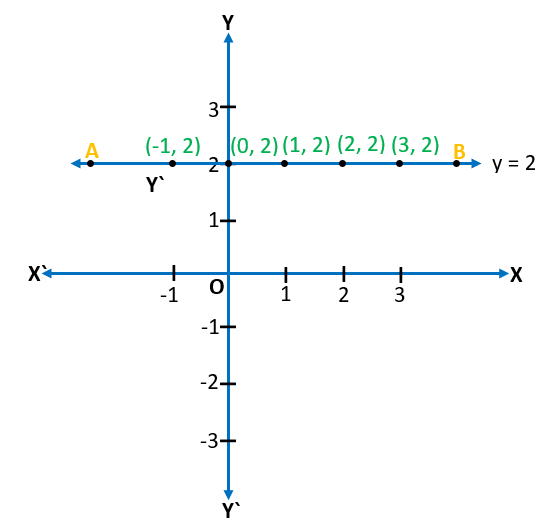
• Similarly, for y – 2 = 0 or 0.x + y – 2 = 0, the line of this equation will pass through the point y = 2, and the graph (straight line) will be parallel to the x-axis.

Graph for x = 3 or x + 0.y = 3 which is parallel to the y-axis.

Graph for y – 2 = 0 or 0.x + y – 2 = 0 or y = 2 which is parallel to the x-axis.

Linear Equations in two Variables Class 9th in Hindi

More About Linear Equations in Two Variables