Decimal Expansion of Rational Numbers Class 10th

1 Comment / Number System, Number System Class 10th / By / a number whose decimal expansion is terminating or non terminating recurring is, decimal expansion of a rational number, decimal expansion of a rational number cannot be, decimal expansion of a rational number is terminating, decimal expansion of a rational number is terminating if in its denominator there is, decimal expansion of rational and irrational numbers, decimal expansion of rational number is terminating, decimal expansion of rational numbers, decimal expansion of real numbers, examples of non terminating decimal expansion, if the decimal representation of a number is non terminating non repeating then the number is, mitacademys.com, numbers have either terminating or non terminating repeating decimal expansion, numbers having non terminating non repeating decimal expansion are known as, rational numbers and their decimal expansions, rational numbers decimal expansion, real numbers and decimal expansions, real numbers and their decimal expansion, real numbers decimal expansion, repeating decimal expansion, revisiting rational numbers and their decimal expansions, terminating and non terminating decimal expansion, terminating and nonterminating decimals, terminating decimal expansion, the decimal expansion of a rational number, the decimal expansion of a rational number may be, the decimal expansion of an rational number is, the decimal expansion of the rational number, the decimal expansion of the rational number will terminate after, the following real numbers have decimal expansion, the following real numbers have decimal expansions as given below, the number of decimal places after which the decimal expansion of the rational number, what is terminating and non terminating decimal expansion, which of the following has a terminating decimal expansion, which of the following has terminating decimal expansion, which of the following have terminating decimal expansion, which of the following is terminating decimal expansion, which of the following numbers has terminating decimal expansion, which of the following numbers have the non terminating repeating decimal expansion, which of the following rational number have non terminating and repeating decimal expansion, which of the following rational number have non terminating repeating decimal expansion, which of the following rational number will have a terminating decimal expansion, which of the following rational numbers has a terminating decimal expansion, which of the following rational numbers has terminating decimal expansion, which of the following rational numbers have a terminating decimal expansion, which of the following rational numbers have non terminating repeating decimal expansion, which of the following rational numbers have terminating decimal expansion, which one of the following rational number has non terminating decimal expansion, which one of the following rational number is a non terminating decimal expansion

Introduction

We have already studied that the number which can be written in the form of p/q is called a Rational Number. Where p and q are integers and q ≠ 0. The decimal expansion of rational numbers is either a terminating decimal expansion or a non-terminating repeating (recurring) decimal expansion. In this section, we shall study and explore exactly when a rational number has the terminating decimal expansion and when it is a non-terminating repeating (recurring) decimal expansion. Let us understand with the help of several examples.

DECIMAL EXPANSION OF RATIONAL NUMBERS

Explanation

Let us consider some rational numbers-

1) 3.75         2) 0.540         3) 14.2680              4) 0.0963              5) 123.2

After converting these numbers, we get

1) 3.75 = 375/100 = 375/102

2) 0.540 = 540/1000 = 54/100 = 54/102

3) 14.2680 = 142680/10000 = 14268/1000 = 14268/103

4) 0.0963 = 963/10000 = 963/104

5) 123.2 = 1232/10

In the above examples, the denominator of all rational numbers is in the form of a power of 10. If we solve these rational numbers further and factorize the numerator and cancel the common factor in the numerator and denominator then let’s see what we get.

1) 3.75 = 375/102 = 3×53/(2×5)2 = 3×53/22×52 = 3×5/22

2) 0.540 = 54/102 = 2×33/(2×5)2 = 2×33/22×52 = 33/2×52

3) 14.2680 = 14268/103 = 22×3×29×41/(2×5)3 = 22×3×29×41/23×53 = 3×29×41/2×53

4) 0.0963 = 963/104 = 32×107/(2×5)4 = 32×107/24×54

5) 123.2 = 1232/10 = 24×7×11/2×5 = 23×7×11/5

In the above examples, one thing is common in the denominators of all the rational numbers. What is that let’s determine,

In example 1), Rational number = 3×5/22, Denominator = 22 or we can write 22×50  [∵ 50= 1]

In example 2), Rational number = 33/2×52, Denominator = 21×52

In example 3), Rational number = 3×29×41/2×53, Denominator = 21×53

In example 4), Rational number = 32×107/24×54, Denominator = 24×54

In example 5), Rational number = 23×7×11/5, Denominator = 5 or we can write 20×51

In all the Rational numbers, the common thing is that their Denominators are in the form of powers of 2 or powers of 5 or both. We know that the prime factors of 10 are 2×5 so powers of 10 can have only powers of 2 and 5 as factors. Because of powers of 10 in the Denominators of all the Rational numbers, we get the factors in the form of powers of 2 or powers of 5, or both.

If we take more examples whose decimal expansions are terminating decimal expansions those numbers can be expressed in the Rational numbers whose Denominators are in the powers of 2 or 5 or in the powers of 10. After canceling out the common factors in the numerator and denominator of rational numbers, we shall find that the Denominator of the Rational number is in the form of 2n×5m, where n and m are the non-negative integers.

We can write the result of the above examples in the form of the following theorem.

Theorem 1) If x is a rational number whose decimal expansion is terminating, then x can be expressed in the form of p/q, where p and q are coprime numbers and the prime factorization of q is of the form 2n×5m where n and m are non-negative integers.

The converse of the theorem is also true. Let us see with the help of the above examples.

We shall solve the above examples in reverse order.

1) 3×5/22 = 15/22 = 15×52/22×52 (On multiplying the numerator and denominator by 52)

= 15×25/(2×5)2 = 375/(10)2 = 375/100 = 3.75

2) 33/2×52 = 27/2×52 = 27×2/2×2×52 (On multiplying the numerator and denominator by 2)

= 54/22×52 = 54/(2×5)2 = 54/(10)2 = 54/100 = 0.54 or 0.540

3) 3×29×41/2×53 = 3567/2×53 = 3567×22/2×53×22 (On multiplying the numerator and denominator by 22)

= 3567×4/23×53 = 14268/(2×5)3 = 14268/(10)3 = 14268/1000 = 14.268 or 14.2680

4) 32×107/24×54 = 963/(2×5)4 = 963/(10)4 = 963/10000 = 0.0963 (the denominator is already in the power of 10)

5) 23×7×11/5 = 616/5 = 616×2/5×2 (On multiplying the numerator and denominator by 2)

= 1232/10 = 123.2

From the above examples, we can say that we can convert a rational number of the form p/q (where q is of form 2n×5m) into an equivalent rational number whose denominator is in the power of 10. So, the decimal expansion of these types of rational numbers is terminating decimal expansion. We can write this result as the theorem given below.

Theorem 2) If x is a rational number of the form p/q, such that prime factorization of q is of the form 2n×5m where n and m are non-negative integers then decimal expansion of x is terminating decimal expansion.

Now we consider the rational numbers whose denominators are not in the form of power of 10 or in the form of 2n×5m. Decimal expansion of these types of rational numbers is non-terminating repeating decimal expansion.

Let us consider some of these rational numbers.

1) 1/3                   2) 300/37               3) 47/99                   4) 7/6

Here, Denominators of all the rational numbers are not in the form of 2n×5m so we shall divide the numerator by Denominator to get the decimal expansion.

1) 1/3

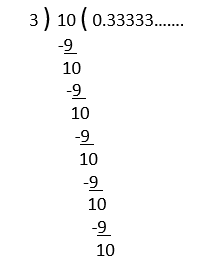
DECIMAL EXPANSION OF RATIONAL NUMBERS

2) 300/37

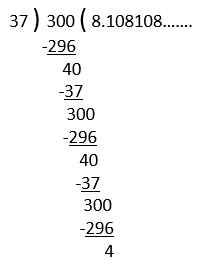
3) 47/99

DECIMAL EXPANSION OF RATIONAL NUMBERS

4) 7/6

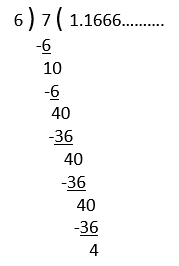
After dividing each rational number, we do not obtain Remainder 0 and the division process is not terminating and the digits are repeating in the quotient, therefore, the decimal expansion of all the above rational numbers will be non-terminating repeating (recurring).

It means we can say that the rational numbers whose denominators are not in the form of 2n×5m have non-terminating repeating decimal expansion. We can write this result in the form of a theorem.

Theorem 3) If x is a rational number of the form p/q, such that prime factorization of q is not of the form 2n×5m where n and m are non-negative integers then decimal expansion of x is non-terminating repeating (recurring) decimal expansion.

Note – 1) The above explanations show that the Decimal expansion of every Rational number is either terminating or non-terminating repeating (recurring).

2) If there is a number whose decimal expansion is non-terminating non-repeating then the number is called Irrational Number.

Some Examples

Example 1) Without actually performing the long division method, write the Decimal expansion of 17/3125 and 77/210.

Solution – Here, 17/3125 = 17/20×55

Denominator 3125 is of the form 2n×5m, so 17/3125 has a terminating decimal expansion.

Now 77/210 = 77/2×3×5×7   

Denominator 210 is not of the form 2n×5m, so 77/210 has a non-terminating repeating decimal expansion.          Ans.

Example 2) With the help of decimal expansion, decide whether the given numbers are Rational numbers or Irrational numbers.

i) 123.1236289476…….      ii) 34.654321             iii) 0.324532453245………..

Solution – i) 123.1236289476…….

The Decimal expansion of this number is non-terminating non-repeating so this number is an Irrational number.

ii) 34.654321

The Decimal expansion of this number is terminating so this number is a Rational number.

iii) 0.324532453245………..

The Decimal expansion of this number is non-terminating repeating so this number is a Rational number.          Ans.

Decimal Expansion of Rational Numbers Class 10th in Hindi

More About Decimal Expansion of Rational Numbers

Rate this post

Related posts

Decimal Expansions of Real Numbers Class 9th Operations on Real Numbers Class 9th Decimal Numbers Class 7th Number System Class 9th Rational Numbers Class 8th Representation of Real Numbers on the Number Line Class 9th Irrational Numbers and Irrationality Class 10th परिमेय संख्याओं का दशमलव प्रसार कक्षा 10 (Decimal Expansion of Rational Number Class 10th) Real Numbers Class 8th वास्तविक संख्याओं का दशमलव प्रसार कक्षा 9वीं (Decimal Expansion of Real Numbers Class 9th) Fractions Class 7th Whole Numbers Class 6th Polynomials Class 10th About Libre office. Microsoft office 2016About Microsoft office 2016 Powers and Exponents Class 8th संख्या रेखा पर वास्तविक संख्याओं का निरूपण कक्षा 9वीं (Representation of Real Numbers on the Number Line Class 9th) Sets Class 11th Apache open officeApache Open Office. परिमेय संख्याएँ कक्षा 8 (Rational Numbers Class 8th) About Microsoft Office 2013 Pro Plus. Relations and Functions Class 12th Laws of Exponents for Real Numbers Class 9th घात और घातांक कक्षा 8 (Powers and Exponents Class 8th) The Fundamental Theorem of Arithmetic Class 10th बहुपद कक्षा 10 (Polynomial Class 10th) Circumference of Circle Class 10th Integers Class 6th Arithmetic Progression Class 10th Areas Related to Circles Class 10th संख्या पद्धति कक्षा 9वीं (Number System Class 9th) Everything About Microsoft Windows 10. Trigonometry Class 10th About Microsoft Office 2013 Pro Plus Hindi. दशमलव संख्याएँ कक्षा 7 (Decimal Number Class 7th) nth Term (General Term) of an Arithmetic Progression Class 10th वास्तविक संख्याओं पर संक्रियाएँ कक्षा 9वीं (Operations on Real Numbers Class 9th) learn c programmingLearn C Programming त्रिकोणमिति कक्षा 10 (The Trigonometry Class 10th) microsoft office 2016About Microsoft office 2016 Hindi About Raspberry pi board javascript programmingLearn Java Script Programming Coordinate Geometry (Analytical Geometry) Class 10th mysqlAbout mysql Libre office 5About Libre office In Hindi. html5Learn Html5 Computer Fundamental. निर्देशांक ज्यामिति कक्षा 10 (The Coordinate Geometry Class 10th) Quadratic Equation Class 10th Everything About Microsoft Windows 10.Everything About Microsoft Windows 10 Hindi. Polynomials Class 9th Operations on Polynomials Class 10th reactjsAbout ReactJs Framework bootstrap cssWhat Is Bootstrap Css tailwind cssWhat Is Tailwind Css view.jsAbout Vue.js tableauAbout Python Tableau htmlLearn Html समान्तर श्रेढ़ी कक्षा 10 (Arithmetic Progressions Class 10th) वास्तविक संख्याओं के लिए घातांक के नियम कक्षा 9 (Laws of Exponents for Real Numbers Class 9th) समान्तर श्रेढ़ी का n वाँ पद (व्यापक पद) कक्षा 10 (nth Term of Arithmetic Progression Class 10th) bulma cssWhat Is Bulma Css Windows legacy osMicrosoft Windows Legacy Operating system. Lines and Angles Class 9th python numpyAbout Python Numpy scipy python libraryAbout Scipy Python Library ncert class 10th math solutionNCERT Maths Class 10th Solution Euclid’s Division Lemma Class 10th Coordinate Geometry Class 9th Geometrical (Graphical) Meaning of the Zeroes of a Polynomial Class 10th द्विघात समीकरण कक्षा 10 (Quadratic Equations Class 10th) plsqlAbout Pl/Sql javaLearn Java Programming arduinoAbout Arduino Microcontroller Board nodejsWhat is Nodejs अपरिमेय संख्या और अपरिमेयता कक्षा 10 (Irrational Number and Irrationality Class 10th) xmlAbout Xml mongodbAbout MongoDb Database Sum of First n Terms of an Arithmetic Progression Class 10th Squares and Square Roots Class 8th scala programmingAbout Scala Programming Triangle and its Properties Class 10th त्रिभुज और इसके गुण कक्षा 10 (The Triangle and its Properties Class 10th) बहुपद के शून्यकों का ज्यामितीय (आलेखीय) अर्थ कक्षा 10 [Geometrical (Graphical) Meaning of the Zeroes of the Polynomial Class 10th] Heron’s Formula Class 9th magentoAbout Magento Programming Pair of Linear Equations in Two Variables Class 10th दो चरों वाले रैखिक समीकरण कक्षा 9 (Linear Equations of two Variables Class 9th) Probability Class 10th Linear Equations in Two Variables Class 9th हीरोन का सूत्र कक्षा 9 (Heron’s Formula Class 9th) वृत्त की परिधि कक्षा 10 (The Circumference of Circle Class 10th) Windows 10 apps DescriptionMicrosoft Windows 10 Operating System Apps. समान्तर श्रेढ़ी के पहले n पदों का योग कक्षा 10 (Sum of n Terms of Arithmetic Progression Class 10th) Windows 7About Microsoft Windows 7. postgresqlAbout Postgresql pandasAbout Pandas Perimeter and Area Class 6th Section Formula Class 10th Apache open office hindiApache Open Office Hindi. परिमाप और क्षेत्रफल कक्षा 6 (Perimeter and Area for Class 6th) समुच्चय कक्षा 11 (The Sets Class 11th) expressjsWhat Is Express.js वृत्तों से संबंधित क्षेत्रफल कक्षा 10 (Areas Related to Circle Class 10th) Introduction to Euclid’s Geometry Class 9th Variance in Statistics: Definition, Formulas, Properties, and Examples विभाजन सूत्र कक्षा 10 (The Section Formula Class 10th) Tangent and Secant of Circle Class 10th वृत्त की स्पर्श रेखा और छेदक रेखा कक्षा 10 (Tangent and Secant of Circles Class 10th) About Microsoft office 365. Windows 7 hindiAbout Microsoft Windows 7 Hindi. What is linuxLinux, What is Linux, A Complete Overview of Ubuntu Linux. InternetWhat Is The Internet? पूर्ण संख्याएँ कक्षा 6 (Whole Number Class 6th) Area of Triangle in Coordinate Geometry Class 10th यूक्लिड की ज्यामिति का परिचय कक्षा 9 (Introduction to Euclid’s Geometry Class 9th) Distance Between Two Points in Cartesian Plane and Distance Formula Class 10th kotlinAbout Kotlin Programming निर्देशांक ज्यामिति कक्षा 9 (The Coordinate Geometry Class 9th) Data type in c programmingData Type In C Programming. c# programmingAbout C# Programming jsonAbout Json json javascript object notation पूर्णांक संख्याएँ कक्षा 6 (Integer Class 6th) कार्तीय समतल में दो बिन्दुओं के बीच की दूरी और दूरी सूत्र कक्षा 10 (The Distance Formula Class 10th) Angle Subtended by a Chord of Circle Class 10th वृत्त की जीवा द्वारा अंतरित कोण कक्षा 10 (Angle Made by a Chord of Circle Class 10th) बहुपदों पर संक्रियाएँ कक्षा 10 (Operation on Polynomial Class 10th) दो चर वाले रैखिक समीकरण युग्म कक्षा 10 (Pair of Linear Equations in Two Variables Class 10th) रेखाएँ और कोण कक्षा 9 (Lines and Angles Class 9th) वास्तविक संख्याएँ कक्षा 8 (Real Number Class 8th) Windows 8.1 appsMicrosoft Windows 8 Apps. Windows 10 Apps HindiMicrosoft Windows 10 Apps Hindi. sql dbmsAbout Sql – Structure Query Language search engineWhat Is A Search Engine and Their Type? Linear Equations in One Variable Class 8th Windows operating systemMicrosoft Windows Legacy Operating System Hindi. बहुपद कक्षा 9वीं (Polynomial Class 9th) HTML ElementsHTML Elements joomlaAbout Joomla Cms NCERT गणित कक्षा 10 अध्याय 1 वास्तविक संख्याएँ हल Angle Subtended by the Arc of a Circle Class 10th Cyclic Quadrilaterals Class 10th angularjsWhat is Angular Js भिन्न संख्याएँ कक्षा 7 (Fraction Class 7th) An In-Depth Review of imagestotext.io in 2023 asp.netAbout Asp.net Integers Class 7th एक वृत्त के चाप द्वारा अंतरित कोण कक्षा 10 (Angles Made by the Arc of Circle Class 10th) चक्रीय चतुर्भुज कक्षा 10 (Cyclic Quadrilateral Class 10th) अंकगणित की आधारभूत प्रमेय कक्षा 10 (Fundamental Theorem of Arithmetic Class 10th)

Similar Posts

1 thought on “Decimal Expansion of Rational Numbers Class 10th”

Leave a Comment

Your email address will not be published. Required fields are marked *

Scroll to Top