Angle Subtended by the Arc of a Circle Class 10th

Introduction

We studied the chords in a circle. We take the endpoints of the chord which are on the circle and the circular length of both endpoints is called an Arc. If there are two equal arcs then the angle subtended by both the arcs at the Centre will be equal and if there are two congruent circles then the angle made by two equal arcs will be equal. This can be better understood by the drawn figures.

Explanation

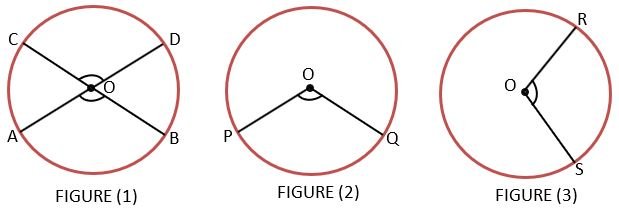
In figure (1), there are two equal arcs AB and CD and the angles made by both the arcs at the Centre of the circle are ∠AOB and ∠COD. Both angles will be equal because of equal arcs.

In figure (2) and figure (3), there are two congruent circles with Centre O. In both circles, there are two equal arcs PQ and RS. Angles made by both the arcs are ∠POQ and ∠ROS. Both angles will be equal because of equal arcs in congruent circles.

Note – 1) In the above figures, if we take chords corresponding to their arcs then angles subtended by chords will be also equal.

2) In a circle, the minor arc subtends the acute angle at the Centre and the major arc subtends the reflex angle at the Centre.

What happens when an angle is subtended by an arc at the Centre of the circle and an angle is subtended by the same arc on the same circle? Let’s see

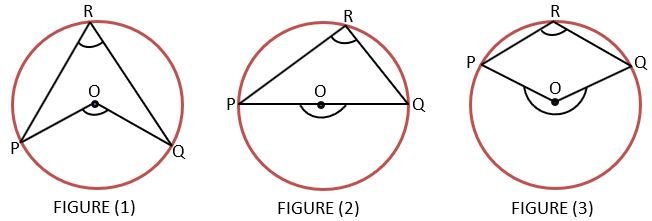
In the above figures, if we measure each angle in each circle then we will find that

In figure 1) ∠POQ = 120° and ∠PRQ = 60°

In figure 2) ∠POQ = 180° and ∠PRQ = 90°

In figure 3) ∠POQ = 240° and ∠PRQ = 120°

From the above observation, we found that in all three circles angle subtended by arc PQ at the Centre is double the angle subtended by the same arc PQ on the circle. It shows that the angle made by an arc at the Centre is two times the angle made by the same arc at any point of the circle. We can prove this with the help of the theorem. Here we are proving the theorem for figure (1).

Theorems Based on it

Theorem 1) The angle subtended by an arc at the Centre is double the angle subtended by it at any point on the remaining part of the circle.

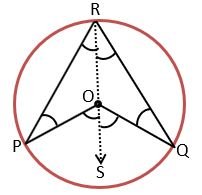
Given – Arc PQ subtend ∠POQ at Centre and ∠PRQ at point R on the circle.

Prove that – ∠POQ = 2∠PRQ

Construction – Joined point R to Centre O and extend it to point S.

Proof – By exterior angle property in △POR

∠POS = ∠PRO + ∠OPR ————(1)

∵ OR = OP (Radii of the same circle)

∴ ∠PRO = ∠OPR (Opposite angles of equal sides are equal)

From equation (1)

∠POS = ∠PRO + ∠PRO

∠POS = 2∠PRO —————(2)

Similarly in △QOR,

∠QOS = 2∠QRO —————(3)

By adding equations (2) and (3)

∠POS + ∠QOS = 2∠PRO + 2∠QRO

∠POQ = 2(∠PRO + ∠QRO)

∠POQ = 2∠PRQ                Hence Proved.

Note – This theorem can also be proved for figure (2) and figure (3).

In figure (2), ∠POQ = 180° (angle on diameter)

So, ∠PRQ = 90°

It shows that an angle made in a semicircle is always a right angle or we can say that a semicircle subtends a right angle.

In the above theorem, point R is taken on the circle. If we take another point S on the same circle then there will be subtended two angles on the circle.

What will be the relation between them, Let’s understand by the theorem.

Theorem – 2) angles subtended by an arc in the same segment are equal.

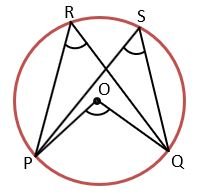
Given – angles ∠PRQ and ∠PSQ are subtended by arc PQ on the circle.

Prove that – ∠PRQ = ∠PSQ

Proof – In the figure, there are two angles subtended on the circle by the arc PQ.

By theorem (1), ∠POQ = 2∠PRQ and ∠POQ = 2∠PSQ

Therefore, 2∠PRQ = 2∠PSQ

∠PRQ = ∠PSQ

This relation shows that the angles subtended by an arc in the same segment are always equal.     Hence Proved.

Converse of Theorem

Theorem 3) – If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, then the four points lie on a circle.

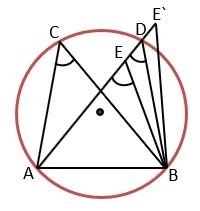
Given – AB is chord and ∠ACB = ∠ADB

Prove that – Points A, B, C and D lie on the circle.

Proof – ∠ACB = ∠ADB (given)

Let us consider that the circle is passing through points A, B, and C. it does not pass through point D. it means the circle will intersect line AD at E or intersect extended AD at E`.

If points A, C, E and B lie on the circle then,

∠ACB = ∠AEB (angles made in the same segment by an arc are equal)

But ∠ACB = ∠ADB (given)

Therefore, ∠AEB = ∠ADB

It means points E and D coincide with each other.

Similarly, E` will also coincide with D.

So, it is proved that points A, B, C and D lie on a circle.             Hence Proved.

Some Examples –

Example 1) In the figure, ∠AOB = 84°. Find the ∠ACB.

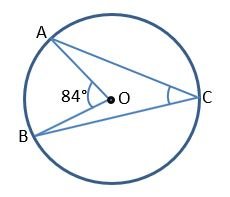
Solution – According to the theorem, the angle made on the Centre of the circle is double the angle made on the circle. So,

∠AOB = 2∠ACB

84° = 2∠ACB                [given ∠AOB = 84°]

84°/2 = ∠ACB

42° = ∠ACB

Therefore, ∠ACB = 42°                Ans.

Example 2) In the figure, angles made by chords PQ and PR on the Centre of the circle are 76° and 130°. Find the value of ∠QPR and ∠QOR.

Solution – Given ∠POQ = 76° and ∠POR = 130°

∠QOR = 360° – (76° + 130°)   [angle made on the Centre of the circle is 360°]

∠QOR = 360° – (206°)

∠QOR = 154°

∠QPR = ½(∠QOR)   [angle made on the Centre of the circle is double the angle made on the circle]

∠QPR = ½⨯(154°) = 77°

∠QPR = 77°            Ans.

Example 3) In the given figure, find the ∠PSQ if ∠POQ = 100°.

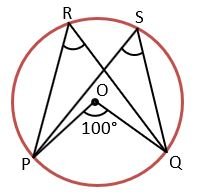
Solution – Given ∠POQ = 100°

So, ∠PRQ = ½(∠POQ) [angle made on the Centre of the circle is double the angle made on the circle]

∠PRQ = ½⨯(100°)

∠PRQ = 50°

Since ∠PRQ = ∠PSQ [angles made by an arc in the same segment are equal]

Therefore,   ∠PSQ = 50°                   Ans.

Some Short Type Questions

Q 1) What is the Arc?

Ans. – The circular length of the two points situated on the circle is called an Arc.

Q 2) What is the measure of the angle subtended by the diameter on the circle?

Ans. – Right angle (90°)

Angle Subtended by the Arc of a Circle Class 10^th in Hindi

More About Angle Subtended by the Arc of a Circle