Introduction
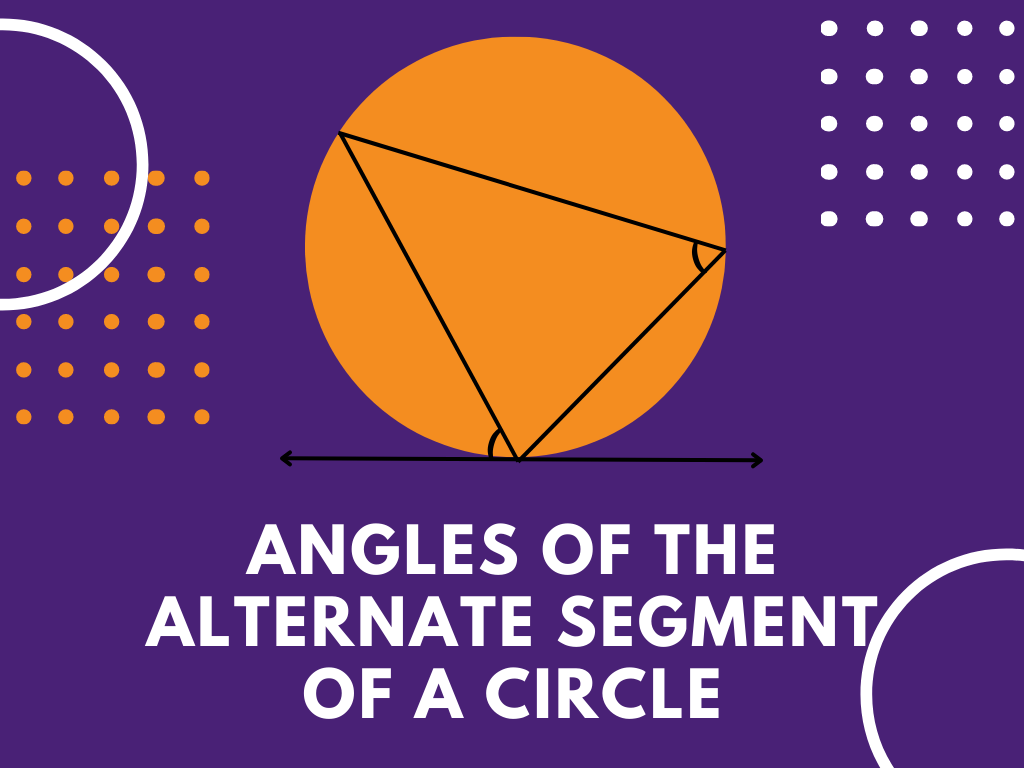
In a circle, if a tangent is drawn then at the point of contact we draw a chord. This chord divides the circle into two segments then the angle made by the chord with the tangent will be equal to the angle made in the alternate segment by the chord. This is the concept of Angles of the Alternate Segment of a Circle.
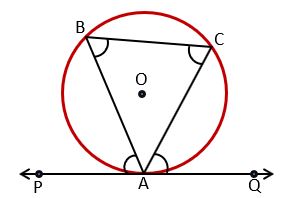
In the above figure, PQ is a tangent drawn at point A. AB and AC are chords drawn from the common point A. both chords divide the circle into two segments. Segments for chord AB are AB and ACB and segments for chord AC are AC and ABC.
∠PAB made by chord AB with tangent PQ in segment AB is equal to ∠ACB which is made in alternate segment ACB by chord AB.
Similarly, ∠QAC made by chord AC with tangent PQ in segment AC is equal to ∠ABC which is made in alternate segment ABC by chord AC.
Theorems Based on it
Theorem – 1) If a chord is drawn from a point of contact of the tangent of the circle then angles made by this chord with the tangent are equal to the respective alternate angles made by segments with this chord.
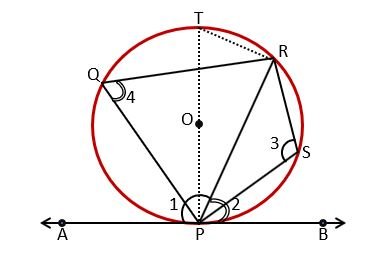
Given – AB is tangent at point P, chord PR makes angles ∠1 and ∠2 respectively with this tangent. Alternate angles of ∠1 and ∠2 are ∠3 and ∠4 respectively which are made in alternate segments at points S and Q.
Prove that – ∠1 = ∠3 and ∠2 = ∠4
Construction – Drawn diameter POT and joined TR.
Proof – In △PRT, ∠PRT = 90° [angle made by semicircle]
∴ ∠PTR + ∠RPT = 90° [the sum of the remaining two angles of a right-angled triangle] ———(1)
∵ ∠APT = 90° [radius is perpendicular to tangent]
∴ ∠RPT + ∠2 = 90° [radius is perpendicular to tangent] ————–(2)
From equations (1) and (2),
∠PTR + ∠RPT = ∠RPT + ∠2
∠PTR = ∠2 —————(3)
∵ ∠PTR = ∠4 [angles made in the same segment are equal] ————(4)
From equations (3) and (4),
∠2 = ∠4 —————(5)
∠1 + ∠2 = 180° [by linear pair angle] —————–(6)
∠3 + ∠4 = 180° [opposite angles in cyclic quadrilateral are supplementary] ———–(7)
From equations (6) and (7),
∠1 + ∠2 = ∠3 + ∠4
∵ ∠2 = ∠4 [from equation (5)]
Therefore, ∠1 = ∠3 Hence Proved.
Converse of Theorem
Theorem 2) If a line is drawn at one end of a chord of a circle in such a way that angles made with the chord are equal to alternate angles made by the chord in the segment then this line is the tangent line to the circle.
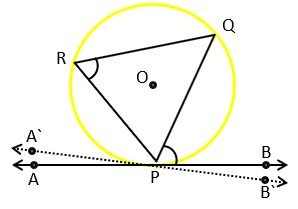
Given – PQ is the chord of the circle and at point P, line APB is drawn and ∠QPB = ∠PRQ.
Prove that – APB is a tangent.
Proof – Let A`PB` be the tangent line at the point P, instead of APB.
Then ∠QPB` = ∠PRQ ————(1)
∠QPB = ∠PRQ [given] ———(2)
From equations (1) and (2)
∠QPB` = ∠QPB ————(3)
From the figure, ∠QPB` = ∠QPB + ∠BPB` ————(4)
From equations (3) and (4)
∠QPB = ∠QPB + ∠BPB`
From the above equation, we can say that ∠BPB` is almost equal to zero
So, ∠BPB` = 0
This shows that lines APB and A`PB` coincide with each other.
It means line APB is tangent to the circle at point P. Hence Proved.
Some Examples –
Example 1) In the figure, PQ and RS are two tangents at points A and C respectively if ∠ABC = 70° and ∠BAQ = 50° then find ∠BCR.
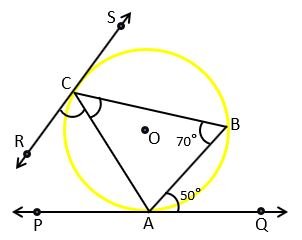
Solution – Tangent PQ is drawn at point A of chord AB So, by alternate segment angle theorem
∠BAQ = ∠ACB = 50°
Similarly, tangent RS is drawn at point C of chord AC.
So, ∠ABC = ∠ACR = 70°
Since ∠BCR = ∠ACB + ∠ACR
∠BCR = 50° + 70°
∠BCR = 120° Ans.
Example 2) In the given figure, AB is a tangent of a circle whose Centre is O which touches the circle at point C. if ∠ECB = 30° then find ∠DOC and ∠CEO.
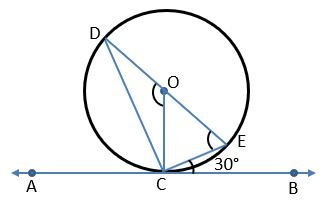
Solution – Given ∠ECB = 30°
∠ECB = ∠CDE = 30° [By alternate segment angle theorem for chord CE]
∠COE = 2∠CDE [Angle made on Centre is double the angle made on circle]
∴ ∠COE = 2⨯30° = 60° —————(1)
Now ∠DOC = 180° – ∠COE [By linear pair angle]
∠DOC = 180° – 60° [By equation (1)]
∠DOC = 120°
∠OCB = 90° [radius is perpendicular on a tangent]
∵ ∠ECB = 30°
∴ ∠OCE = ∠OCB – ∠ECB
∠OCE = 90° – 30°
∠OCE = 60° ————–(2)
In △OCE, ∠OCE + ∠CEO + ∠COE = 180°
60° + ∠CEO + 60° = 180°
∠CEO = 180° – 120°
∠CEO = 60° Ans.
Example 3) In the figure, ∠QPR = 70° and ∠PRQ = 30° then find ∠QRA and ∠PRB.
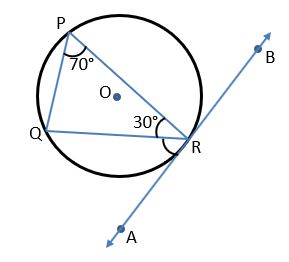
Solution – Given ∠QPR = 70° and ∠PRQ = 30°
∠QPR = ∠QRA = 70° [By alternate segment angle theorem for chord QR]
∴ ∠QRA = 70°
Now ∠PRB = 180° – (∠QRA + ∠PRQ) [Sum of angles on the straight line is 180°]
∠PRB = 180° – (70° + 30°)
∠PRB = 180° – (100°)
∠PRB = 80° Ans.
Angles of the Alternate Segment of a Circle Class 10th in Hindi
More About Angles of the Alternate Segment of a Circle