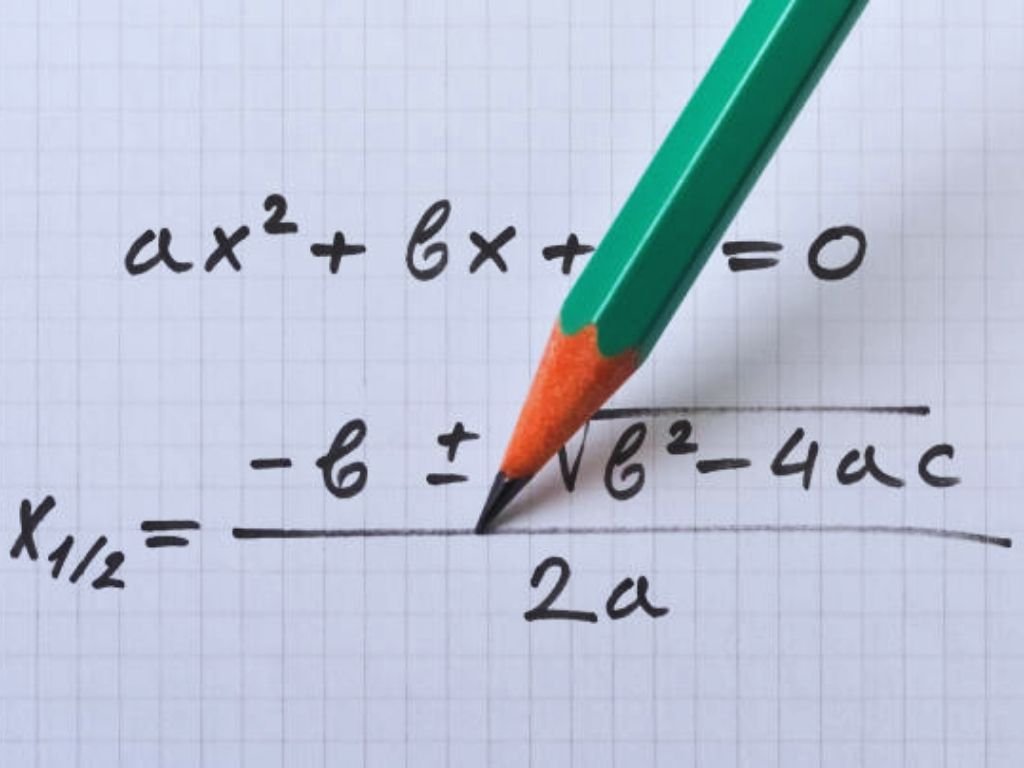Geometrical (Graphical) Meaning of the Zeroes of a Polynomial Class 10th

Introduction

We know that if a polynomial is p(x) and R is it’s zero then p(R) = 0. It means the zeroes of every polynomial satisfy it. Let’s understand this with the help of geometrical or graphical representation. In class 10th, We shall study the geometrical representation of linear polynomials, quadratic polynomials, and cubic polynomials, and also the geometrical meaning of the zeroes of a Polynomial.

1) For Linear Polynomial

As we know the general form of the linear polynomial is ax + b, where a ≠ 0. Let us take an example of the linear polynomial to understand the graphical representation.

Example – Represent the linear polynomial 3x + 6 graphically.

Solution – We know that the x-axis and y-axis are two axes in graph paper. So, we assume the given polynomial equals y.

Let y = 3x + 6

Now we shall find the different values of y for the different values of x.

x	-1	-3	0
y = 3x + 6	3	-3	6

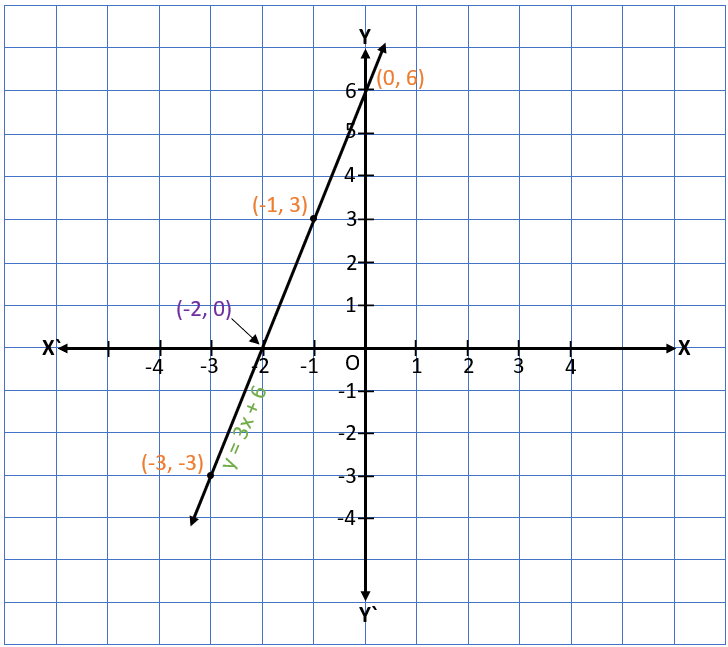
From the graph, we can see that graph of the linear polynomial is a straight line and if we extend the line it will intersect the x-axis at x = -2 so the point will be (-2, 0).

If we find the zero of the linear polynomial 3x + 6 directly.

3x + 6 = 0

3x = -6

x = -6/3

x = -2  

With the help of the graphical representation, we can understand that the zero of the linear polynomial 3x + 6 is the x-coordinate of the point at which the straight-line y = 3x + 6 intersects the x-axis.

For the general form of a linear polynomial,

General form ax + b where a ≠ 0

Zero of ax + b

ax + b = 0

ax = -b

x = -b/a

It means the zero of any linear polynomial ax + b is the x-coordinate of the point (-b/a, 0) where the graph straight-line y = ax + b intersects the x-axis.

Therefore, the linear polynomial has only one zero.

2) For Quadratic Polynomial

The general form of the quadratic polynomial is ax² + bx + c, where a ≠ 0. Let’s take an example to understand the graphical representation of quadratic polynomials.

Example – Represent the quadratic polynomial x² + 2x – 3 graphically.

Solution – We know that the x-axis and y-axis are two axes in graph paper. So, we assume the given polynomial equals y.

Let y = x² + 2x – 3

Now we shall find the different values of y for the different values of x.

x	-1	1	0	-3	-2
y = x2 + 2x – 3	-4	0	-3	0	-3

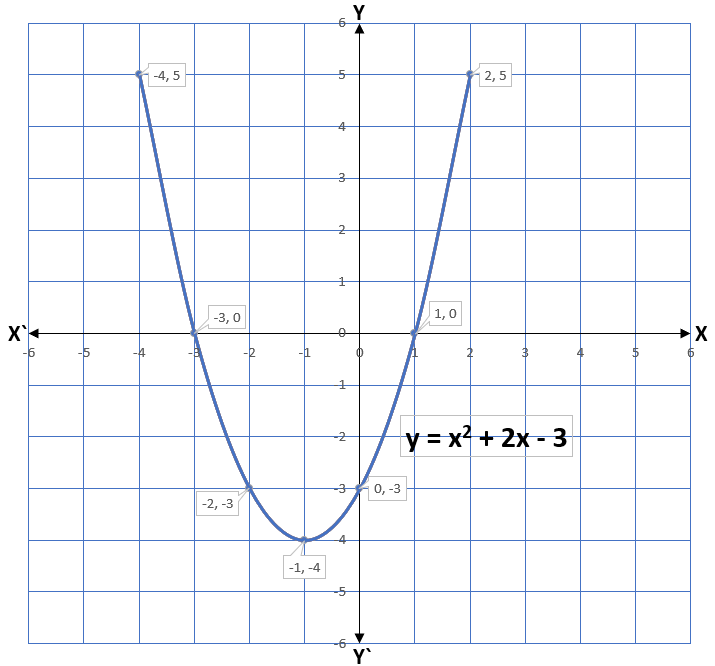
From the graph, we can see that graph of the quadratic polynomial is a parabola and the shape of the parabola is either open upwards or open downwards which depends on the value of a in the quadratic equation ax² + bx + c whether a > 0 or a < 0. The graph intersects the x-axis at two points (-3, 0) and (1, 0). Therefore, x = -3 and x = 1 are two zeroes.

If we find the zeroes of the quadratic polynomial x² + 2x – 3 directly.

x² + 2x – 3 = 0

x² + 3x – x – 3 = 0        [By Factorization method]

x(x + 3) – 1(x + 3) = 0

(x + 3)(x – 1) = 0

x + 3 = 0       and         x – 1 = 0

x = -3            and         x = 1 

With the help of the graphical representation, we can understand that the zeroes of the quadratic polynomial x² + 2x – 3 are the x-coordinate of the two points at which the parabola y = x² + 2x – 3 intersects the x-axis.

Therefore, the quadratic polynomial has two zeroes.

In the quadratic polynomial, there are three types of cases that can arise during the graphical representation.

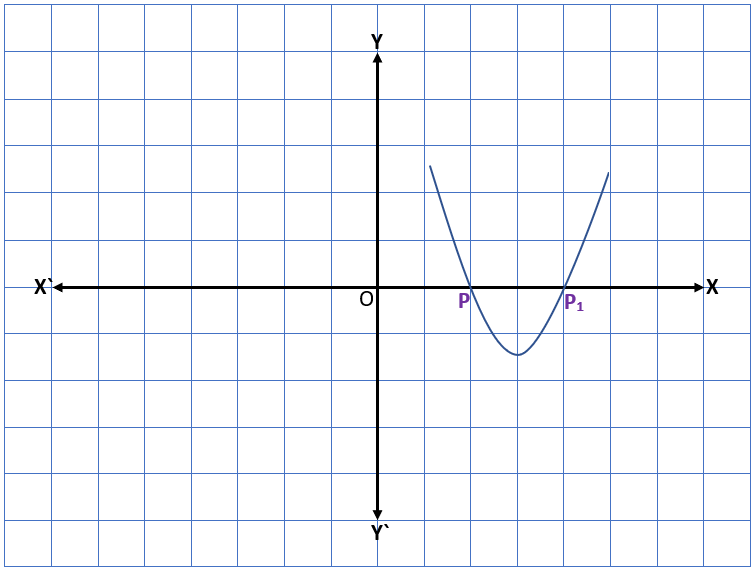
Case I – When the graph intersects the x-axis at two distinct (different) points P and P_1­. In this case, there are two zeroes of the quadratic polynomial ax² + bx + c and they are the x-coordinates of points P and P₁.

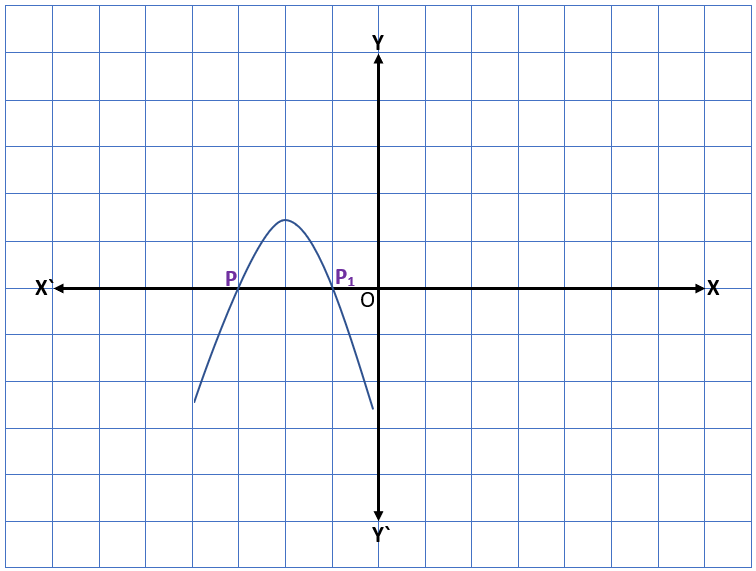
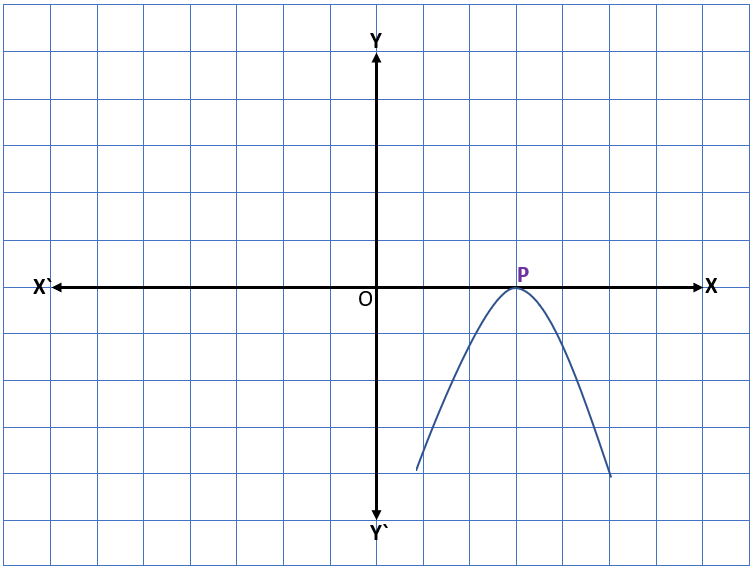
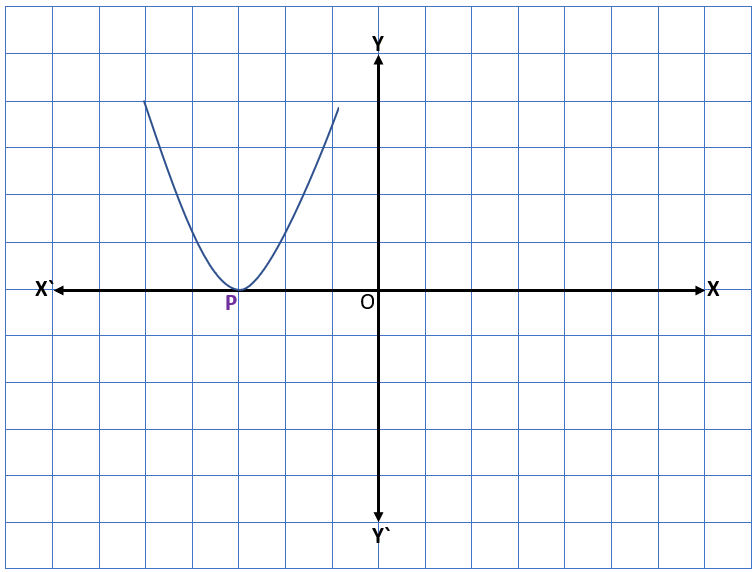
Case ll – In this case, the graph intersects the x-axis exactly at the same point. It means the two points coincide with each other so the points P and P₁ will become a single point P. Therefore, the x-coordinate of the point P will be only zero of the quadratic polynomial ax² + bx + c.

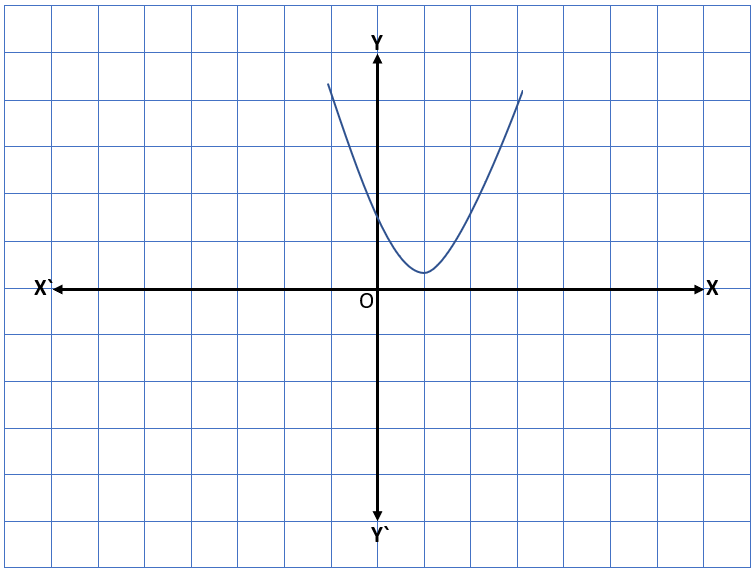
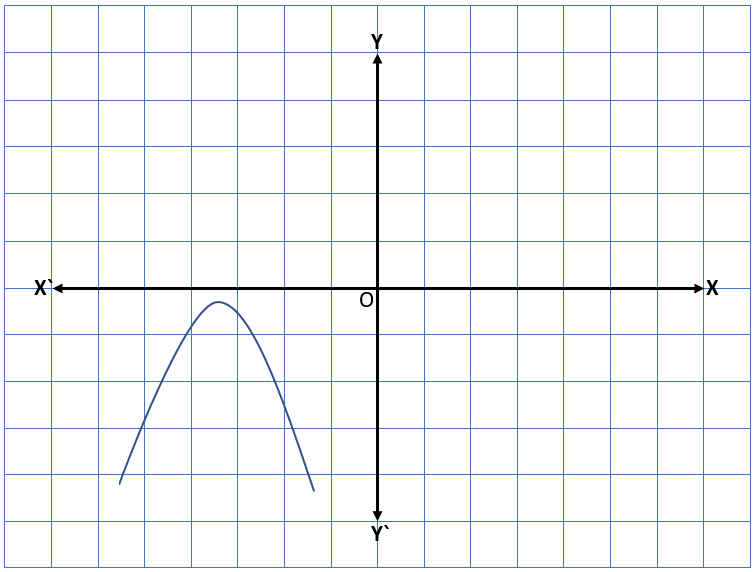
Case lll – In this case, the graph does not intersect the x-axis at any point but it is completely above the x-axis or below the x-axis. Therefore, in this case, there will be not any zero of the quadratic polynomial ax² + bx + c.

With the help of the above explanation, we can say that the quadratic polynomial can have either two zeroes or one zero (two equal zeroes) or no zero. We can also say that a polynomial having degree 2 has a maximum of two zeroes.

3) For Cubic Polynomial

As we have studied that the general form of the cubic polynomial is ax³ + bx² + cx + d, where a ≠ 0. What will be the graphical representation of the cubic polynomial let’s understand with the help of an example.

Example – Represent the cubic polynomial x³ – x graphically.

Solution – Let y = x³ – x

Now we shall find the different values of y for the different values of x.

x	-2	-1	0	1	2
y = x3 – x	-6	0	0	0	6

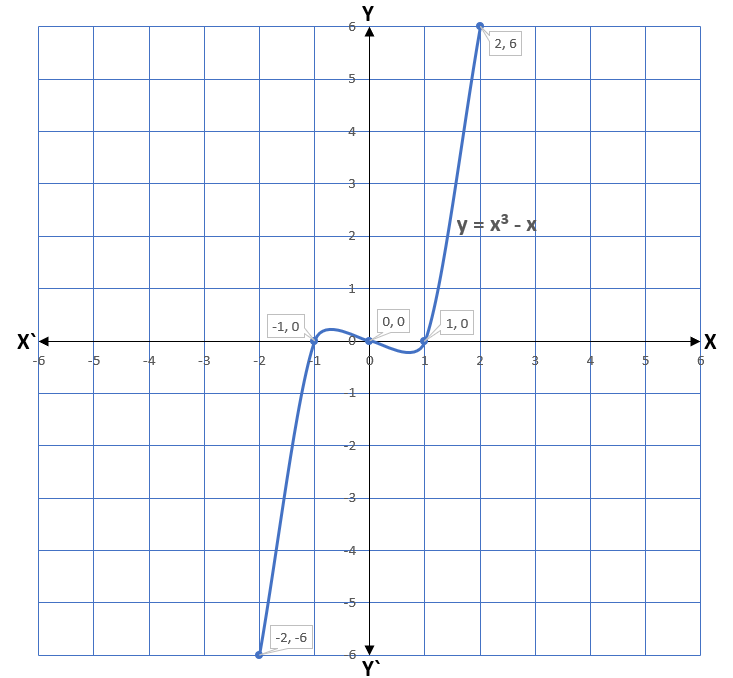
From the graph, we can see that graph of the cubic polynomial intersects the x-axis at three points (-1, 0), (0, 0), and (1, 0). Therefore, x = -1, x = 0 and x = 1 are three zeroes.

If we find the zeroes of the cubic polynomial x³ – x directly.

x³ – x = 0

x(x² – 1) = 0       

x = 0       and         x² – 1 = 0

x = 0       and         x² = 1

x = 0       and         x = ±√1 = ±1   

x = 0       and         x = +1 and -1

With the help of the graphical representation, we can understand that the zeroes of the cubic polynomial x³ – x are the x-coordinate of the three points at which the graph y = x³ – x intersects the x-axis.

Therefore, the cubic polynomial has three zeroes.

Let’s understand more about cubic polynomials with the help of some examples.

Example 1) Represent the cubic polynomial x³ graphically.

Solution – Let y = x³

x	-2	-1	0	1	2
y = x3	-8	-1	0	1	8

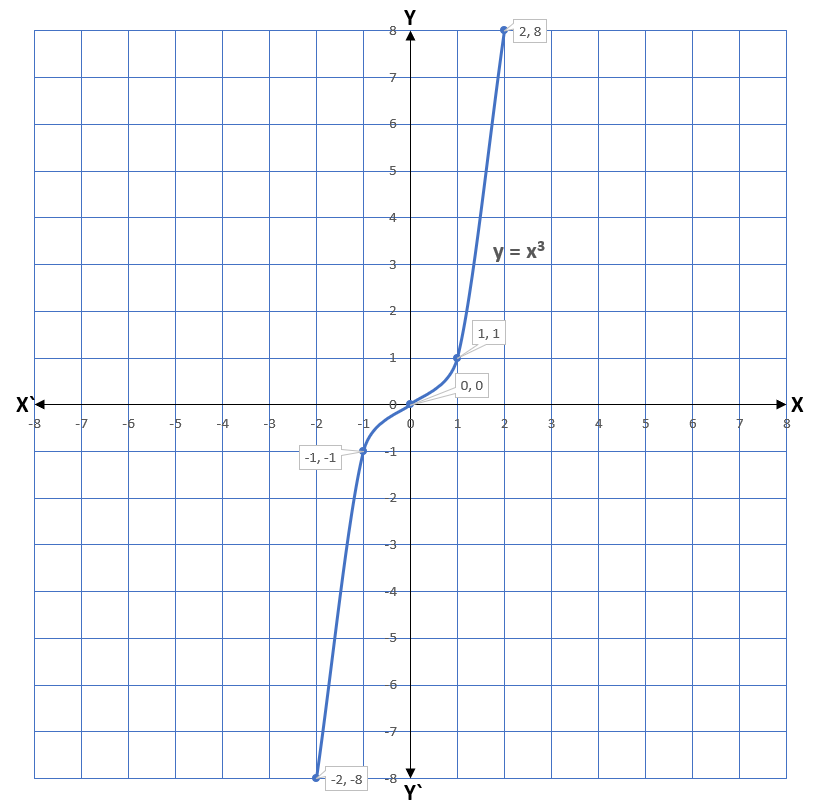
In this example, the graph intersects the x-axis at one point which is the origin. The coordinates of the origin are (0, 0) and the x-coordinate of the origin is always 0. Therefore, the zero of the cubic polynomial x³ is 0.

Example 2) Represent the cubic polynomial x³ – x² graphically.

Solution – Let y = x³ – x²

x	-2	-1	0	1	2
y = x3 – x2	-12	-2	0	0	4

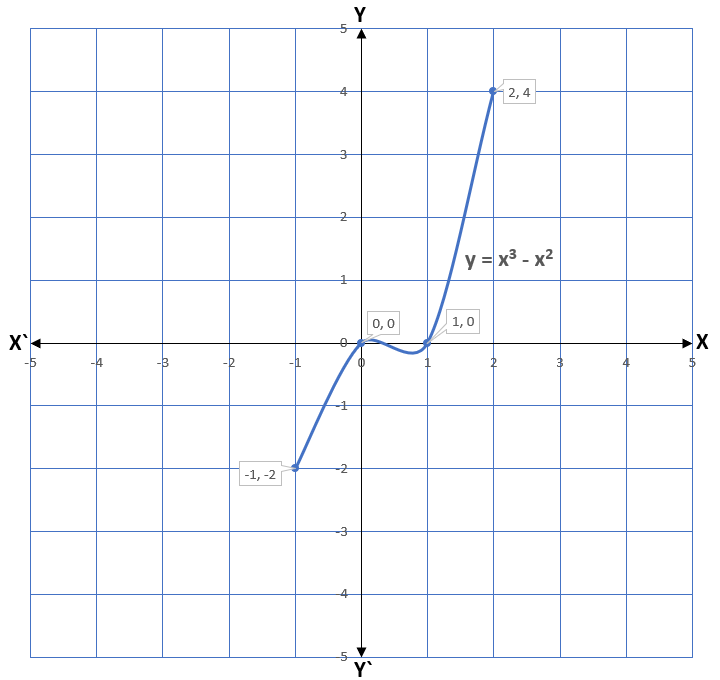
In the above example, the graph intersects the x-axis at two points which are the origin (0, 0) and (1, 0). The x-coordinates of both points are 0 and 1. Therefore, the zeroes of the polynomial x³ – x² are 0 and 1.

With the help of the above explanation, we can say that the cubic polynomial can have either three zeroes or two zeroes, or one zero. We can also say that a polynomial having degree 3 has a maximum of three zeroes.

Note – Generally, we can say that a polynomial of degree n has maximum n zeroes.

Geometrical (Graphical) Meaning of the Zeroes of a Polynomial in Hindi

More About Geometrical (Graphical) Meaning of the Zeroes of a Polynomial