Coordinate Geometry Class 9th

Introduction

In Class 9th, Before studying Coordinate Geometry (Analytical Geometry), We shall recall the number lines that how the number line is drawn, and how a number is represented on the number line. The number line shows positive and negative numbers in both directions. On the left side, negative numbers are written and on the right side, positive numbers are written. Both positive and negative numbers are infinite numbers. If we have to represent any number, we just point out that number on the number line. Although we point out the point on the number or in between two numbers. But there may be other situations that how can we get the exact position of the particular point. If the number is not on the number line, it is above or below the number line, then how do we represent that point? Let’s understand it with the help of an example.

Suppose we draw a rectangle and draw a dot in it as shown in the figure below.

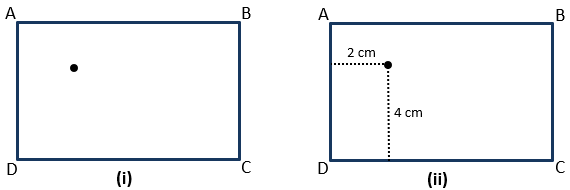
If we want to locate the exact position of the dot then how can we represent it? If we say that the dot is in the upper half of the rectangle or the dot is near the side AD of the rectangle or the dot is near vertex A. None of the statements help us to find the exact position of the point, but if we say that the dot is 2 cm away from the side AD then it helps something but not exactly. If we add some more to it and say that the dot is 4 cm above the side CD then we get the exact position of the dot. The above example shows that if there is a point in a plane and we want to know the position of that point then we need two fixed-line to locate it. In other words, we need two independent pieces of information to locate the point.

Cartesian System

Rene Descartes discovered the system used for describing the position of a point in a plane. In honor of Rene Descartes, this system is known as the Cartesian system. We know that in the number line, there are positive and negative numbers and 0 in the middle. The difference between the two numbers is equal to 1 unit on the number line. We take the distance in any direction (positive or negative) from point O. This point is called Origin.

Descartes discovered the system by placing the two number lines perpendicular to each other to locate a point. In these two perpendicular number lines, one line is horizontal and another is vertical. To understand it clearly, here is the figure.

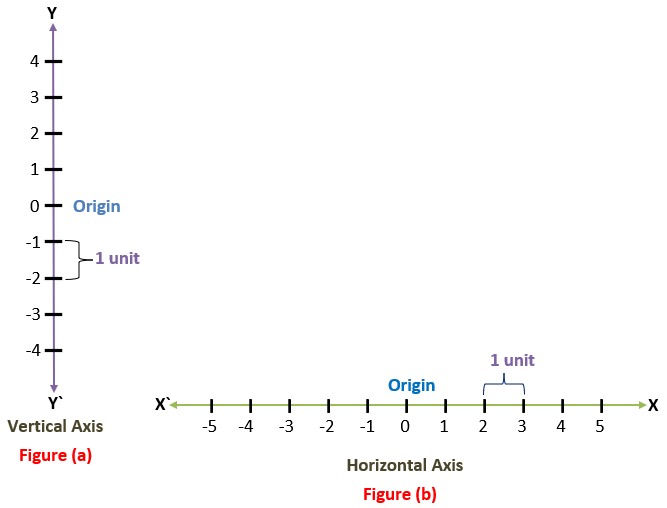
In figure (a), the vertical number line YY` is drawn which is called the vertical axis and in figure (b), the horizontal number line XX` is drawn which is called the horizontal axis. If we combine both the number lines perpendicularly at their origins then the horizontal number line XX` is called the x-axis and the vertical number line YY` is called the y-axis. The point where both the lines intersect each other is called the origin and is denoted by O.

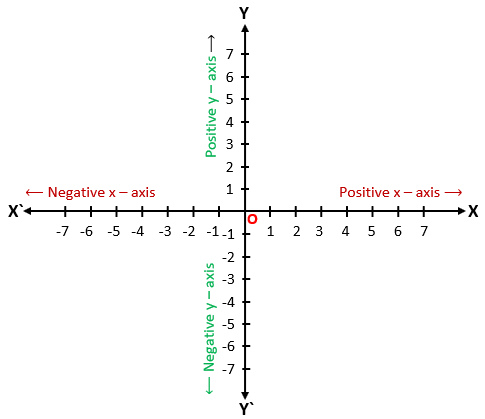
Here, there are four directions from the origin, two directions OX and OY are positive directions of the x-axis and y-axis respectively, and the other two directions OX` and OY` are negative directions of the x-axis and y-axis respectively.

In the above figure, we can see that both axes divide the plane into four equal parts. These four parts are called Quadrants. Quadrant means one-fourth part. The numbering of the quadrants starts from the OX (Positive x-axis) in the anticlockwise direction. Quadrants are numbered I, II, III, and IV. Here is the figure.

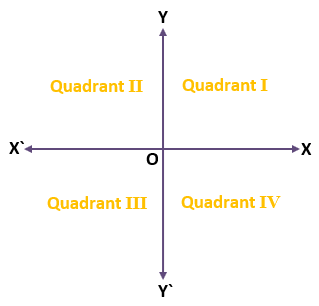
The plane in which the x-axis and y-axis are present with four quadrants is called the Cartesian plane or XY plane or Coordinate plane. The x-axis and y-axis are called Coordinate axes.

In these quadrants, how to find the position of a point, and in which quadrant the point is? How can we get the exact position of any point and what will be the location? These types of questions are raised in our minds. Let’s see how to solve these.

Let us assume a point P which is situated in quadrant I and we have to find the location of point P.

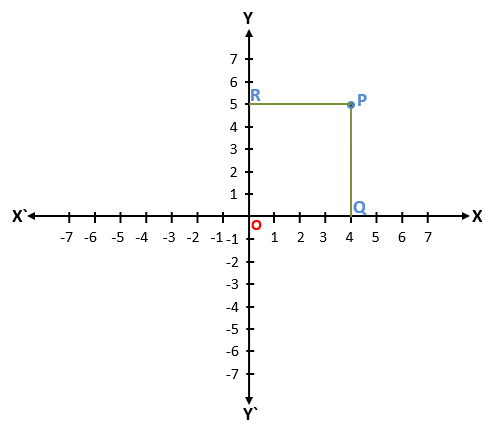
First of all, we draw perpendicular on the x-axis and y-axis from point P as shown in the above figure. The perpendicular drawn on the x-axis is PQ and on the y-axis is PR.

Here, PQ ∥ OR and PR ∥ OQ

So, PQ = OR = 5 units and PR = OQ = 4 units

The perpendicular distance from the y-axis is PR which is equal to OQ, which gives the value on the positive x-axis (x = +4). The value of x is the x – coordinate (in both directions)

The perpendicular distance from the x-axis is PQ which is equal to OR, which gives the value on the positive y-axis (y = +5). The value of y is the y – coordinate (in both directions)

Abscissa – The perpendicular distance of a point from the y-axis which gives the value of the x – coordinate is called Abscissa. For point P, Abscissa is +4 (x = +4).

Ordinate – The perpendicular distance of a point from the x-axis which gives the value of the y – coordinate is called Ordinate. For point P, the Ordinate is +5 (y = +5).

We can see that there are two values of point P in two directions (positive x-axis and positive y-axis). These two values are called the Coordinates of a point. In these two values, one value is of x (whether positive or negative depends on the direction) and another value is of y (whether positive or negative depends on the direction).

Here, for point P, x = 4 and y = 5

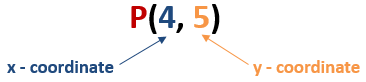
To write in the form of coordinates first we write the value of the x-coordinate and then we write the value of the y-coordinate in the bracket which is separated by a comma.

So, the coordinate of point P (4, 5)

Note – 1) Every point has its unique coordinates so it is not possible to have the same coordinates of two different points. We have to understand that coordinates (1, 2) and (2, 1) are not equal and (-3, -4) ≠ (3, 4).

2) If the point is situated on the x-axis, then the y – coordinate will be zero. The coordinates of a point situated on the x-axis are of the form (x, 0). And if the point is situated on the y-axis, then the x – coordinate will be zero. The coordinates of a point situated on the y-axis are of the form (0, y).

3) Coordinates of the origin are (0, 0) because the perpendicular distance of the origin from both axes is always zero.

Signs of Coordinates in Quadrants

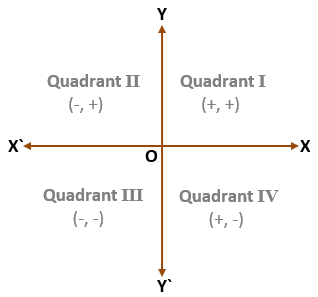
1. In Quadrant I, values of the x and y coordinates of a point are positive because it is bounded by the positive x-axis (OX) and positive y-axis (OY). If a point has both the coordinates positive then that point will be situated in the First Quadrant.
2. In Quadrant II, the value of the x – coordinate of a point is negative and the value of y – coordinate is positive because it is bounded by the negative x-axis (OX`) and positive y-axis (OY). If the x-coordinate of a point is negative and the y-coordinate is positive, then that point will be situated in the Second Quadrant.
3. In Quadrant III, values of the x and y coordinates of a point are negative because it is bounded by the negative x-axis (OX`) and negative y-axis (OY`). If a point has both the coordinates negative then that point will be situated in the Third Quadrant.
4. In Quadrant IV, the value of the x – coordinate of a point is positive and the value of the y – coordinate is negative because it is bounded by the positive x-axis (OX) and negative y-axis (OY`). If the x-coordinate of a point is positive and the y-coordinate is negative, then that point will be situated in the Fourth Quadrant.

Example 1) With the help of the figure, give the answers to the questions.

1. What is the coordinate of point c? In which Quadrant is it situated?
2. If the coordinate of point B is (-3, 3) then write abscissa and ordinate.
3. Write the coordinates of points A and D.

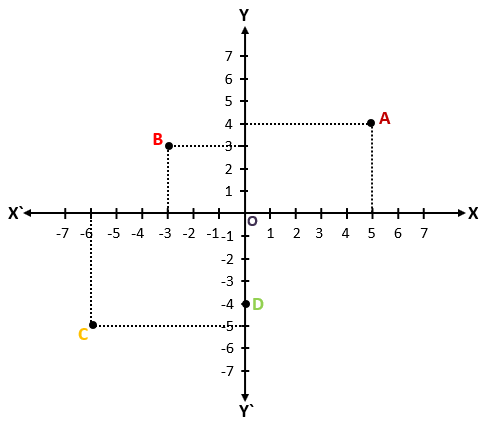
Solution – 1) Coordinate of point C is (-6, -5) and it is situated in the Third Quadrant.

2) Coordinate of point B is (-3, 3) then abscissa = -3 and ordinate = 3                 

3) Coordinate of point A is (5, 4) and the Coordinate of point D is (0, -4).              Ans.

Example 2) If a point is situated on the x-axis, 7 units away from the y-axis in a positive direction then write the coordinate of this point.

Solution – Coordinates of this point will be (7, 0) because this point is situated on the x-axis means its y – coordinate will be zero and it is 7 units away from the y-axis in a positive direction which means it is situated on the positive x-axis.

Plotting of a Point if its Coordinates are given

If the coordinates of a point are given, we can plot it in a plane. This process is called ‘plotting of a point’. Let us understand it with an example.

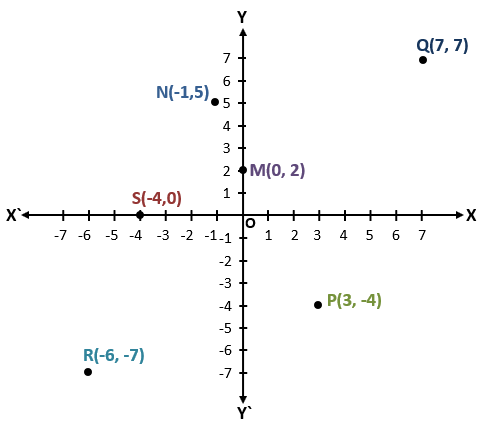
Example – Plot the points M(0, 2), N(-1, 5), P(3, -4), Q(7, 7), R(-6, -7), S(-4, 0) in the Cartesian plane.

Solution – First of all, we draw a Cartesian plane. Taking 1 cm = 1 unit. Then we shall plot all the points. Before we start plotting, one thing we have to keep in mind is that in the given coordinates the first value is of x – coordinate, and the second value is of y – coordinate. We cannot interchange these values otherwise our plotting will be wrong.

Some Questions

Q 1) What is the other name of x – coordinate?

Ans. – Abscissa

Q 2) What is the other name of y – coordinate?

Ans. – Ordinate

Q 3) What is Cartesian plane?

Ans. – The plane in which the x-axis and y-axis are present with four quadrants is called the Cartesian plane.

Q 4) What is the coordinate axis?

Ans. – Both the x-axis and y-axis are called coordinate axes.

Q 5) What is Quadrant?

Ans. – The coordinate axes divide the plane into four parts, each part is called Quadrant.

Q 6) What is Origin?

Ans. – The intersection point of the x-axis and y-axis is called Origin.

Q 7) What are x – coordinate (Abscissa) and y – coordinate (ordinate)?

Ans. – x – coordinate (Abscissa) – The perpendicular distance of a point from the y-axis is called x – coordinate (Abscissa).

y – coordinate (ordinate) – The perpendicular distance of a point from the x-axis is called y – coordinate (ordinate).

Q 8) What are the coordinates of Origin?

Ans. – O (0, 0)

Coordinate Geometry (Analytical Geometry) Class 9^th in Hindi

More About Coordinate Geometry (Analytical Geometry)