Perimeter and Area Class 6th

Introduction

In this section, we shall study the Perimeter and Area for class 6^th of plane figures. The Perimeter of the plane figures is the measure related to its Boundary and the Area of the plane figures is the measure related to its region or surface occupied by it.

What are Plane Figures?

Plane figures are two-dimensional figures which are drawn on the plane surface.

Open Figures

In the open figures, the starting point and the ending point of the figure are not at the same point. The figures in which the starting point and the ending point are not joined, are called open figures.

Starting point – A, Ending point – B

Closed Figures

In the closed figures, the starting point and the ending point of the figure are at the same point. The figures in which the starting point and the ending point are joined, are called closed figures.

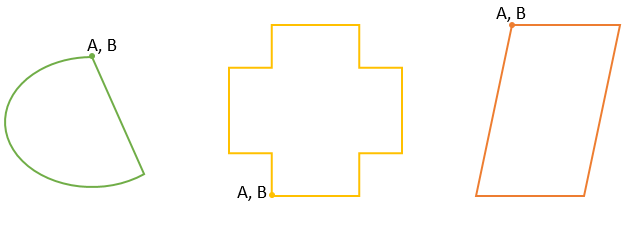
Starting point – A, Ending point – B

What is Perimeter?

Perimeter is the complete measurement of the boundary of the closed figures. The Perimeter of the closed figures can be found but not of the open figures.

In the above figures, to calculate the perimeter we start from point A and the complete measurement is from point A to point A.

For figure (1), Perimeter = AB + BC + CA

For figure (2), Perimeter = AB + BC + CD + DA

For figure (3), Perimeter = AB + BC + CD + DA

The Perimeter of Irregular Shapes

Irregular shapes are figures that have all the sides and all the angles of different measures. Such types of figures are called irregular closed figures. The Perimeter of irregular shapes is the total of all sides. Let’s understand with examples.

Example – find the perimeter of the figures given below.

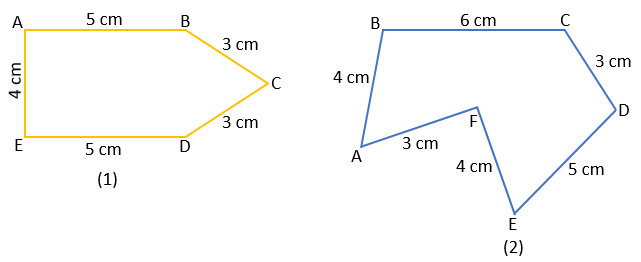
Solution –

Perimeter of figure (1) = AB + BC + CD + DE + EA

= 5 cm + 3 cm + 3 cm + 5 cm + 4 cm

= 20 cm          Ans.

Perimeter of figure (2) = AB + BC + CD + DE + EF + FA

= 4 cm + 6 cm + 3 cm + 5 cm + 4 cm + 3 cm

= 25 cm           Ans.

The Perimeter of Regular Shapes

The figures that have all the sides and all the angles of the same measure are called Regular shapes. These types of figures are called Regular closed figures. For regular shapes, we can find the perimeter by multiplying the number of sides by the measure of each side. We can understand it by the example solved below.

Example – Find the perimeter of the figures given below.

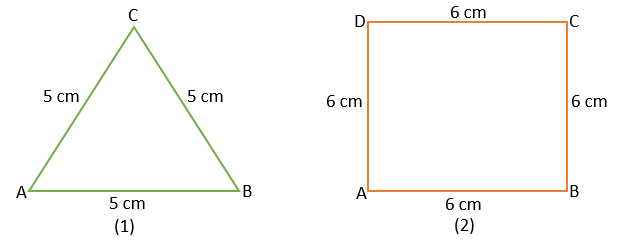
Solution –

In figure (1), all three sides of the triangle are equal which means this triangle is an equilateral triangle.

Therefore, The Perimeter of an Equilateral Triangle = 3×Side

= 3×5 cm = 15 cm           Ans.

In figure (2), all four sides are equal so it is a square.

Therefore, The Perimeter of the Square = 4×Side

= 4×6 cm = 24 cm           Ans.

Note – We can make a general formula to find the perimeter of a regular shape.

The perimeter of a Regular shape = Number of sides × Measure of each side

The Perimeter of a Rectangle

We know that in a rectangle, there are four sides and the opposite sides are equal. So how can we find the perimeter of a rectangle? Let’s see.

The above figure is a rectangle ABCD. Opposite sides will be equal so AB = CD and BC = AD.

Now, perimeter of rectangle ABCD = AB + BC + CD + DA

= AB + BC + AB + BC [∵ AB = CD and BC = AD]

= 2AB + 2BC

= 2(AB + BC)

Here, AB = Length of the rectangle and BC = Breadth of the rectangle.

So, we can write as the formula, Perimeter of Rectangle = 2(Length + Breadth)

It means if we have to find the perimeter of a rectangle, we have to add length and breadth and then multiply by 2.

Example – Find the perimeter of the rectangle given below.

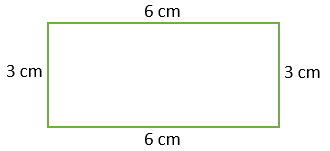
Solution – Perimeter of the rectangle = 2(Length + Breadth)

= 2(6 cm + 3 cm)

= 2(9 cm)

= 18 cm           Ans.

Note – 1) Perimeter is a type of Distance so the unit of the perimeter is a length unit.

2) Larger figures have a larger perimeter.

What is Area?

When we draw a closed figure, the figure covers the region which is enclosed by that. That region is known as the Area of the figure. Here are some closed figures.

All the above figures cover some amount of surface. We can see that the figure which is larger is covering more amount of the surface. Sometimes we can’t say which figure has more area. In this condition, we use squared paper or graph paper to calculate the area. Let’s take an example.

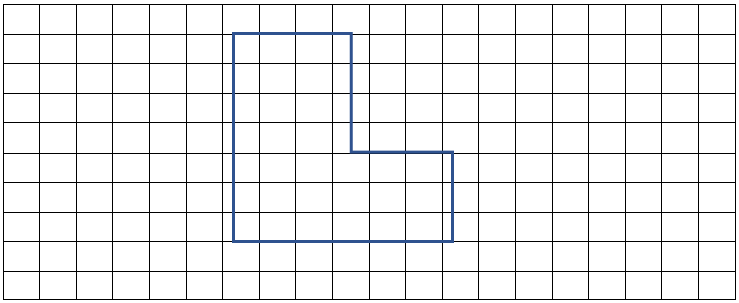
In the squared paper, each side of every square is of the measure 1 cm. to calculate the area on squared paper, we have to keep notice of some rules.

1. The square which is completely covered under the figure is counted as a full square.
2. The square which is half covered under the figure is counted as half square.
3. The square which is covered less than half is not counted.
4. The square which is covered more than half is counted as a full square.

Now, in the above example,

Number of squares that are completely covered = 23 squares

Number of squares that are half covered = 4 = 2 full squares

Number of squares which are covered less than half = 3 squares (not counting)

Number of squares which are covered more than half = 7 squares (counting as full squares)

Therefore, the area of the given figure will be = 23 + 2 + 7

= 32 square unit

Note – We measure the area of any closed figure in a square unit. If the sides of a figure are in centimeters then the unit of the area will be square centimeters (sq. cm.).

Area of Rectangle

If we draw a Rectangle on squared paper and calculate the area, then we shall find that the squares covered by the rectangle are equal to the multiplication of its length and breadth.

Squares covered by the Rectangle = 24 squares

Multiplication of length and breadth = 6×4 = 24

Since squares covered by the rectangle and the multiplication of length and breadth are equal. 

So, we can calculate the area of a rectangle by multiplying the length and breadth of the rectangle.

Therefore, Area of Rectangle = Length × Breadth

Example – If the length and breadth of a rectangular table are 10 cm and 7 cm respectively, then find the area of the table.

Solution – Here, the length of the table = 10 cm

Breadth of table = 7 cm

So, the area of the rectangular table = length × breadth

= 10 cm × 7 cm

= 70 square cm.             Ans.

Area of a Square

The Area of the square can be found the same as the area of the rectangle. We know that if the length and breadth of a rectangle are the same then that will be a square.

Squares covered by the square = 16 squares

Multiplication of its two sides = 4×4 =16

Since both values are the same so we can calculate the area of a square by multiplying its two sides.

Therefore, Area of Square = Side × Side

Example – Find the area of a square-shaped tile, if each side is 5 cm.

Solution – Each side of a square-shaped tile = 5 cm

So, the area of a square-shaped tile = side × side

= 5 cm × 5 cm

= 25 sq. cm.        Ans.

Perimeter and Area Class 6^th in Hindi

More About Perimeter and Area