The Similarity of Triangles Class 10th

Introduction

The triangle is the shape, we are well known about it and its properties. We have studied different triangles and terms related to them like a scalene triangle, equilateral triangle, isosceles triangle, the area of the triangle, the perimeter of a triangle, the median of a triangle, the altitude of the triangle, etc. In the previous class, we also studied the congruence of triangles and different criteria for the congruency of triangles. According to congruency, two triangles are congruent if their shape and size are the same. Congruent triangles are mirror images of each other. In this class, we shall study the similarity of triangles, criteria for similarity, properties, and areas of similar triangles with the help of different types of examples.

Similar Figures

Similar figures are figures which have the same shape but not the same size. Two figures that have the same shape are called Similar Figures. In similar figures, it is not necessary to have the same size. Let’s understand with the help of some figures.

In Figure (i), the shape diamonds are drawn of different sizes. Are all the diamonds congruent? All the diamonds are not congruent but some of those (figures 2 and 3) are congruent because of the same size. All the diamonds are of the same shape so all are similar figures.

Similarly, in Figure (ii) and Figure (iii), all the circles and all the triangles are similar figures because of the same shape. In both Figure (ii) and Figure (iii), some of the circles (figures 2 and 4) and some of the triangles (figures 1 and 3) are congruent because of the same size.

From the above figures, we can say that all the congruent figures are similar but all the similar figures are not necessarily congruent.

Note – One thing should be also noticed that only the same types of figures can be similar, not different types of figures. It means a circle can be similar to another circle and a triangle can be similar to another triangle. A circle can’t be similar to a triangle because both are different types of figures.

What happens when two figures look similar but we cannot sure about them? Therefore, we need some conditions or a definition to make rules to ensure whether the given two figures are similar or not. Let us understand with the help of an example.

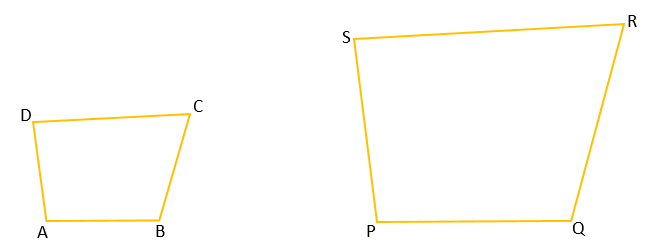
As we can see that quadrilaterals ABCD and PQRS look similar but there is some uncertainty between them. In this condition, if we have the measurement of each side of quadrilateral ABCD and we increase each side by a fixed measure. Then the ratio or proportion of each side of quadrilateral ABCD with each corresponding side of quadrilateral PQRS will be equal. Let’s understand this clearly with the help of the above figures.

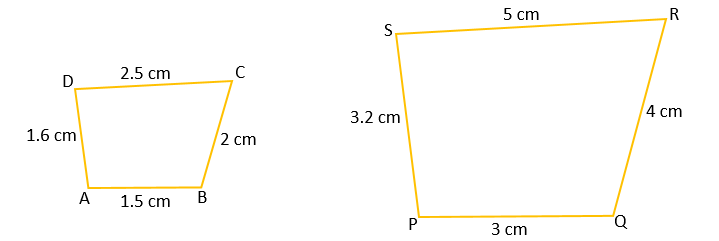
According to the figures, in quadrilaterals ABCD and PQRS, we write measurements of corresponding sides.

AB = 1.5 cm and PQ = 3 cm

BC = 2 cm and QR = 4 cm

CD = 2.5 cm and RS = 5 cm

DA = 1.6 cm and SP = 3.2 cm

Now, taking the ratio of corresponding sides,

AB/PQ = 1.5/3 = ½

BC/QR = 2/4 = ½

CD/RS = 2.5/5 = ½

DA/SP = 1.6/3.2 = ½

Or we can write, AB/PQ = BC/QR = CD/RS = DA/SP = ½

With the help of this example, we can understand that in both quadrilaterals ABCD and PQRS, the ratio of corresponding sides is equal. It means each side of quadrilateral ABCD is increased by equal measure. Therefore, both quadrilaterals are similar on the basis of their sides. But what about their angles? Are the angles of both quadrilaterals ABCD and PQRS equal? Angles of both quadrilaterals should be equal otherwise they will be not the same shape and will not be similar.

According to the angle property, the angle between two-line segments depends on their inclination, not on their measurements. The same property is applicable here for the above quadrilaterals ABCD and PQRS. So, all the corresponding angles of both quadrilaterals will be equal.

In quadrilaterals ABCD and PQRS, equal corresponding angles are as follows.

∠A = ∠P = 95°

∠B = ∠Q = 110°

∠C = ∠R = 85°

∠D = ∠S = 70°

Definition of Similarity

The above-detailed explanation helps us to state the definition of similarity. Triangles, quadrilaterals, etc., are the types of polygons so the definition is for two polygons. Two polygons of the same number of sides are said to be similar if their corresponding sides are in the same ratio and their corresponding angles are equal.

Condition for Similarity

According to the definition, there are two conditions for the similarity of the polygon of the same number of sides. The two conditions are as follows –

1) Corresponding angles of both the polygon must be equal.

2) Corresponding sides of both polygon must be in the same ratio.

Both conditions are important and compulsory for the similarity of polygons. Either of the two conditions 1) and 2) of similarity of two polygons is not sufficient for them to be similar.

If there are two polygons and their corresponding sides are in the same ratio but the corresponding angles are not equal then they are not similar. Similarly, if their corresponding angles are equal but corresponding sides are not in the same ratio then they are also not similar.

Note – If there are two similar polygons and a third polygon is also similar to one of them then all three polygons are similar to each other.

Criteria for Similarity of Triangles

Properties of Similar Triangles

Areas of Similar Triangles

Some Examples

The Similarity of Triangles Class 10th in Hindi

More About The Similarity of Triangles