Angle Subtended by a Chord of Circle Class 10th

Introduction

In a circle, if we draw a chord and join the two ends of the chord to the third point which is situated at the Centre or on the circle, then the angle made at the third point is the angle subtended by the chord of the Circle.

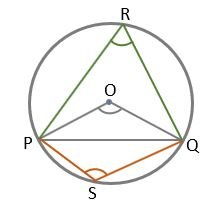
In the above figure, ∠PRQ and ∠PSQ are the angles subtended by the chord PQ on the points R and S in major and minor segments respectively. ∠POQ is the angle subtended by the chord PQ at the Centre of the circle.

In a circle, if we draw two chords of equal lengths then the angles subtended by both the chords at the Centre of the circle are equal. We can prove this statement by theorem.

Explanation and Theorems Based on it

Theorem 1) Equal chords of a circle subtend equal angles at the Centre.

Given – Chords PQ = RS

Prove that – ∠POQ = ∠ROS

Proof – In △POQ and △ROS

PQ = RS (equal chords given)

OP = OR (Radii of the same circle)

OQ = OS (Radii of the same circle)

By the SSS rule, △POQ ≅ △ROS

So, corresponding parts of congruent triangles (CPCT) will be equal.

Therefore,      ∠POQ = ∠ROS         Hence Proved.

The converse of the above theorem is also true and here is its proof.

Converse of Theorem

Theorem 2) If the angles subtended by the chords of a circle at the Centre are equal, then the chords are equal.

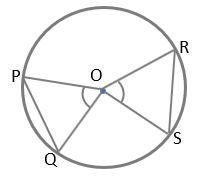
Given – ∠POQ = ∠ROS

Prove that – PQ = RS

Proof – In △POQ and △ROS

OP = OR (Radii of the same circle)

∠POQ = ∠ROS (equal angles given)

OQ = OS (Radii of the same circle)

By SAS rule, △POQ ≅ △ROS

So, by CPCT         PQ = RS                   Hence Proved.

Perpendicular to a Chord from the Centre

In a circle, if we draw a perpendicular to a chord from the Centre then the perpendicular divides the chord into two equal parts. That means it bisects the chord. It can be proved by the theorem.

Theorem 3) The perpendicular drawn from the Centre of a circle to the chord bisects the chord.

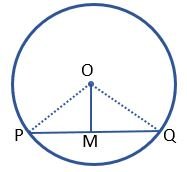
Given – PQ is a chord and OM ⊥ PQ

Prove that – PM = MQ

Construction – Joined Centre O to P and Q.

Proof – In △POM and △QOM,

OP = OQ (radii of the same circle)

∠OMP = ∠OMQ = 90° (given OM ⊥ PQ)

OM = OM (common side)

By RHS rule, △POM ≅ △QOM

So, by CPCT,       PM = MQ Hence Proved.

The Converse of the Above Theorem

Theorem 4) The line joining the Centre of the circle to the midpoint of the chord is perpendicular to the chord.

Given – M is the midpoint of chord PQ, it means PM = MQ

Prove that – OM ⊥ PQ

Construction – Joined Centre O to P and Q.

Proof – In △POM and △QOM,

OP = OQ (radii of the same circle)

PM = MQ (given)

OM = OM (common side)

By the SSS rule, △POM ≅ △QOM

So, by CPCT, ∠OMP = ∠OMQ ————–(1)

∠OMP + ∠OMQ = 180° (by linear pair of angles)

∠OMP + ∠OMP = 180° [from equation (1)]

2∠OMP = 180°

∠OMP = 180°/2 = 90°

Therefore, ∠OMP = ∠OMQ = 90°

So,          OM ⊥ PQ           Hence Proved.

Chords in a Circle and their Distances from the Centre

In a circle, if we draw chords of different lengths then we observe that the chord which is shorter in length is far from the Centre and the chord which is longer in length is near to the Centre.

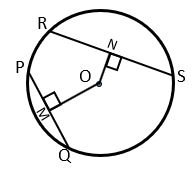
In the figure, there are two chords PQ and RS drawn. Where chord RS > chord PQ. The distance from the Centre (perpendiculars drawn from the Centre) of both the chords are OM and ON respectively. We can clearly see that distance OM > ON. It shows that chord PQ is Smaller than RS so RS is nearer to the Centre than PQ.

If Chords are Equal – If we draw two equal chords then the distance of both the chords from the Centre will be equal. This can be understood by the figure drawn below.

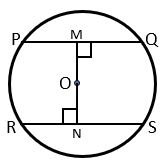
In the figure, there are two equal chords PQ and RS and their distance from the Centre is OM and ON respectively. If we measure both distances, we will find that both distances are equal. It means that equal chords have an equal distance from the Centre.

Theorem 5) Equal chords of a circle are equidistant from the Centre.

Given – Chords AB = CD

Prove that – OP = OQ

Construction – Joined points A and D to Centre O.

Proof – ∵ OP ⊥ AB

∴ AP = PB = ½ AB (Perpendicular drawn from the Centre to a chord bisects the chord)

And OQ ⊥ CD

∴ CQ = QD = ½ CD (Perpendicular drawn from the Centre to a chord bisects the chord)

Here, AB = CD (given)

∴ AP = QD    ————(1)

Now, In △APO and △DQO,

AP = QD [from equation (1)]

OA = OD [Radii of the same circle]

∠APO = ∠DQO = 90°

By RHS rule, △APO ≅ △DQO

So, by CPCT,          OP = OQ                   Hence Proved.

Note – In the congruent circles, equal chords are equidistant from their corresponding Centres.

Converse of Theorem

Theorem 6) Chords equidistant from the Centre of a circle are equal in length.

Given – OP = OQ

Prove that – AB = CD

Construction – Joined points A and D to Centre O.

Proof – In △APO and △DQO,

OP = OQ (given)

OA = OD (Radii of the same circle)

∠APO = ∠DQO = 90°

By RHS rule, △APO ≅ △DQO

So, by CPCT,      AP = QD

Multiplying both sides by 2

2AP = 2QD   [∵ AP = PB and CQ =QD]

Therefore, AB = CD          Hence Proved.   

Note – Chords of congruent circles which are equidistant from the corresponding Centres are equal in length.

Example

Example – In the given figure, the radius of a circle with Centre O is 6 cm. If OA ⊥ PQ, OB ⊥ RS, PQ ∥ RS, PQ = 10 cm and RS = 8 cm. Then find AB.

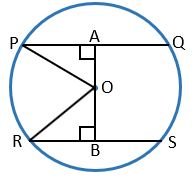
Solution – ∵ OA ⊥ PQ and OB ⊥ RS

∴ PA = AQ = ½ PQ [perpendicular drawn from the Centre to a chord bisects the chord]

= ½⨯10 = 5 cm

RB = BS =  RS [perpendicular drawn from the Centre to Chord bisects the chord]

= ½⨯8 = 4 cm

Radius OP = OR = 6 cm

In △PAO, by Pythagoras theorem,

OA² = OP² – PA²

OA² = (6)² – (5)²

OA² = 36 – 25 = 11

OA = √11 = 3.32 cm (Approximately)

Now, in △RBO, by Pythagoras theorem,

OB² = OR² – RB²

OB² = (6)² – (4)²

OB² = 36 – 16 = 20

OB = √20 = √(4⨯5)  

OB = 2√5  = 2⨯2.2360 = 4.47 cm (Approximately)

Therefore, AB = OA + OB

AB = 3.32 + 4.47

AB = 7.79 cm          Ans.

Angle Subtended by a Chord of Circle Class 10^th in Hindi

More About Angle Subtended by a Chord of Circle