Lines and Angles Class 9th

Introduction

In the previous classes, we studied line segments, rays, and lines and their properties. We also know the difference between them. Now, we shall study lines and angles, the formation of angles with the help of lines, theorems based on the properties, etc.

We also know the importance of lines and angles in our daily life. In our houses, examples of lines are iron or steel rods in the windows or doors, different types of linear designs and examples of angles are angles made between walls and floor, the angle made between walls and ceiling. Let us recall the definitions studied in the previous classes which are related to lines and angles.

Some Definitions

Line – The combination of many points which are arranged in a flow with almost negligible width and depth is called the Line. The line has no endpoint so it can be increased in both directions. Line AB is denoted by . Sometimes we use small letters like l, m, and n to denote lines.

Line Segment – The fixed portion of a line that has two endpoints and cannot be increased in any direction is called the Line Segment. If AB is a line segment, then it will be represented by .

Ray – The part of a line that has one endpoint and can be increased in one direction is called the Ray. If AB is a ray, then it will be denoted by .

Note – Sometimes we do not use the symbols for line, line segment, and ray. We generally write AB for all three.

Collinear Points – If three or more than three points lie on the same line, they are called Collinear Points.

Non-collinear Points – If three or more points do not lie on the same line, they are called Non-collinear Points.

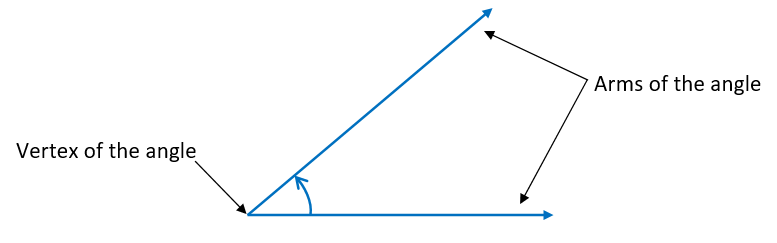
Angle – The inclination between two rays when they are originated from the same point is called an Angle. The two rays are called Arms of the angle and the common point is called Vertex of the angle. In the previous classes, we have studied different types of angles such as acute angle, right angle, obtuse angle, straight angle, and reflex angle.

Types of Angles

(i) Acute Angle – The angle which measures greater than 0° and less than 90° is called an acute angle. We can also say that an acute angle measures between 0° and 90°.

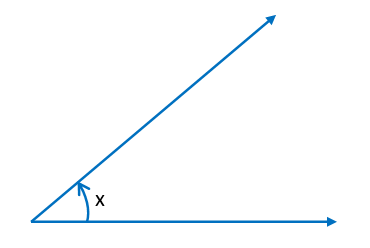
Here, the Acute angle: 0° < x < 90°

(ii) Right Angle – The angle which measures equal to 90° is called a right angle. We can also say that angle of 90° is a right angle.

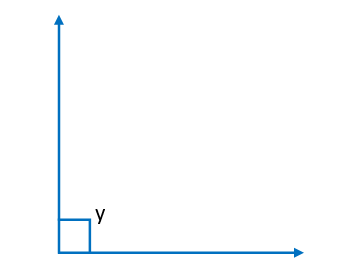
Here, the Right angle: y = 90°

(iii) Obtuse Angle ­­– The angle which measures greater than 90° and less than 180° is called an obtuse angle. We can also say that an obtuse angle measures between 90° and 180°.

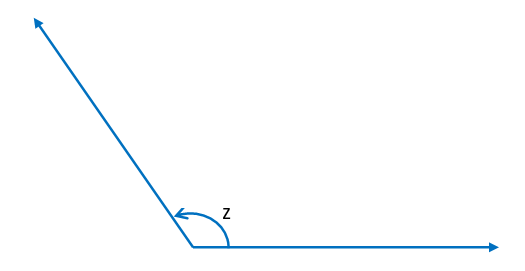
Here, the Obtuse angle: 90° < z < 180°

(iv) Straight Angle – The angle which measures equal to 180° is called a straight angle. We can also say that angle of 180° is a straight angle.

Here, the Straight angle: p = 180°

(v) Reflex Angle – The angle which measures greater than 180° and less than 360° is called a reflex angle. We can also say that a reflex angle measures between 180° and 360°.

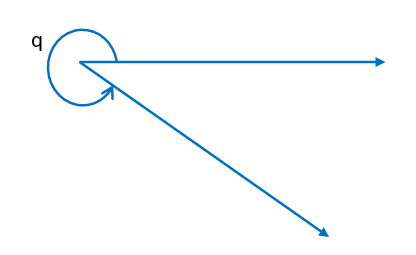
Here, the Reflex angle: 180° < q < 360°

(vi) Complementary Angles – When the sum of two angles is 90°, they are called complementary angles.

Example – (1) Complementary angle of 30° = 60° (⸪ 30° + 60° = 90°)

(2) Complementary angle of 50° = 40° (⸪ 50° + 40° = 90°)

(vii) Supplementary Angles – When the sum of two angles is 180°, they are called supplementary angles.

Example – (1) Supplementary angle of 125° = 55° (⸪ 125° + 55° = 180°)

(2) Supplementary angle of 95° = 85° (⸪ 95° + 85° = 180°)

(viii) Adjacent Angles – When two angles have a common vertex and a common arm, they are called adjacent angles. Their non-common arms are on different sides of the common arm.

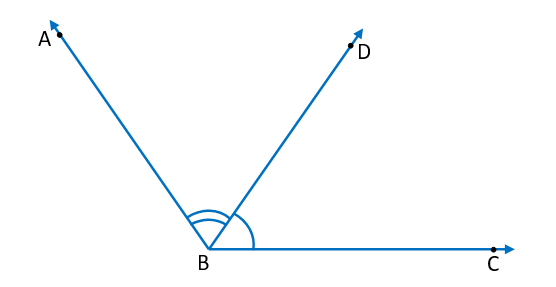
In the above figure, ∠ABD and ∠DBC are adjacent angles. Point B is their common vertex and ray BD is their common arm. Ray BA and BC are non-common arms.

We can also say that when two angles are adjacent angles, then their sum is always equal to the angle formed by the two non-common arms. So, for the above figure, we can write,

∠ABC = ∠ABD + ∠DBC

Note – ∠ABC and ∠DBC are not adjacent angles because their non-common arms AB and DB lie on the same side of the common arm BC. Similarly, ∠ABC and ∠ABD are also not adjacent angles.

(ix) Linear Pair of Angles – When the sum of the adjacent angles is 180° then they form a linear pair of angles or we can also say if the non-common arms of the adjacent angles form a straight line, then they are called a linear pair of angles.

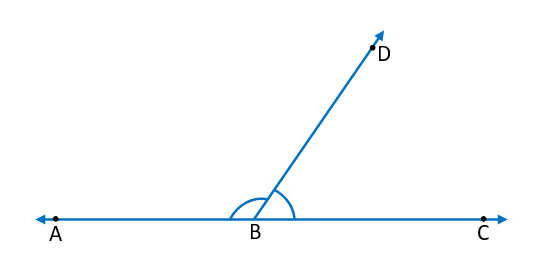
In the above figure, ∠ABD and ∠DBC are adjacent angles and their non-common arms AB and BC form a straight-line AC. It means the sum of angles ∠ABD and ∠DBC is 180°. Therefore, they are a linear pair of angles.

(x) Vertically Opposite Angles – When two lines intersect each other at a point, then angles made at the intersecting point are called vertically opposite angles.

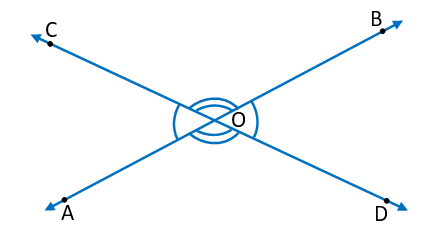
In the above figure, lines AB and CD intersect each other at point O. There are two pairs of vertically opposite angles. One pair is ∠AOD and ∠BOC and the other pair is ∠AOC and ∠BOD. Vertically opposite angles are always equal. Therefore,

∠AOD = ∠BOC

∠AOC = ∠BOD

Intersecting Lines and Non-intersecting (Parallel) Lines

Intersecting Lines – When two lines intersect each other at any point they are called intersecting lines. The distance between two intersecting lines is different at every point.

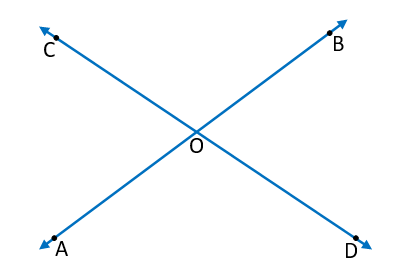
Lines AB and CD are intersecting lines and point O is the intersecting point.

Non-intersecting (Parallel) Lines – When two lines do not intersect each other at any point they are called non-intersecting (Parallel) lines. The distance between two parallel lines is equal at every point. The distance between two parallel lines is a perpendicular distance.

Lines AB and CD are parallel lines. For parallel lines, we write AB ∥ CD.

Pair of Angles

Vertically Opposite Angles

Parallel Lines and a Transversal

Lines Parallel to the Same Line

Angle Sum Property of a Triangle

Lines and Angles Class 9^th in Hindi

More About Lines and Angles