Decimal Numbers Class 7th

Introduction

Definition – In the number system, a Decimal is represented by a dot or point. The numbers which contain a dot or a point are called Decimal Numbers. In class 7^th, we shall study different operations and properties of decimal numbers.

Examples – 12.34, 3.789, 0.2561, 1679.098, etc.

We have already studied how can decimal be placed in any number. With the help of the place value table, let’s recall it.

Hundreds (100)	Tens (10)	Ones (1)	Tenths (1/10)	Hundredths (1/100)	Thousandths (1/1000)	Ten Thousandths (1/10000)	Number
7	5	3	8	2	1	6	753.8216
0	2	6	0	3	9	1	26.0391
7	7	8	9	0	0	5	778.9005
1	0	0	5	8	1	1	100.5811
0	0	9	0	0	0	4	9.0004

From the examples given in the above place value table, we can understand how we place decimals in numbers. The place value of the digit shows where the decimal will be placed. We can see that we place the decimal between the ones and the tenths place.

If we write the above examples in the expanded form then we can understand them clearly.

753.8216 = 7×100 + 5×10 + 3×1 + 8×(1/10) + 2×(1/100) + 1×(1/1000) + 6×(1/10000)

= 700 + 50 + 3 + 0.8 + 0.02 + 0.001 + 0.0006

= 753 + 0.8216 = 753.8216

In the above example, we read the decimal number as seven hundred fifty-three point eight two one six or seven hundred fifty-three decimal eight two one six. After the decimal, we read individual digits.

Some Important Points

1) In the division process, sometimes we get decimal numbers if the number is not completely divisible.

Examples – (1) 10 ÷ 4 = 2.5 (2) 250 ÷ 3 = 83.33

2) When we convert a smaller unit into a greater unit then we get a decimal number.

Example – (1) convert 50 meters into kilometers

Solution – we know that 1 km = 1000 m

50/1000 km = 0.050 km            Ans.

Example – (2) how many rupees are there in 325 paise?

Solution – since 1 rupee = 100 paise

Therefore, 325/100 rupees = 3.25 rupees             Ans.

Comparison, Addition, and Subtraction of Decimal Numbers

In the Comparison of Decimal numbers, first, we compare the digits of the left side of the decimal, if the digits are the same then we compare the digits of the right side of the decimal. We take an example.

Example – Compare 746.236 and 746.195

Solution – On the left side of the decimal, all three digits are the same. On the right side of the decimal, the digits at the tenths place are not the same so we compare these two digits.

Here, 2 > 1

So, 746.236 > 746.195              Ans.

Note – If the digits at the tenths place are also the same then we compare digits at the hundredths place and so on.

In the Addition of Decimal numbers, we add the numbers as simple addition. Only the place of decimal has to be taken into notice. When we write numbers, we put the decimal point below the decimal and then add. Let’s understand this with an example.

Example – Siddhi has two cakes each weighing 896.341 grams and 201.98 grams. Find the total weight of both cakes.

Solution –

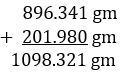
Total weight of both cakes = 1098.321 gm             Ans.

In the Subtraction of Decimal numbers, we subtract the same as addition. Let’s make it clear with an example.

Example – Lavanya has two school bags of cost 525.50 rupees and 450.75 rupees. Find the difference in the cost of both school bags.

Solution –

The difference in the cost of both school bags = 074.75 rupees              Ans.

Multiplication of Decimal Numbers

Multiplication of a Decimal Number by Another Decimal Number

The multiplication of two decimal numbers is the same as the multiplication of two whole numbers. When we multiply two decimal numbers, we can ignore the decimal for a moment and multiply them as whole numbers. After the complete multiplication, we place the decimal in the answer. How shall we place the decimal? Let’s understand with the help of an example.

Example – 1) Multiply 6.3 and 1.2.

Solution –

In this example, the number of digits after the decimal in both the numbers 6.3 and 1.2 is 1 and 1 so, in the answer, the digits after the decimal will be 2(1+1). Therefore, we place the decimal before the digits 56.

Example – 2) Multiply 45.34 and 2.7.

Solution –

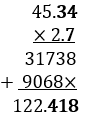
The number of digits after decimal in 45.34 and 2.7 = 2 and 1.

So, in the answer, the number of digits after the decimal will be 3(2+1).

Therefore, we place the decimal before the digits 418.

Multiplication of a Decimal Number by a Whole Number

This multiplication is the same as the above multiplication. In this multiplication, we place the decimal in the answer according to the decimal of the decimal number because another number is a whole number.

Example – Nainish has 3 ropes of each length of 7.5 m. what is the length of all the 3 ropes?

Solution – length of all the 3 ropes will be the multiplication of 3 with each length.

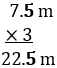
So, the length of all the 3 ropes is 22.5 m.              Ans.

In this example, the decimal number is 7.5, and the number of digits after the decimal is one. So, in the answer, the number of digits after the decimal will be also one. Therefore, we place the decimal before the digit 5.

Multiplication of a Decimal Number by Multiple of 10 (10, 100, 1000)

When a decimal number is multiplied by a multiple of 10 like 10, 100, 1000, 10000, and so on, the decimal is shifted to the right side on the basis of the number of 0’s. The example will help you to understand it better.

Example – Multiply 9.7614 by 10, 100, and 1000.

Solution – 9.7614×10 = 97.614

9.7614×100 = 976.14

9.7614×1000 = 9761.4                Ans.

When we multiply a decimal number by 10, the decimal is shifted one digit to the right side because the number of 0’s in 10 is one.

9.7614×10 = 97.614

When we multiply a decimal number by 100, the decimal is shifted two digits to the right side because the number of 0’s in 100 is two.

9.7614×100 = 976.14

When we multiply a decimal number by 1000, the decimal is shifted three digits to the right side because the number of 0’s in 1000 is three.

9.7614×1000 = 9761.4

Note – If the decimal number does not have sufficient digits to shift the decimal, then we use 0 as the digits. Example – 3.27×1000 = 3270.0

Division of Decimal Numbers

Division of a Decimal Number by Multiple of 10 (10, 100, 1000)

When we divide a decimal number by a multiple of 10 like 10, 100, 1000, 10000, and so on, the decimal is shifted to the left side on the basis of the number of 0’s. let’s take an example.

Example – Divide 3427.29 by 10, 100, and 1000.

Solution – 3427.29 ÷ 10 = 342.729

3427.29 ÷ 100 = 34.2729

3427.29 ÷ 1000 = 3.42729               Ans.

When we divide a decimal number by 10, the decimal is shifted one digit to the left side because the number of 0’s in 10 is one.

3427.29 ÷ 10 = 342.729

When we divide a decimal number by 100, the decimal is shifted two digits to the left side because the number of 0’s in 100 is two.

3427.29 ÷ 100 = 34.2729

When we divide a decimal number by 1000, the decimal is shifted three digits to the left side because the number of 0’s in 1000 is three.

3427.29 ÷ 1000 = 3.42729

Note – If the decimal number does not have sufficient digits to shift the decimal, then we use 0 as the digits. Example – 99.35 ÷ 1000 = 0.09935

Division of a Decimal Number by a Whole Number

In the division of a decimal number by a whole number, we convert a decimal number into a fraction and the division sign into multiplication and write the reciprocal of a whole number, and then multiply.

Example – Divide 55.2 by 4

Solution – 55.2 ÷ 4 = (552/10) × ¼ = 552/10×4 = 138/10 = 13.8           Ans.

Note – We convert the decimal numbers into fractions by removing the decimal. In the place of the decimal, we write 1 in the denominator, and on the basis of the number of digits after the decimal, we write 0’s in the denominator. Example – 16.25 = 1625/100

Division of a Whole Number by a Decimal Number

Same as the above division, we convert a decimal number into a fraction and the division sign into multiplication. Then we write the reciprocal of the fraction and multiply.

Example – Divide 35 by 0.5.

Solution – 35 ÷ 0.5 = 35 ÷ 5/10 = 35×10/5 = 7×10 = 70            Ans.

Note – If we have to convert the decimal number into a fraction and the decimal number is written in the denominator then in the place of the decimal, we write 1 in the numerator, and on the basis of the number of digits after the decimal, we write 0’s in the numerator. Example – 1/16.25 = 100/1625.

Division of a Decimal Number by Another Decimal Number

In the division of a decimal number by another decimal number, first, we convert both decimal numbers into fractions. After that, we convert the sign of division into multiplication and write the reciprocal of the divisor fraction, and then multiply.

Example – Divide 40.5 by 0.15.

Solution – 40.5 ÷ 0.15

405/10 ÷ 15/100 = (405/10) × (100/15) = 4050/15 = 270         Ans.

Note – In the division of decimal numbers, If the number of digits after the decimal is equal in both the numbers then we can divide those numbers as whole numbers by ignoring the decimal. Example – 3.6 ÷ 1.2 = 36/12 = 3.

Decimal Numbers Class 7^th in Hindi

More About Decimal Numbers