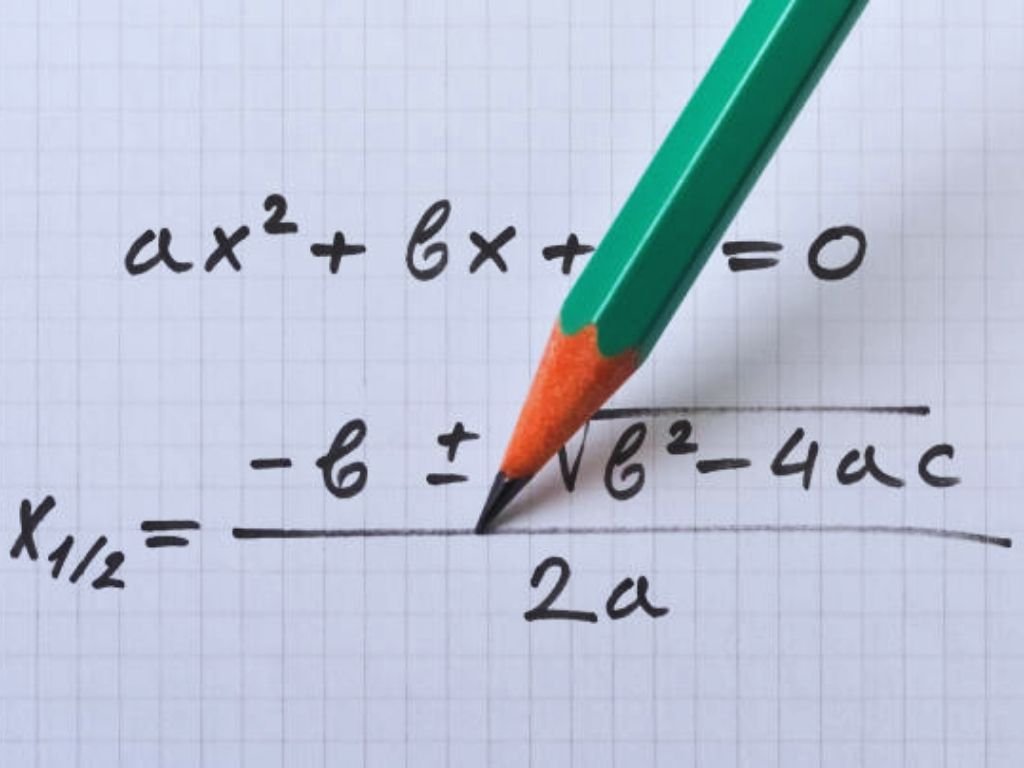Solving Polynomials
Introduction
To solve a polynomial, we put that polynomial equals zero (0) and find the value of the variable in it. Values of the variable are called zeroes or roots of the polynomial which depend on the degree of the polynomial. if the degree of the polynomial is 1 then there will be one zero or root and if the degree is 2 then there will be two zeroes or roots.
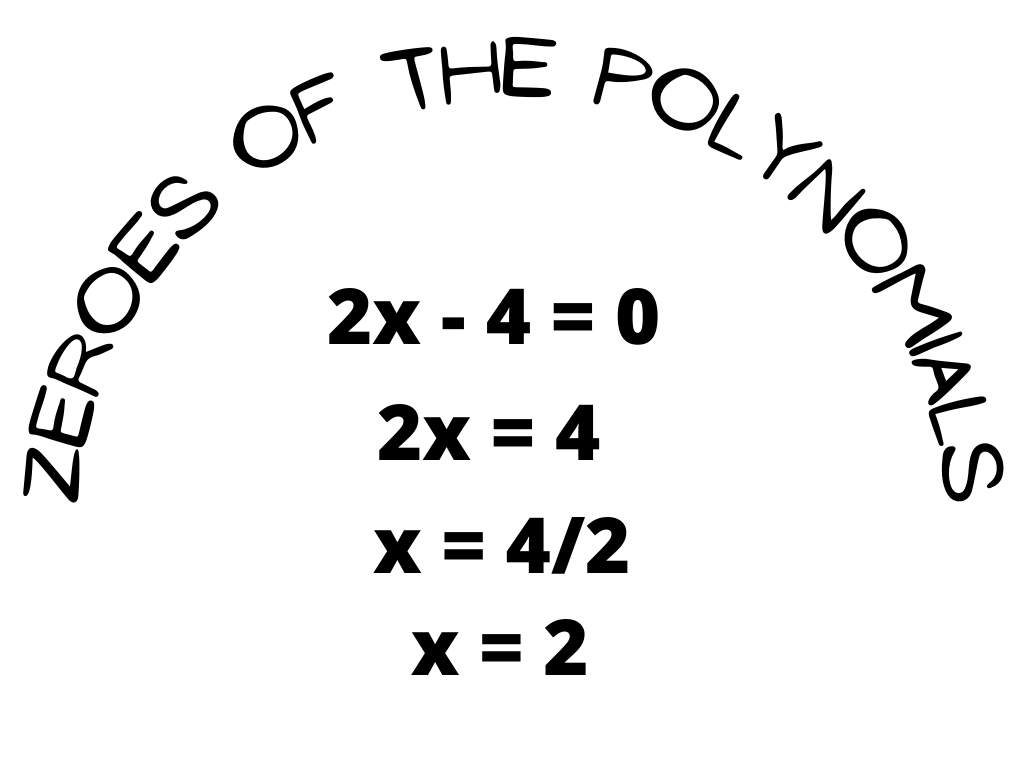
- Solving a linear polynomial
- Solving a quadratic polynomial
- Solving a cubic polynomial
Solving a Linear Polynomial
In the linear polynomial, the degree is always 1 so there will be one and only one zero. if the linear polynomial is p(x) then to find the zero of the polynomial p(x) we have to solve the equation p(x) = 0.
Examples
Example – 1) find the zero of the polynomial p(x) = 3x + 2.
Solution – let p(x) = 0
3x + 2 = 0
3x = – 2
x = -2/3
x = -2/3 is the zero of the polynomial p(x) = 3x + 2. Ans.
Example – 2) find the zero of the polynomial p(y) = 2y – 6.
Solution – let p(y) = 0
2y – 6 = 0
2y = 6
y = 6/2
y = 3
Zero of the polynomial p(y) = 2y – 6 is y = 3. Ans.
Note – Standard form of the linear polynomial is ax + b = 0 where a ≠ 0 so the zero will be x = -b/a. we can also find the zero by comparing it.
Solving a Quadratic Polynomial
In the quadratic polynomial, the degree is 2 so there will be two zeroes.
Examples
Example – 1) find the zeroes of the polynomial x2 – 3x.
Solution – let p(x) = x2 – 3x
Now P(x) = 0
x2 – 3x = 0
x(x – 3) = 0
x = 0 and x – 3 = 0
x = 0 and x = 3
The two zeroes are x = 0 and x = 3. Ans.
Example – 2) find the zeroes of the polynomial 6x2 + 5x – 6.
Solution – let p(x) = 6x2 + 5x – 6
Now p(x) = 0
6x2 + 5x – 6 = 0
6x2 + 9x – 4x – 6 = 0 (By factorization method) [9−4 = 5 and 9⨯(-4) = -36]
3x(2x+3) – 2(2x+3) = 0
(2x + 3)(3x – 2) = 0
2x + 3 = 0 and 3x – 2 = 0
2x = -3 and 3x = 2
x = -3/2 and x = 2/3
These are the zeroes of the given polynomial. Ans.
Solving a Cubic Polynomial
In the cubic polynomial, the degree is 3 so there will be three zeroes. To solve the cubic polynomial first we have to arrange the polynomial in descending order then we solve it by taking common terms or by factorization.
Examples
Example – 1) find the zeroes of the polynomial x3 + 2x2 – x – 2.
Solution – let p(x) = x3 + 2x2 – x – 2
Now p(x) = 0
x3 + 2x2 – x – 2 = 0
x2(x + 2) – 1(x + 2) = 0
(x + 2)(x2 – 1) = 0
x + 2 = 0 and x2 – 1 = 0
x = -2 and x2 = 1
x = ±√1
x = ±1
So, the zeroes are x = -2, x = +1, and x = -1. Ans.
Note – We can check the answer by putting the value of each zero in the given polynomial because, at each value of zero, the value of the polynomial is 0.
Example – 2) find the zeroes of the polynomial x3 + 6x2 + 11x + 6.
Solution – let p(x) = x3 + 6x2 + 11x + 6
There is not any common term in it.
So, the factors of the constant term 6 = ±1, ±2, ±3 and ±6
Now at x = +1
p(1) = (1)3 + 6(1)2 + 11(1) + 6
p(1) = 1 + 6 + 11 + 6
p(1) = 24
∵ p(1) ≠ 0 so x = +1 is not the zero of this polynomial.
Here, all the terms in the polynomial are positive so we shall take only negative factors.
Now at x = – 1
p(-1) = (-1)3 + 6(-1)2 + 11(-1) + 6
p(-1) = -1 + 6 – 11 + 6
p(-1) = 0
∵ p(-1) = 0 so x = -1 is the zero of this polynomial.
Now at x = -2
p(-2) = (-2)3 + 6(-2)2 + 11(-2) + 6
p(-2) = – 8 + 6(4) – 22 + 6
p(-2) = – 8 + 24 – 22 + 6
p(-2) = 0
∵ p(-2) = 0 so x = -2 is the zero of this polynomial.
Now at x = -3
p(-3) = (-3)3 + 6(-3)2 + 11(-3) + 6
p(-3) = -27 + 6(9) – 33 + 6
p(-3) = -27 + 54 – 33 + 6
p(-3) = 0
∵ p(-3) = 0 so x = -3 is the zero of this polynomial.
∵ The degree of the given polynomial is 3 so there will be only three zeroes.
So, the zeroes of the given polynomial are x = -1, x = -2, and x = -3. Ans.