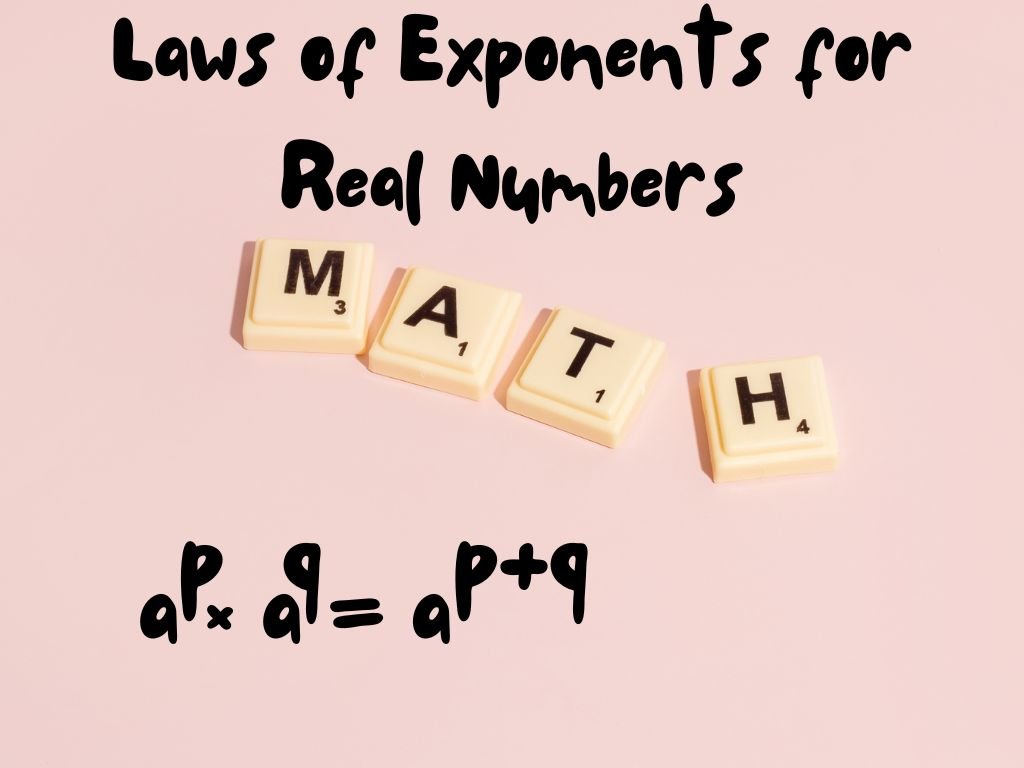Powers and Exponents Class 8th

Introduction

In the previous class, we have already studied powers and exponents. We know that exponents are used to write large numbers in a suitable and convenient form. In large calculations, powers and exponents are very important and useful. In class 8th, we shall explore more about powers and exponents with the help of their laws, comparison, use, and examples.

For example – 1260000000000 is a very large number. We can write this number using an exponent like 1.26×10¹². In this number, we read 10¹² as ten (10) raised to the power twelve (12). In 10¹², number 10 is called Base, and number 12 is called Exponent. The place where the exponent is written is called Power.

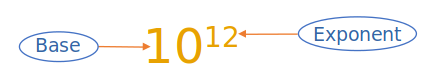
Numbers with Negative Exponents in Power

Generally, we write positive exponents in the power of a number. If the exponent is negative then how can we solve these types of exponents? Let us understand with the help of some examples.

Example – 1) What is the value of 5^-2?

Solution – we can write 5^-2 = 1/5² = 1/25 Ans.

To solve negative exponents we move the exponent to the denominator if the exponent is in the numerator and if the exponent is in the denominator, we move that to the numerator. By doing this the negative exponent turns into a positive exponent.

Example – 2) Solve 1/10^-3, 10^-5, 1/8^-4.

Solution – 1/10^-3 = 10³

10^-5 = 1/10⁵

1/8^-4 = 8⁴ Ans.

Example – 3) Convert 10⁶, 1/3⁹, 7² into negative exponents.

Solution – 10⁶ = 1/10^-6

1/3⁹ = 3^-9

7² = 1/7^-2 Ans.

Note – from the above examples, we can say that if there is a positive exponent a^m then its negative exponent is 1/a^-m or we can say that a^m = 1/a^-m. Where a is a non-zero integer. a^m is the multiplicative inverse of a^-m.

Laws of Exponents

To solve exponents there are some laws that are very useful. Let there be two non-zero integers a and b and two integers m and n to verify the laws of exponents which are given below.

1) a^m × aⁿ = a^m+n

2) a^m / aⁿ or a^m ÷ aⁿ = a^{m – n}

3) a^m × b^m = (ab)^m

4) a^m / b^m or a^m ÷ b^m = (a/b)^m

5) (a^m)ⁿ = a^mn

6) a⁰ = 1

7) if a^m = aⁿ then m = n

Note – 1) According to law a⁰ = 1

Let’s prove this law, LHS = a⁰

= a^{1 – 1} (since 1 – 1 = 0)

= a^{1 + (-1)}

= a¹ × a^-1 (using the reverse order of the law a^m × aⁿ = a^m+n)

= a¹ / a¹

= 1

= RHS

2) All the above laws are also used for negative exponents which we shall understand with the help of examples.

Some Examples –

Example 1) Solve 3⁵ × 3³

Solution – using the law a^m × aⁿ = a^m+n

3⁵ × 3³ = 3⁵⁺³ = 3⁸ Ans.

Example 2) Find the value in exponential form.

(1) 6^-2 × 6⁷ (2) (-9)⁴ × 2⁴

Solution – 1) 6^-2 × 6⁷

using the law a^m × aⁿ = a^m+n

6^-2 × 6⁷ = 6^-2+7 = 6⁵ Ans.

2) (-9)⁴ × 2⁴

using the law a^m × b^m = (ab)^m

(-9)⁴ × 2⁴ = (-9 × 2)⁴ = (-18)⁴ Ans.

Example 3) Simplify 2^-1 / 2³

Solution – using the law a^m / aⁿ or a^m ÷ aⁿ = a^{m – n}

2^-1 / 2³ = 2^-1-3 = 2^-4 = 1/2⁴ Ans.

Use of Exponents

To Express Small Numbers in Standard Form

To Express Large Numbers in Standard Form

Comparison of Very Small and Very Large Numbers

Examples

Powers and Exponents Class 8^th in Hindi

More About Powers and Exponents