Introduction
Quadratic Formula (Shridharacharya Sutra) – The quadratic formula is given by the great Indian mathematician Shridharacharya and is also known as Shridharacharya Sutra. This formula is used to solve the quadratic equation.
x = –b ± √(b2 – 4ac)/2a
Where, x = variable
a, b, c = Coefficients of quadratic equation
Derivation of Formula
↣ This formula can be derived from the perfect square method.
The standard form of a quadratic equation is
ax2 + bx + c = 0
x2 + bx/a + c/a = 0 (taking 1 as coefficient of x2 or dividing the whole equation by the coefficient of x2 (a))
x2 + bx/a = −c/a (taking the constant term to the right side)
x2 + bx/a + (b/2a)2 = −c/a + (b/2a)2 (adding square of half of coefficient of x)
(x + b/2a)2 = −c/a + b2/4a2
(x + b/2a)2 = (−c⨯4a + b2⨯1)/4a2 = (−4ac + b2)/4a2
Taking square root on both sides,
√(x + b/2a)2 = √(−4ac + b2)/4a2
x + b/2a = ±√(b2 − 4ac)/2a
x = −b/2a ± √(b2 − 4ac)/2a
x = −b ± √(b2 − 4ac)/2a
Here sign ± shows the two values of x.
x = −b + √(b2 − 4ac)/2a x = −b − √(b2 − 4ac)/2a
The above values of x are the Quadratic Formula (Shridharacharya sutra).
Example – Solve the quadratic equation 9x2 + 7x – 2 = 0 by Shridharacharya sutra.
Solution – given equation 9x2 + 7x – 2 = 0
Comparing with standard form ax2 + bx + c = 0
So, a = 9, b = 7, c = – 2
By quadratic formula, x = −b ± √(b2 − 4ac)/2a
Putting the values of a, b, c
x = −7 ± √{72 − 4⨯9⨯(-2)}/2⨯9
x = −7 ± √{49 + 72}/18
x = −7 ± √{121}/18 = −7 ± 11/18
On taking the (+) sign,
x = −7 + 11/18
x = 4/18
x = 2/9
On taking the (−) sign,
x = −7 − 11/18
x = −18/18
x = −1
These values of x are the roots of the given quadratic equation. Ans.
Discriminant and Nature of Roots
We can find the nature of roots by the term b2 – 4ac used in the Shridharacharya sutra which is called the Discriminant. It is denoted by D.
D = b2 – 4ac
⇒ If D > 0 then the roots will be different and real.
x = (−b + √D)/2a and x = (−b − √D)/2a
⇒ If D = 0 then the roots will be equal and real.
x = −b/2a and x = −b/2a
⇒ If D < 0 then the roots will not be real, they will be imaginary.
Some Examples –
Example – 1) find the nature of the roots of equation 2x2 – 6x + 3 = 0 and if roots exist then find them.
Solution – Given equation 2x2 – 6x + 3 = 0
Comparing the equation with ax2 + bx + c = 0
Here, a = 2, b = – 6, c = 3
Now D = b2 – 4ac
D = (-6)2 – 4⨯2⨯3 = 36 – 24 = 12
∵ D > 0
∴ The roots of equation 2x2 – 6x + 3 = 0 will be different and Real.
By Shridharacharya formula, x = (−b ± √D)/2a where, D = b2 – 4ac
x = {−(-6) ± √12)}/2⨯2 = {6 ± √(4⨯3)}/4
x = {6 ± 2√3}/4 = 2{3 ± √3}/4 = {3 ± √3}/2
So, the roots are x = (3 + √3)/2 and x = (3 − √3)/2. Ans.
Example – 2) find the nature of roots of the equation x2 – 4x + 4 = 0 and if roots exist then find them.
Solution – Given equation x2 – 4x + 4 = 0
By comparing with ax2 + bx + c = 0
a = 1, b = – 4, c = 4
Now, D = b2 – 4ac
D = (-4)2 – 4⨯1⨯4 = 16 – 16 = 0
∵ D = 0
∴ The roots of the equation x2 – 4x + 4 = 0 will be equal and Real.
By quadratic formula, x = (−b ± √D)/2a where, D = b2 – 4ac
x = {−(-4) ± √0)/2⨯1 = (4 ± 0)/2 = 4/2
x = 2
So, the roots are x = 2 and x = 2. Ans.
Example – 3) find the nature of the roots of equation 2x2 + 3x + 5 = 0 and if roots exist then find them.
Solution – Given equation 2x2 + 3x + 5 = 0
On comparing with ax2 + bx + c = 0
a = 2, b = 3, c = 5
Now D = b2 – 4ac
D = (3)2 – 4⨯2⨯5 = 9 – 40 = –31
∵ D < 0
∴ The roots of equation 2x2 + 3x + 5 = 0 will not be Real. They will be imaginary.
By Shridharacharya quadratic formula, x = (−b ± √D)/2a where, D = b2 – 4ac
x = (−3 ± √-31)/2⨯2 = (−3 ± √−1⨯31)/4
x = (−3 ± √−1⨯√31)/4 = (−3 ± √31i )/4
So, the roots x = (−3 + √31i )/4 and x = (−3 − √31i )/4. where, i(iota) = √−1
Quadratic Formula (Shridharacharya Sutra) Class 10th in Hindi
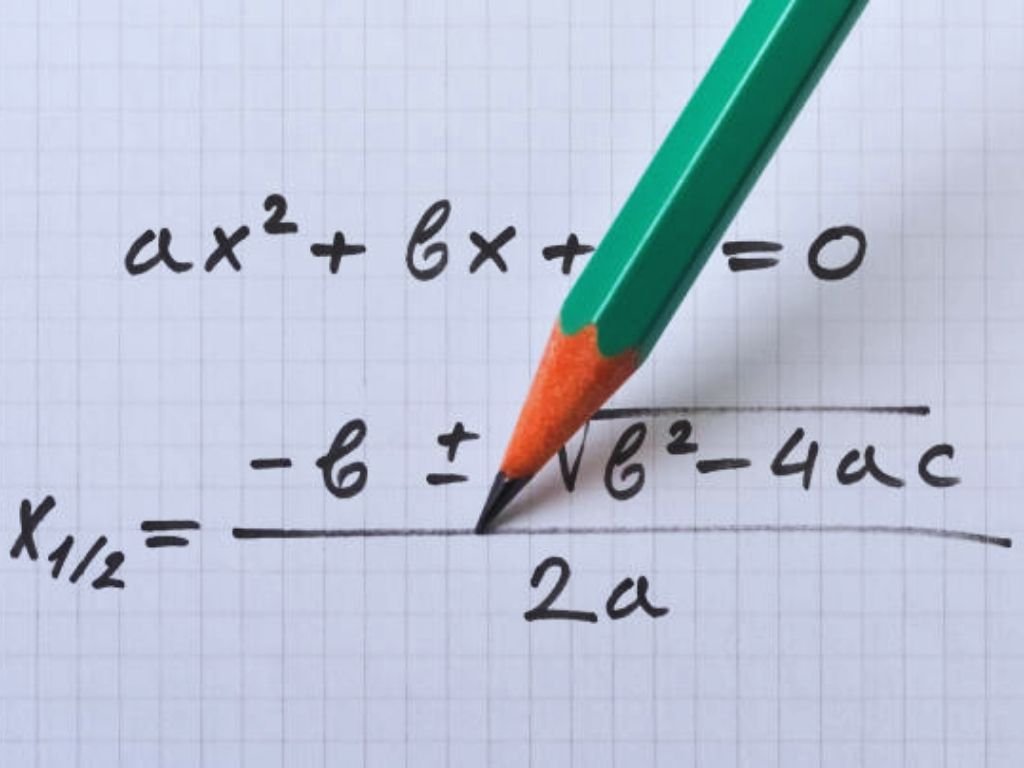
Perfect blog, This blog is good for class 10 math students. It’s also have quadratic formulas.
Thank You