Pair of Linear Equations in Two Variables Class 10th

We are familiar with linear equations in two variables as we have studied them in previous classes. The linear equation having two variables is called the linear equation in two variables. In class 10^th, we shall study the pair of linear equations in two variables, the solution of a pair of linear equations in two variables by graphical method and algebraic methods.

Pair of Linear Equations in Two Variables

The standard form of linear equations in two variables is ax + by + c = 0, where a, b, and c are real numbers and a, b ≠ 0 (we often denote a, b ≠ 0 by a² + b² ≠ 0). The equation which can be written in the form ax + by + c = 0 is called a linear equation in two variables x and y. some examples of linear equations in two variables are as follows.

2x + 5y + 9 = 0

x – 3y = 8

4x – y – 10 = 0

x + y = 0

7x = 6 or 7x – 0y = 6

In the pair of linear equations in two variables, there are two linear equations. We know that the solution of linear equations in two variables is a pair of values, one for x and the other for y. Both the values of x and y satisfy the respective linear equation.

In a pair of linear equations in two variables, there will be two pairs of values, one pair for each equation.

For example, if we substitute x = -2 and y = -1 in the left-hand side (LHS) of equation 2x + 5y + 9 = 0. Then

LHS = 2x + 5y + 9 = 2(-2) + 5(-1) + 9 = – 4 + (-5) + 9 = – 4 – 5 + 9 = – 9 + 9 = 0

RHS = 0

0 = 0

LHS = RHS

We can see LHS is equal to the RHS of the equation. Therefore, x = -2 and y = -1 is a solution of equation 2x + 5y + 9 = 0.

Now if we substitute x = 1 and y = 1 in the equation 2x + 5y + 9 = 0. Then

LHS = 2(1) + 5(1) + 9 = 2 + 5 + 9 = 16

LHS is not equal to the RHS of the equation. Therefore, x =1 and y = 1 is not a solution of equation 2x + 5y + 9= 0.

Geometrically, the point x = -2 and y = -1 or (-2, -1) lies on the line representing the equation 2x + 5y + 9= 0 because it is a solution of this equation and the point (1, 1) does not lie on this line because it is not a solution of this equation.

Therefore, every solution of the linear equation is a point that lies on the line representing it.

In general, we can say that for any linear equation in two variables such as ax + by + c = 0, each solution (x, y) of this equation corresponds to a point that lies on the line representing the equation, and vice versa.

If two linear equations are in the same two variables like x and y then these types of equations are called a pair of linear equations in two variables.

The general form of a pair of linear equations in two variables x and y is given as follows.

a₁x + b₁y + c₁ = 0

a₂x + b₂y + c₂ = 0

Where a₁, b₁, c₁, a₂, b₂, c₂ are real numbers and a₁, b₁ ≠ 0 (a₁² + b₁² ≠ 0), a₂, b₂ ≠ 0 (a₂² + b₂² ≠ 0)

Some Examples –     x + 5y + 8 = 0 and 3x + 2y – 4 = 0

6x – y = 7 and 2x – 9y = 0

-x + y = 1 and 3x – 8 = 0

y = 4 and 2y + 5x = -2

We know that the graphical representation of a linear equation is a straight line and for a pair of linear equations in two variables, there will be two straight lines together. But how would they look geometrically?

Geometrically, if two straight lines are present together in a plane then there may be three possibilities.

{1} The two lines will intersect each other at one point.

{2} The two lines will not intersect each other, i.e., they will be parallel.

{3} The two lines will coincide with each other.

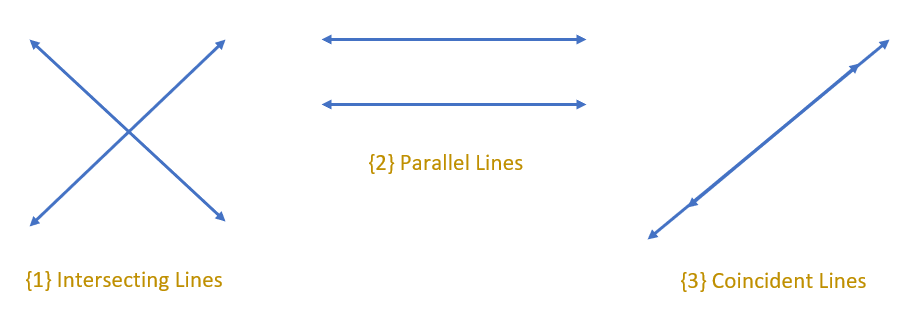
We can graphically represent a pair of linear equations as two straight lines and the lines may intersect, may be parallel, or may coincide as shown in the above figures.

Graphical Method to Solve a Pair of Linear Equations

How can we solve a pair of linear equations in two variables graphically? What will be the solution of a pair of linear equations in each case? Let’s answer these questions with the help of some examples.

Example {1} Solve the pair of linear equations graphically and check whether they are intersecting, parallel, or coincide.

2x + y = 4

x – 2y – 7 = 0

Solution – First of all we find the values of x and y from both equations. To find the values, we substitute any value of one variable and get the value of another variable. We make two tables, one for each equation.

2x + y = 4

y = 4 – 2x

x	0	1	2
y	4	2	0

x – 2y – 7 = 0

x = 7 + 2y

y	0	-1	-2
x	7	5	3

Now we plot the values of both tables one by one. First, we plot the values of the first table and after that the values of the second table.

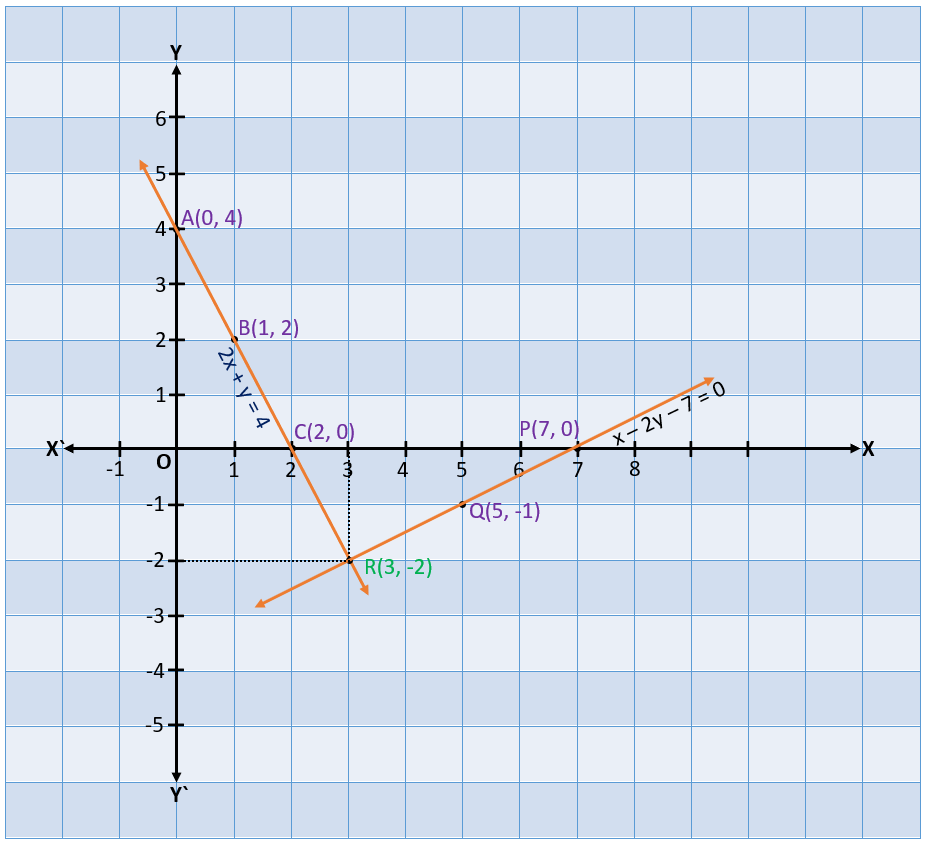
We plot the points A(0, 4), B(1, 2), C(2, 0) and P(7, 0), Q(5, -1), R(3, -2) from both tables. Now, we join points A, B, C, and P, Q, R. We get two lines which are representing the equations 2x + y = 4 and x – 2y – 7 = 0.

From the above graph, we can see that two lines representing two equations are intersecting each other at point R(3, -2). It means this is the common point on both lines. This shows that there is one and only one solution (unique solution) (x = 3 and y = -2) for this pair of linear equations in two variables.

We can also verify algebraically that x = 3 and y = -2 is the solution of the given pair of equations. Putting the values of x and y in each equation, we get

2x + y = 4

2×3 + (-2) = 4

6 – 2 = 4

4 = 4

LHS = RHS

x – 2y – 7 = 0

3 – 2×(-2) – 7 = 0

3 – (-4) – 7 = 0

3 + 4 – 7 = 0

7 – 7 = 0

0 = 0

LHS = RHS

We can see that x = 3 and y = -2 is satisfying both equations. Therefore, x = 3 and y = -2 is the solution of both the given equations.            Ans.

Example {2} Solve the pair of linear equations graphically and check whether they are intersecting, parallel, or coincide.

x + 2y = 5

2x + 4y = 10

Solution – First of all we find the values of x and y from both equations. To find the values, we substitute any value of one variable and get the value of another variable. We make two tables, one for each equation.

x + 2y = 5

x = 5 – 2y

y	0	1	2
x	5	3	1

2x + 4y = 10

x = 10 – 4y / 2

y	0	-1	2
x	5	7	1

Now we plot the values of both tables one by one. First, we plot the values of the first table and after that the values of the second table.

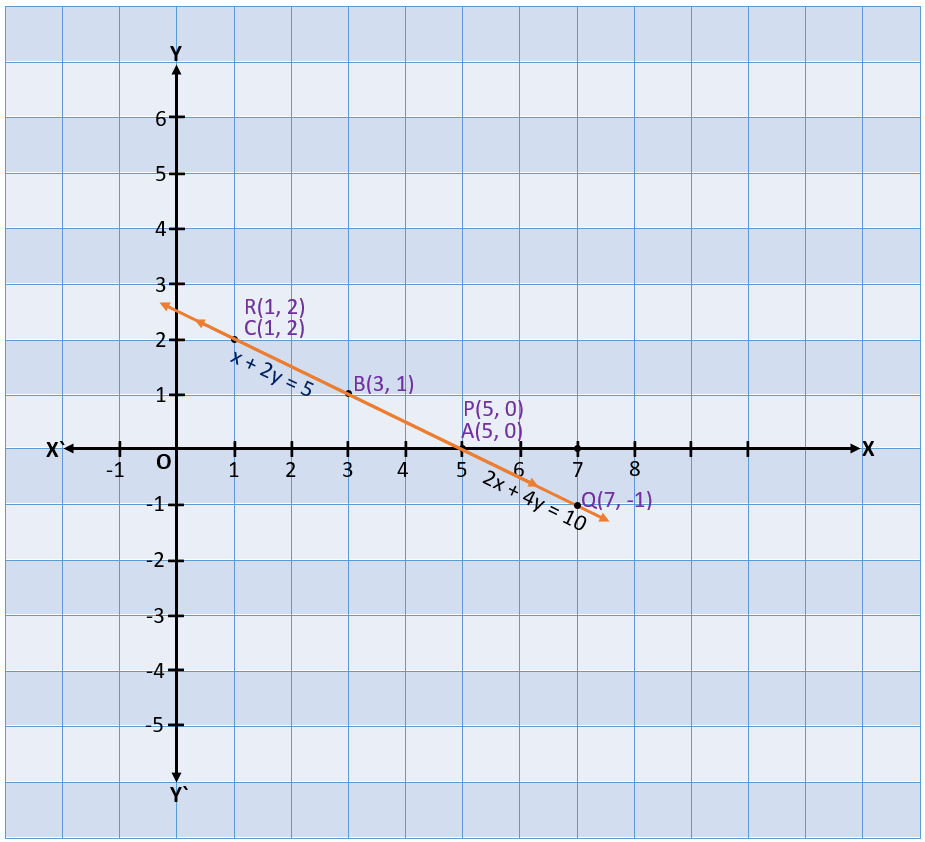
We plot the points A(5, 0), B(3, 1), C(1, 2) and P(5, 0), Q(7, -1), R(1, 2) from both tables. Now, we join points A, B, C and P, Q, R. We get two lines which are representing the equations x + 2y = 5 and 2x + 4y = 10.

From the above graph, we can see that two lines representing two equations are coinciding with each other. It means every point is the common point on both lines. This shows that there are infinitely many solutions for this pair of linear equations in two variables.

if we divide the second equation 2x + 4y = 10 by 2, we get x + 2y = 5, which is the same as first equation (x + 2y = 5). This shows that both equations are equivalent.

Example {3} Solve the pair of linear equations graphically and check whether they are intersecting, parallel, or coincide.

x + 3y = 5

2x + 6y = 12

Solution – First of all we find the values of x and y from both equations. To find the values, we substitute any value of one variable and get the value of another variable. We make two tables, one for each equation.

x + 3y = 5

x = 5 – 3y

y	0	1	2
x	5	2	-1

2x + 6y = 12

x = 12 – 6y / 2

y	0	1	2
x	6	3	0

Now we plot the values of both tables one by one. First, we plot the values of the first table and after that the values of the second table.

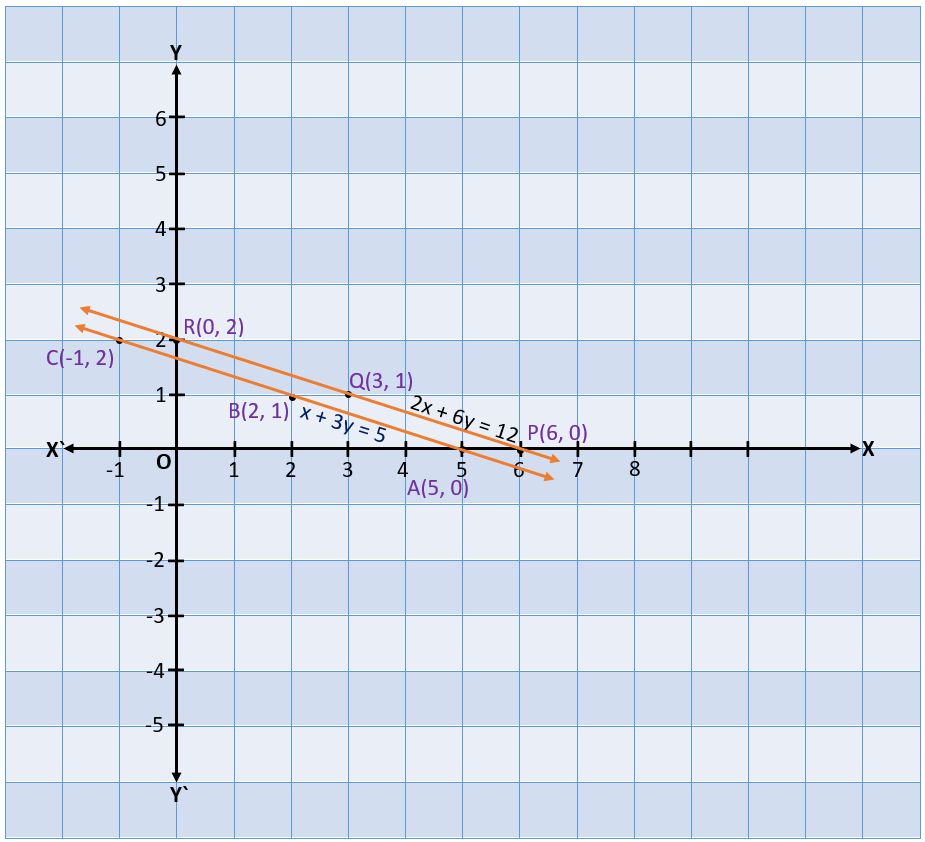
We plot the points A(5, 0), B(2, 1), C(-1, 2) and P(6, 0), Q(3, 1), R(0, 2) from both tables. Now, we join points A, B, C and P, Q, R. We get two lines which are representing the equations x + 3y = 5 and 2x + 6y = 12.

From the above graph, we can see that two lines representing two equations are parallel to each other. It means there is not any common point of both lines. This shows that there is no solution for this pair of linear equations in two variables.

Note – {1} A pair of linear equations in two variables, which has any solution, is called a consistent pair of linear equations.

{2} A pair of linear equations in two variables, which has not any solution, is called an inconsistent pair of linear equations.

{3} In example {1}, there is only one solution therefore the pair of linear equations is consistent. In example {2}, there are infinitely many solutions therefore the pair is dependent pair of linear equations and the dependent pair is always a consistent pair. In example {3}, there is not any solution therefore the pair of linear equations is inconsistent.

Now we compare the values of a₁/a₂, b₁/b₂, and c₁/c₂ in all the three examples solved above. Where a₁, b₁, c₁ and a₂, b₂, c₂ are the coefficients of the pair of linear equations in two variables. We make the following comparison table which helps us to find the behavior of a pair of linear equations.

Sr. No.	Pair of Linear Equations	a1/a2	b1/b2	c1/c2	Comparison of Ratios	Graphical Representation	Algebraic Interpretation	Behavior
1.	2x + y – 4 = 0 x – 2y – 7 = 0	2/1	1/-2	-4/-7	a1/a2 ≠ b1/b2	Intersecting Lines	Only One Solution (Unique Solution)	Consistent
2.	x + 2y – 5 = 0 2x + 4y – 10 = 0	1/2	2/4	-5/-10	a1/a2 = b1/b2 = c1/c2	Coincident Lines	Infinitely Many Solutions	Consistent
3.	x + 3y – 5 = 0 2x + 6y – 12 = 0	1/2	3/6	-5/-12	a1/a2 = b1/b2 ≠ c1/c2	Parallel Lines	No Solution	Inconsistent

Algebraic Methods to Solve a Pair of Linear Equations

{1} Substitution Method

{2} Elimination Method

{3} Cross-Multiplication Method

Different Forms of a Pair of Linear Equations in Two Variables

Pair of Linear Equations in Two Variables Class 10th in Hindi

More About Pair of Linear Equations in Two Variables