The variance is a widely used concept in probability and descriptive statistics for measuring the variability of the given data. The variance is a technique for determining the various terms in finance. It is just the same as the standard deviation but it is measured in squared units.
Let us explore the term variance.
What is the Variance in Statistics?
Variance can be defined as the statistical measure of the deviation between numbers in a dataset. The variance of a set measures how far each number is from the expected value (mean), as well as from the other numbers.
The result of the variance is the square of the standard deviation. The term standard deviation is another statistical technique that measures the average of the squared deviations. Symbolically, the term variance can be written as s2, σ2, or Var(x).
The data set in the variance could be population or sample. The sample data is a set of sample values taken from the whole population to measure the estimated value. Whereas the population data set is the set of a whole number of values such as the population taking the whole data.
There are two main kinds of variance:
- Sample Variance
- Population Variance
Formulas of Variance
The formulas for the sample and population variance are:
| For population variance | For sample variance |
| σ2 = [∑(xi – μ)2/N] | s2 = [∑(xi – x̄)2/(N – 1)] |
| > σ2 is the notation of population variance. > μ is the average value of the population data. > Xi is the set of given data values. > N is the total number of observations. | > s2 is the notation of sample variance. > x̄ is the average value of sample data. > Xi is the set of given data values. > N is the total number of observations. |
Advantages of Variance
There are some advantages and disadvantages of the variance. Let us discuss them briefly.
| Advantages |
| It is used to measure the relationship among the numbers and the average values to make work easier for statisticians as the other way is rather difficult such as arranging numbers into quartiles. |
| The deviations from the expected values are treated the same in the variance regardless of their direction. |
| There is no variability at all in data as the square of deviations can’t sum to zero. |
Properties of Variance
Some properties of the variance are:
1) The sum of the constant term with variance should skip constant terms such as:
Var(X + C) = Var(X)
2) The product of a constant term with variance should take out the square of the constant term. Such as
Var(C * X) = C2 * Var(X)
3) Similarly, the product and sum of a constant term with variance should take out the square of the constant term. Such as
Var(aX + b) = a2 * Var(X)
4) The variance should be applied to each term separately if the random variables X1, X2, …, Xn are given such as
Var(X1, X2, …, Xn) = Var(X1) + Var(X2) +……..+Var(Xn)
Examples of Variance
Below are a few examples of variance.
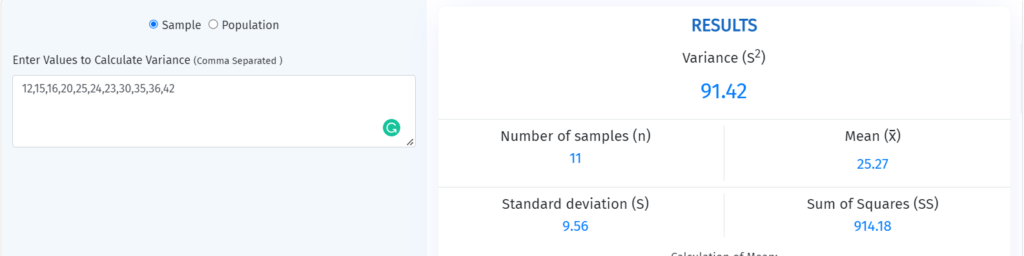
Example 1: For Sample Variance
Measure the variability in the given sample data.
Sample data = 12, 15, 16, 20, 25, 24, 23, 30, 35, 36, 42
Solution –
Step 1: First of all, find the sample average value by taking the quotient of the sum of observations and the total number of data values.
Sum of sample data = 12 + 15 + 16 + 20 + 25 + 24 + 23 + 30 + 35 + 36 + 42
Sum = 278
Total number of observation = N = 11
Sample Mean = 278/11
Sample Mean = 25.27
Step 2: Now find the deviation (difference of each data value from the average).
| Data values | zi – z̄ |
| 12 | 12 – 25.27 = -13.27 |
| 15 | 15 – 25.27 = -10.27 |
| 16 | 16 – 25.27 = -9.27 |
| 20 | 20 – 25.27 = -5.27 |
| 25 | 25 – 25.27 = -0.27 |
| 24 | 24 – 25.27 = -1.27 |
| 23 | 23 – 25.27 = -2.27 |
| 30 | 30 – 25.27 = 4.73 |
| 35 | 35 – 25.27 = 9.73 |
| 36 | 36 – 25.27 = 10.73 |
| 42 | 42 – 25.27 = 16.73 |
Step 3: Now take the square of the deviations to make all the results positive.
| (zi – z̄)2 |
| (-13.27)2 = 176.09 |
| (-10.27)2 = 105.47 |
| (-9.27)2 = 85.93 |
| (-5.27)2 = 27.77 |
| (-0.27)2 = 0.07 |
| (-1.27)2 = 1.61 |
| (-2.27)2 = 5.15 |
| (4.73)2 = 22.37 |
| (9.73)2 = 94.67 |
| (10.73)2 = 115.13 |
| (16.73)2 = 279.89 |
Step 4: Now take the sum of the squared deviations.
∑(zi – z̄)2 = 176.09 + 105.47 + 85.93 + 27.77 + 0.07 + 1.61 + 5.15 + 22.37 + 94.67 + 115.13 + 279.89
∑(zi – z̄)2 = 914.15
Step 5: Use the sample variance formula to evaluate the sample variance.
∑(zi – z̄)2 / (N – 1) = 914.15 / 11 – 1
∑(zi – z̄)2 / (N – 1) = 914.15 / 10
∑(zi – z̄)2 / (N – 1) = 91.415
Hence the sample variance of the given sample data is 91.415.
A variance calculator by calculators.tech could be used to avoid time-consuming calculations of variance.
Example 2: For Population Data
Evaluate the average of the squared deviations from the given population data.
Population data = 9, 11, 13, 15, 14, 16, 18, 23, 26, 28, 30
Solution –
Step 1: First of all, find the population average value by taking the quotient of the sum of observations and the total number of data values.
Sum of population data = 9 + 11 + 13 + 15 + 14 + 16 + 18 + 23 + 26 + 28 + 30
Sum = 203
Total number of observation = N = 11
Population Mean = µ = 203/11
Population Mean = µ = 18.455
Step 2: Now find the deviation (difference of each data value from the average).
| Data values | yi – µ |
| 9 | 9 – 18.455 = -9.45 |
| 11 | 11 – 18.455 = -7.45 |
| 13 | 13 – 18.455 = -5.45 |
| 15 | 15 – 18.455 = -3.45 |
| 14 | 14 – 18.455 = -4.45 |
| 16 | 16 – 18.455 = -2.45 |
| 18 | 18 – 18.455 = =0.45 |
| 23 | 23 – 18.455 = 4.55 |
| 26 | 26 – 18.455 = 7.55 |
| 28 | 28 – 18.455 = 9.55 |
| 30 | 30 – 18.455 = 11.55 |
Step 3: Now take the square of the deviations to make all the results positive.
| (yi – µ)2 |
| (-9.45)2 = 89.30 |
| (-7.45)2 = 55.50 |
| (-5.45)2 = 29.70 |
| (-3.45)2 = 11.90 |
| (-4.45)2 = 19.80 |
| (-2.45)2 = 6.00 |
| (=0.45)2 = 0.20 |
| (4.55)2 = 20.70 |
| (7.55)2 = 57.00 |
| (9.55)2 = 91.20 |
| (11.55)2 = 133.40 |
Step 4: Now take the sum of the squared deviations.
∑(zi – µ)2 = 89.30 + 55.50 + 29.70 + 11.90 + 19.80 + 6 + 0.20 + 20.70 + 57 + 91.20 + 133.40
∑(zi – µ)2 = 514.7
Step 5: Use the population variance formula to evaluate the population variance.
∑(zi – µ)2 / N = 514.7 / 11
∑(zi – µ)2 / N = 46.793
Sum Up
The variance is a measure of the variability of the given sample and population data values from the expected values. You have to evaluate the mean, the difference of the data values from the mean, the square of differences, the sum of squared deviation, and the average of the squared deviations to determine the sample or population variance.














































































































































