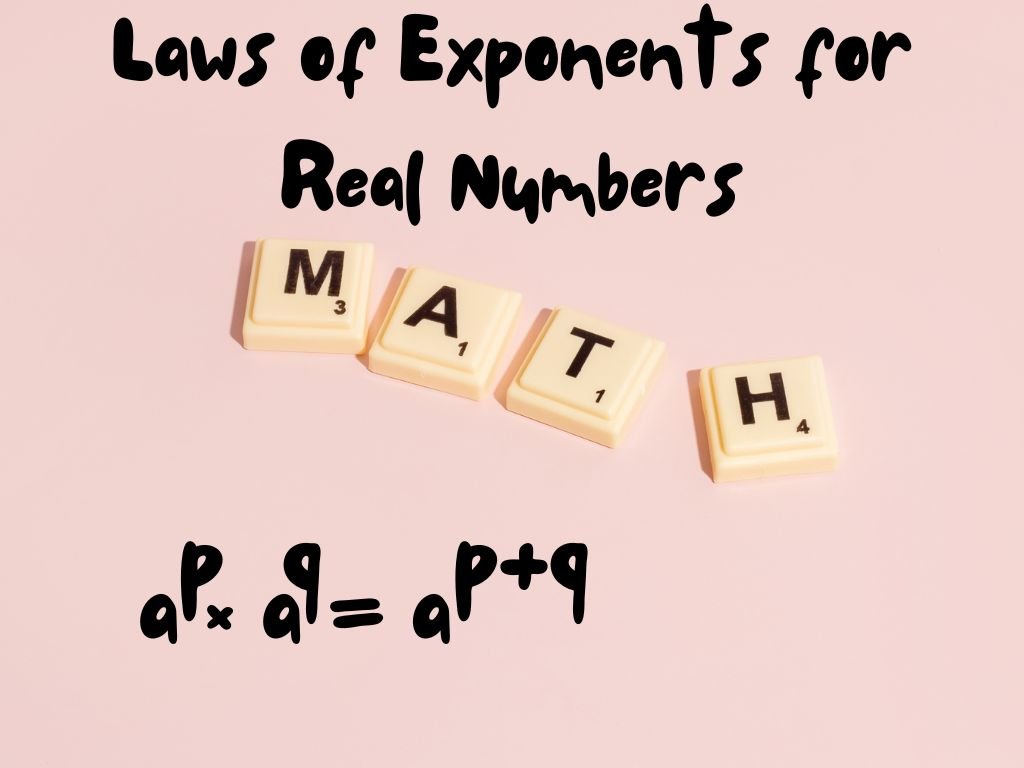When we multiply a number continuously by itself till a certain number, then exponents are used to write these numbers in a suitable and convenient form. In mathematics, we use different laws of exponents to solve large calculations. In this section, we will study different laws of exponents for real numbers.
Before understanding the laws of exponents for real numbers, let’s have a look at the laws of exponents for natural numbers. This will help us understand the difference between the two.
Laws of Exponents for Natural Numbers
Here are some laws of exponents for natural numbers as follows:
| (1) am × an = am+n | (5) am / an = am ÷ an = am-n ; m > n |
| (2) (am)n = amn | (6) am × bm = (ab)m |
| (3) a0 = 1 | (7) am / bm = am ÷ bm = (a/b)m |
| (4) if am = an then m = n | (8) am = 1 / a-m or 1 / am = a-m |
In the above laws, a, m, and n are natural numbers. a is called the base and m and n are called exponents.
Examples –
Simplify the following expressions:
(1) 125 . 123
(2) 54 / 52
(3) (206)7
(4) If 458 = 45x, then find the value of x?
(5) 29 × 99
(6) 32 ÷ 82
(7) 14-7 × 143
Solution – (1) 125 . 123
125+3 = 128
(2) 54 / 52
54-2 = 52
(3) (206)7
206×7 = 2042
(4) 458 = 45x
8 = x
x = 8
(5) 29 × 99
(2×9)9 = 189
(6) 32 ÷ 82
32 / 82
(3/8)2
(7) 14-7 × 143
14-7+3
14-4
1/144 Ans.
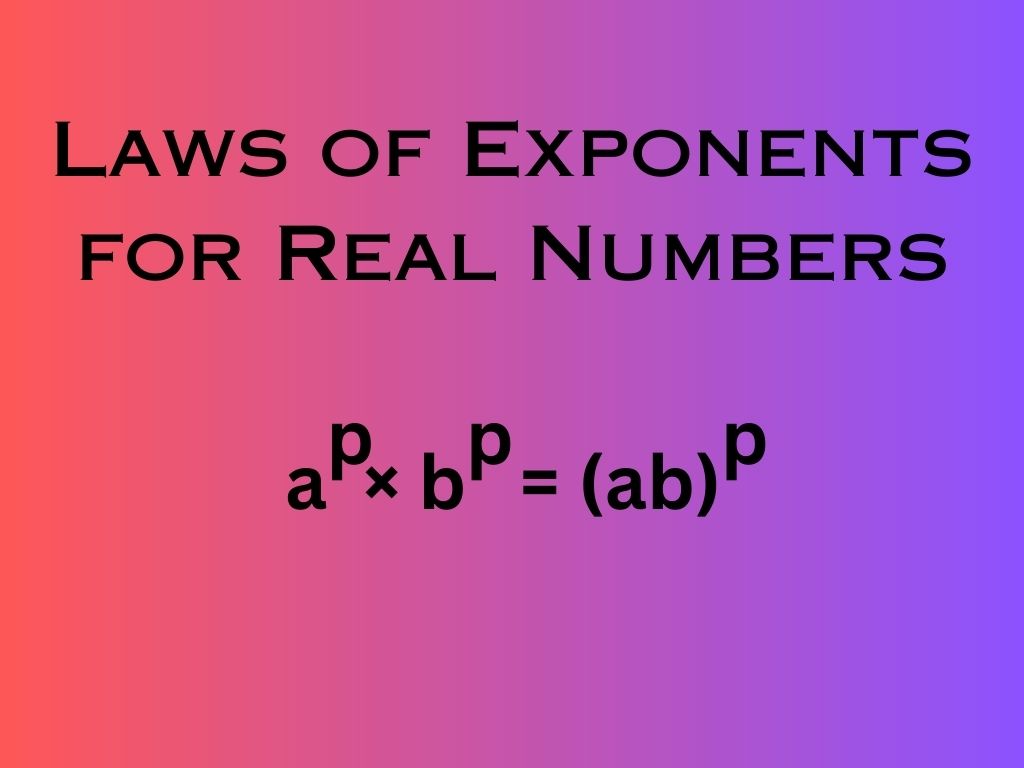
Laws of Exponents for Real Numbers
In the exponents, if the base is a positive real number and the exponents are rational numbers then how will we solve these types of questions? Let us understand with the help of some examples but before this, we understand the difference between the nth roots of square roots and exponents to understand it clearly.
According to the definition of nth roots of square roots, if a is a real number such that a > 0 and n is a positive integer.
Then, n√a = b
Or we can write, bn = a and b > 0.
According to the rules of exponents,
We define n√a = a1/n
So, for 3√5, 3√5 = 51/3
If we take 82/3 as an example, then we have two ways to solve it.
82/3 = (81/3)2 = 22 = 4
82/3 = (82)1/3 = 641/3 = 4
Therefore, with the help of the above example, we can define it as follows:
Let a be a real number such that a > 0. Let m and n be integers such that m and n have no common factors other than 1, and n > 0. Then,
am/n = (n√a)m = n√am
Now, here are some extended laws of exponents for real numbers:
Let a be a real number such that a > 0 and p and q be rational numbers. Then
| (1) ap × aq = ap+q | (5) ap / aq = ap ÷ aq = ap-q ; p > q |
| (2) (ap)q = apq | (6) ap × bp = (ab)p |
| (3) a0 = 1 | (7) ap / bp = ap ÷ bp = (a/b)p |
| (4) if ap = aq then p = q | (8) ap = 1 / a-p or 1 / ap = a-p |
Examples –
Simplify:
(1) 193/4 . 191/4
(2) 32/5 / 31/3
(3) (21/7)7/4
(4) If 258/9 = 251/x, then find the value of x?
(5) 121/5 × 21/5
(6) 232/3 ÷ 182/3
(7) 4-5/7 × 43/5
Solution – (1) 19¾ . 19¼
Using the law, ap × aq = ap+q
19(¾ + ¼) = 19(3+1 / 4) = 194/4 = 191 = 19
(2) 32/5 / 31/3
Using the law, ap / aq = ap ÷ aq = ap-q ; p > q
3(2/5 – 1/3) = 3(6 – 5 / 15) = 31/15
(3) (21/7)7/4
Using the law, (ap)q = apq
21/7 × 7/4 = 21/4
(4) If 258/9 = 251/x, then find the value of x?
Using the law, if ap = aq then p = q
8/9 = 1/x
9/8 = x/1
x = 9/8
(5) 121/5 × 21/5
Using the law, ap × bp = (ab)p
(12×2)1/5 = 241/5
(6) 232/3 ÷ 182/3
Using the law, ap / bp = ap ÷ bp = (a/b)p
232/3 / 182/3
(23/18)2/3
(7) 4-5/7 × 43/5
Using the laws, ap × aq = ap+q and ap = 1 / a-p or 1 / ap = a-p
4(-5/7 × 3/5) = 4(-3/7) = 1 / 43/7 Ans.